动手学运动规划:1.5 Frenet坐标系

All tragedy erased, I see only wonders. 我忘却了所有的悲剧，所见皆是奇迹。

—Hollow Knight 空洞骑士

🏰代码及环境配置：请参考0.2 环境配置和代码运行 | 动手学运动规划!

---

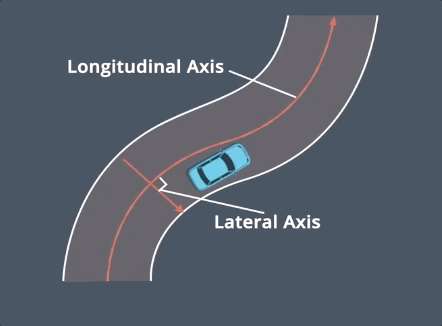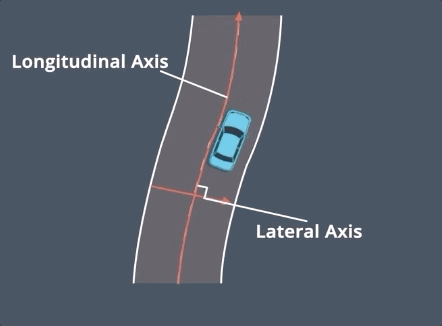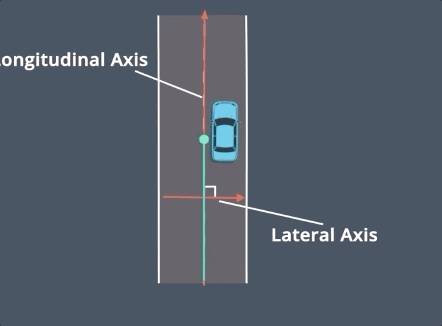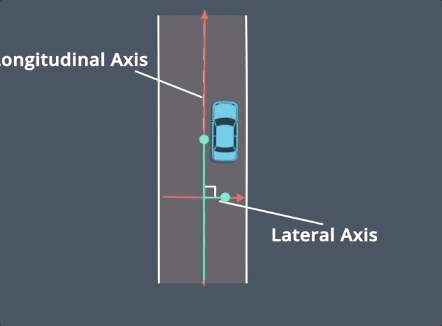
Frenet坐标系是一种在几何学和物理学中常用的坐标系，特别是在轨迹规划和机器人控制中，它能够更直观地表示车辆在弯曲道路上的位置。

1.5.1 概念与优点

通常情况下我们会使用笛卡尔坐标系描述物体的位置，但笛卡尔坐标系对车辆来说信息并不直观，即使给出了车辆位置(x,y). 比如说我们很难直接根据道路边界,其他车辆的(x,y)坐标快速确定对方与自车的相对位置关系.

为了对这些问题进行简化, 在规划算法中经常使用到Frenet坐标系坐标系:

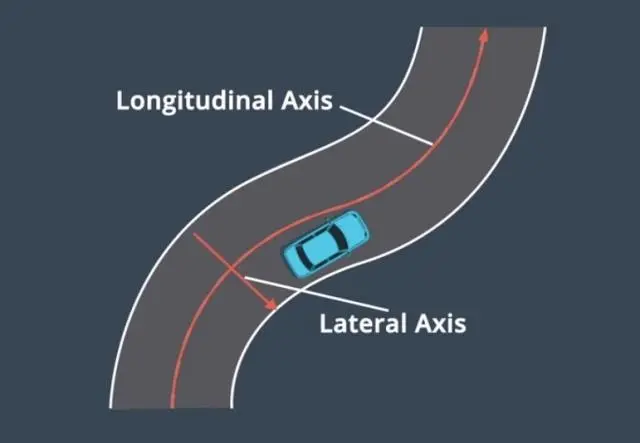
在Frenet坐标系中，车辆的位置由两个坐标描述：s和d。它将道路中心线作为参考线, s表示沿道路的纵向位移，即从道路起点到车辆当前位置的曲线距离；d表示横向位移，即车辆质心到道路中心线的法向距离。

这样做的好处有:

• 直观表达：Frenet坐标系能够直观表达车辆在道路上的行驶距离和偏离中心线的距离，从而简化了对车辆运动状态的描述。
• 解耦运动：在Frenet坐标系下，车辆的运动可以分解为沿道路中心线的纵向运动和垂直于道路中心线的横向运动。这种解耦使得车辆运动的规划和控制更加简单和高效。
• 适应复杂道路：由于实际道路大多不是笔直的，Frenet坐标系能够更好地适应曲线路径，提供比笛卡尔坐标系更准确的车辆位置信息。

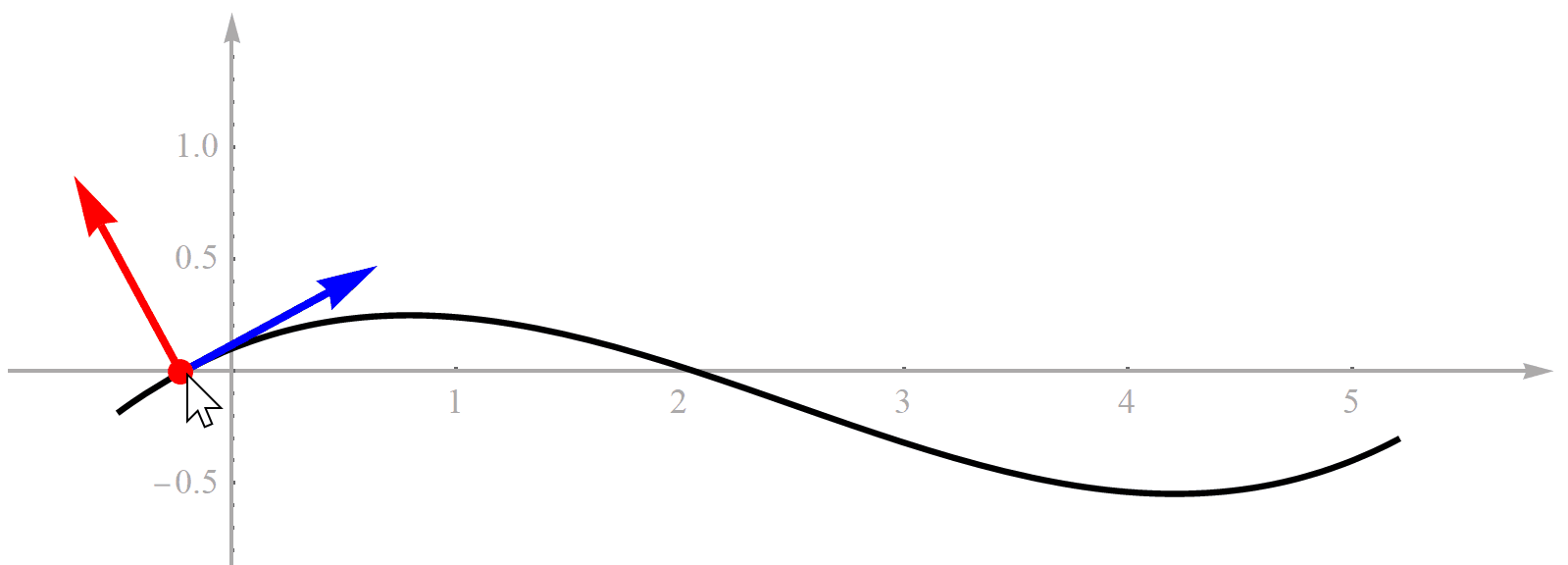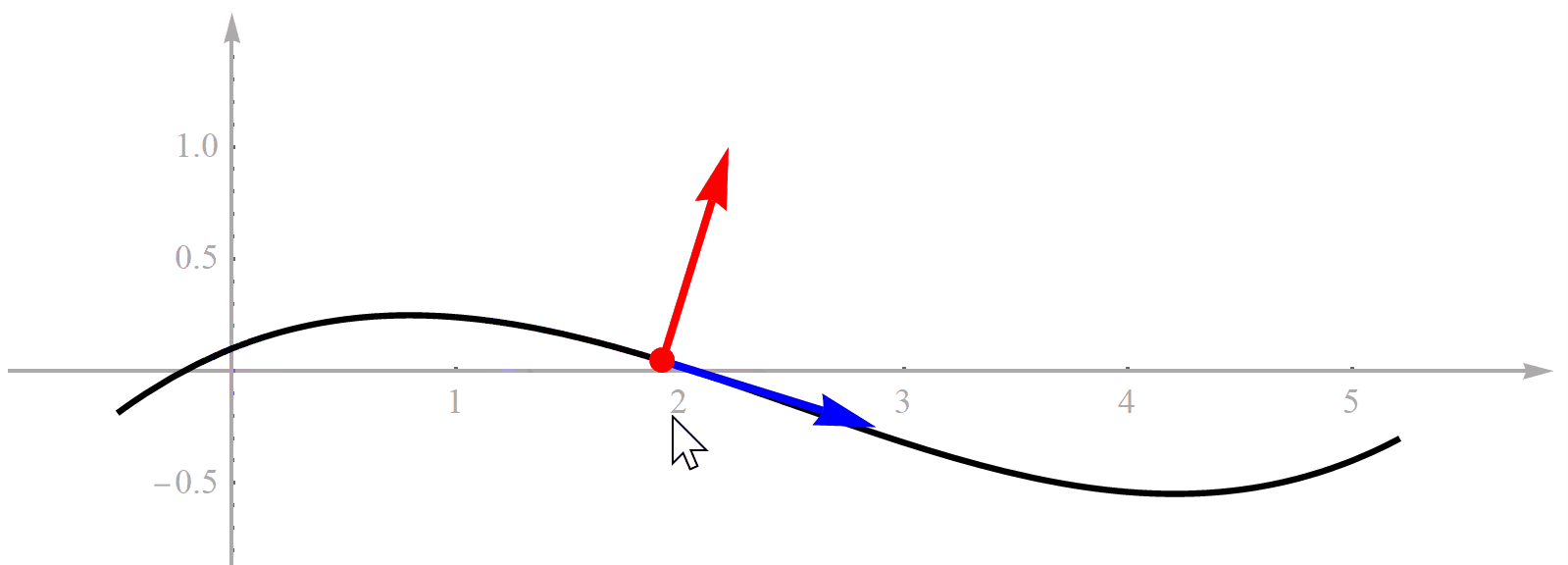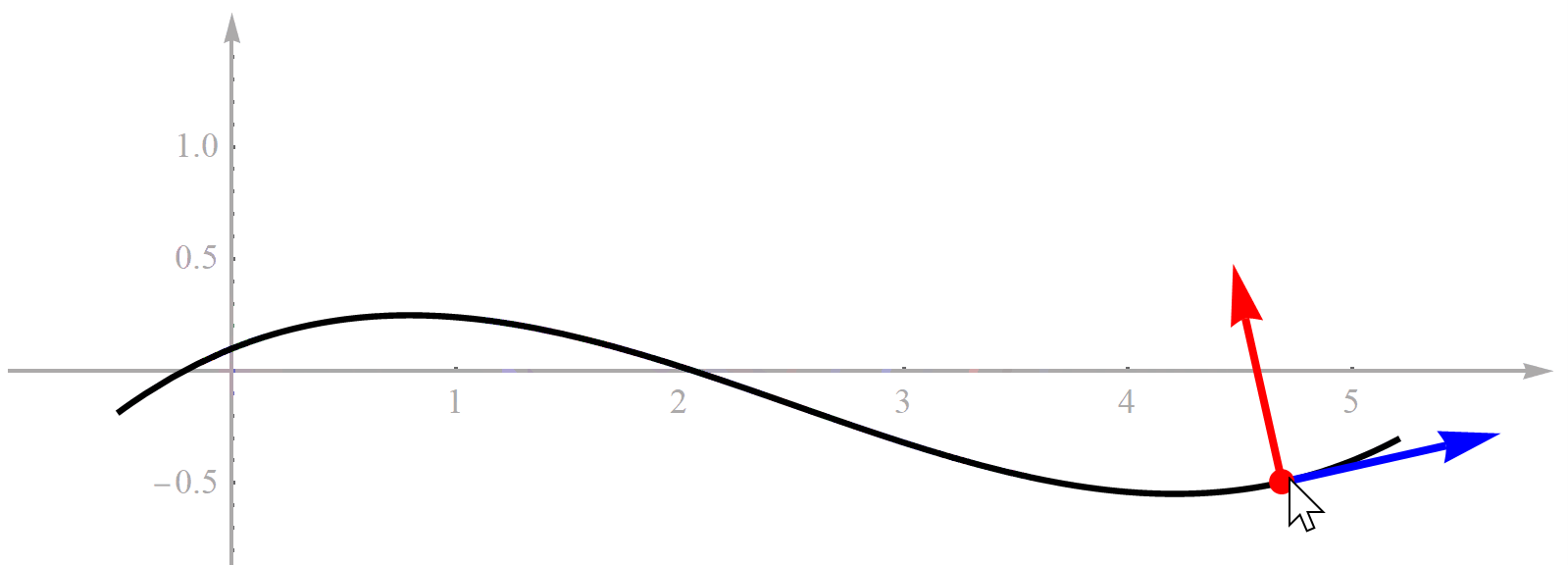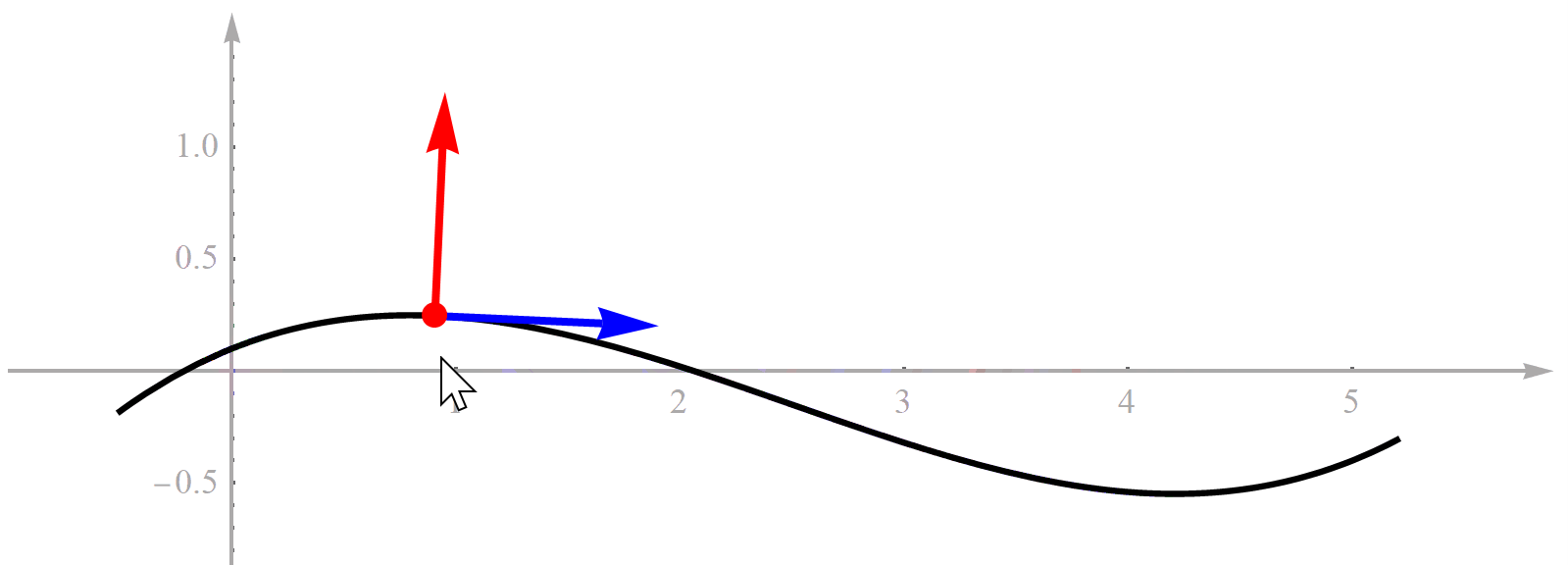
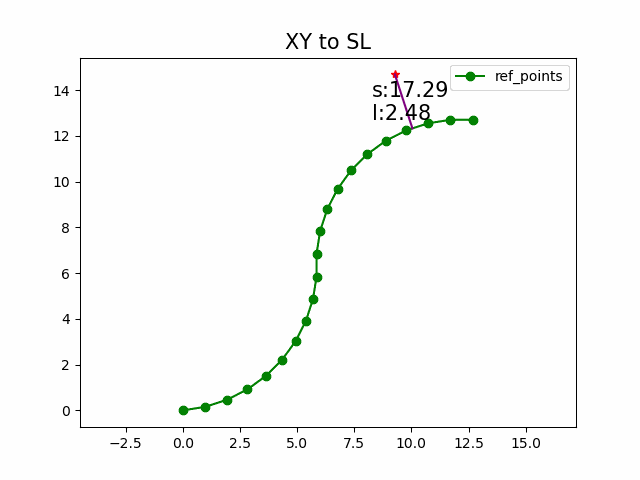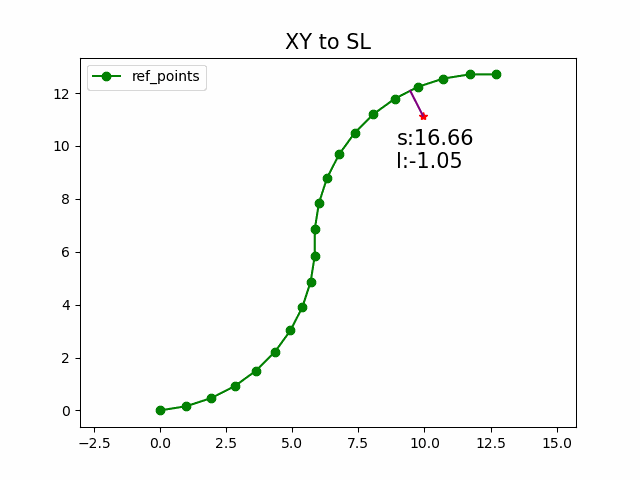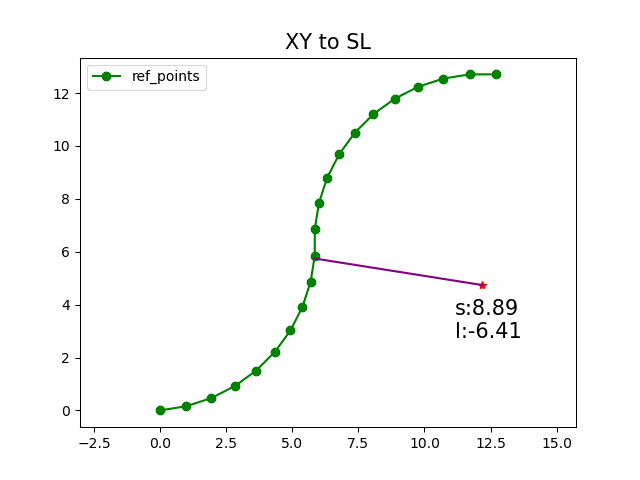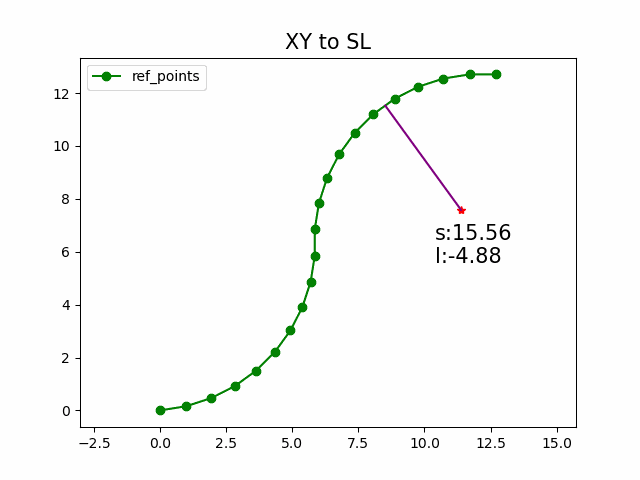
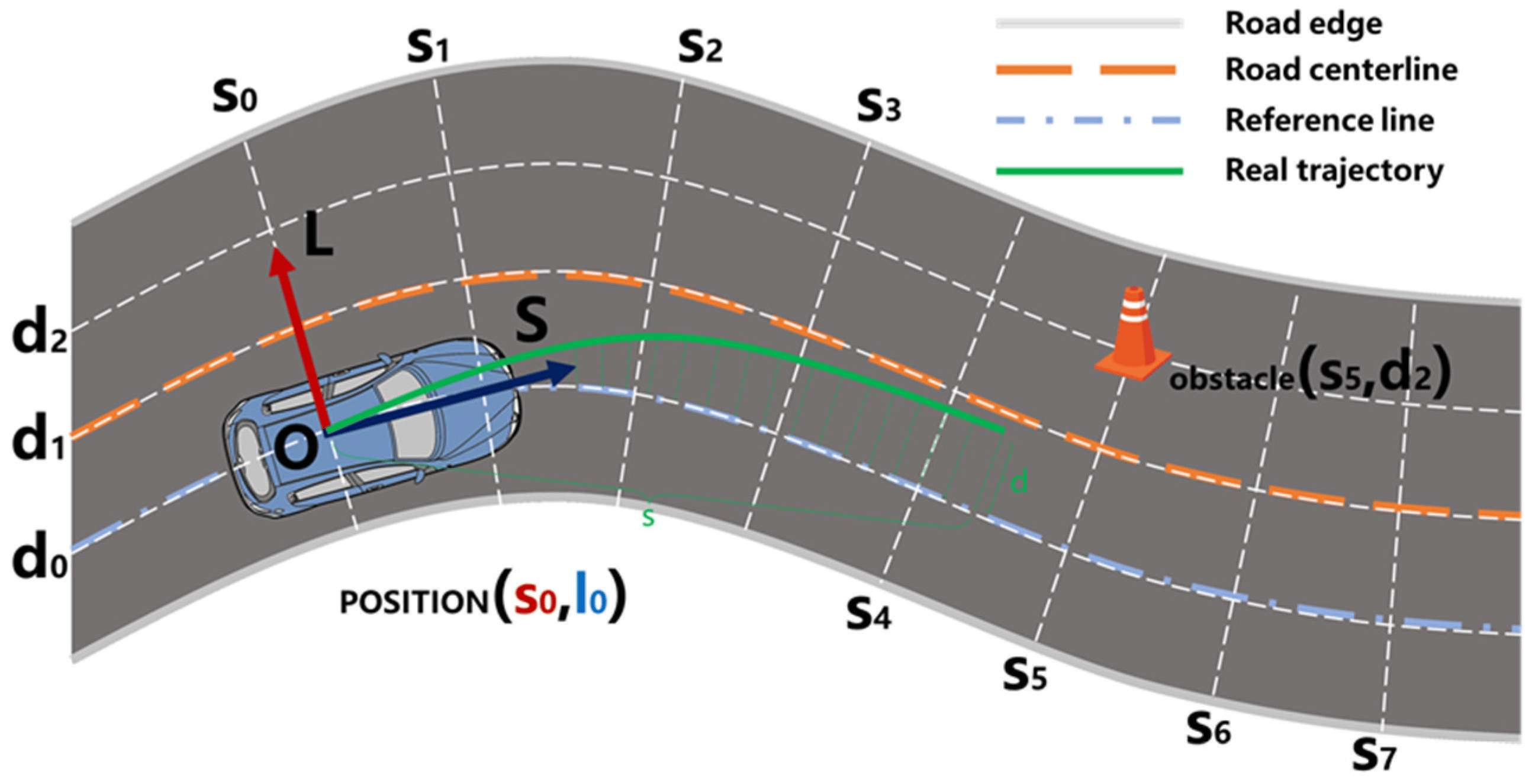
这张图形象的展示了Frenet坐标系与Cartesian 坐标系的关系. 正是因为结构化道路存在一条较为清晰的参考线, 使得Frenet坐标系可以方便的应用到算法中.

1.5.2 仅需要低阶信息的坐标转换

在实际工程应用中,大部分场景下我们只需要获取转换后的0阶信息:(s,l). 这时可以用尽量少的计算来实现.

1.5.2.1 Cartesian$(x_p,y_p)$ → Frenet$(s_p,d_p)$

首先我们给出定义:

$$\begin{gathered} \arg \underset{s=s^{\ast }}{\min }\left|D(x_p,y_p,s)\right| \\ \Gamma =\left\{(x,y)\in {\mathbb{R}}^2\mid x=f_x(s),y=f_y(s),s.t.s\in [0,L]\right\} \end{gathered}$$

• $(x_p,y_p)$是需要转换的笛卡尔点
• $\Gamma$是一个定义在笛卡尔坐标系下的指引线,是一系列点的集合
• 指引线上的点由参数化方程$f_x(s),f_y(s)$确定
• s是以指引线起点为原点的累积长度,
• L是指引线的总长度
• $D(s)$是点$(x_p,y_p)$$(x_p,y_p)$$[x(s),y(s)]$处的法向投影长度

那么问题就是找到使得法向投影最短的指引线上的点$(x(s^{\ast }),y(s^{\ast }))$. $s^{\ast }$就是转换后Frenet坐标系的$s_p$, $D(x_p,y_p,s^{\ast })$就是Frenet坐标系的$l_p$.

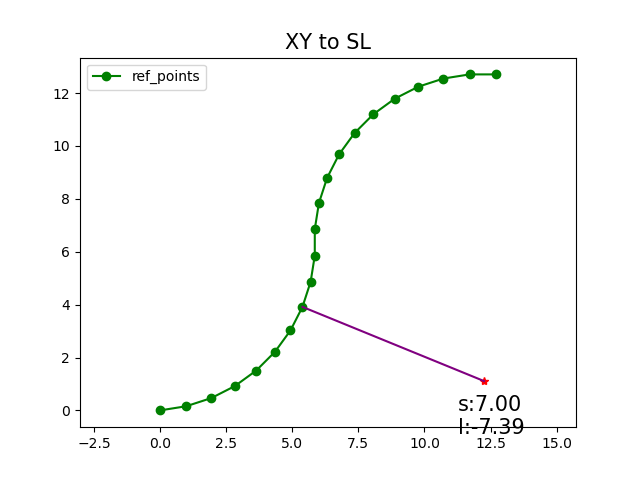
由于无法保证指引线与$(x_p,y_p)$的相对位置关系, 所以这个问题大概率是非凸的. 在工程上, 指引线可能不是一条连续的样条, 也可能是一系列的离散点. 一般采取暴力遍历或者是增加一些剪枝来减少计算. 但是总的来说, 为了确定能够准确转换的(s,d), 需要计算出全局最优解.

遍历或者采样指引线上的点, 间隔越短精度越高. 使用向量的叉积即可快速计算$D(x_p,y_p,s)$, 从而计算出坐标转换结果$(s,d)$

1.5.2.2 Frenet$(s_p,d_p)$ → Cartesian$(x_p,y_p)$

Frenet向笛卡尔坐标系转换则简单的多, 只需要在指引线上获取$(x_s,y_s)$坐标之后, 在该点的法向(根据d的方向决定顺时针法向还是逆时针法向)上, 延长$d_p$距离即可

$$(x_p$$