线性代数自学——俗说矩阵

文章内容：4-初识矩阵的秩_哔哩哔哩_bilibili

俗说矩阵：B站最宝藏的线性代数视频系列！一学就懂！_哔哩哔哩_bilibili

目录

一、初识矩阵的秩

1.上一章回顾

(1)线性方程组及其矩阵表示

(2)线性方程组的解

(3)如何判断线性方程组解的类型

2.秩（r(A)的本质含义）

r(A)=0的矩阵

r(A)=1的矩阵

特殊情况

五、矩阵求解线性方程组举例

例1

例2

---

一、初识矩阵的秩

1.上一章回顾

(1)线性方程组及其矩阵表示

(2)线性方程组的解

(3)如何判断线性方程组解的类型

2.秩（r(A)的本质含义）

(1)对于矩阵A，将其经过初等行变换后变为阶梯矩阵，阶梯矩阵的非零行数就是矩阵A的秩（Rank），记为r(A)。

秩的求法：

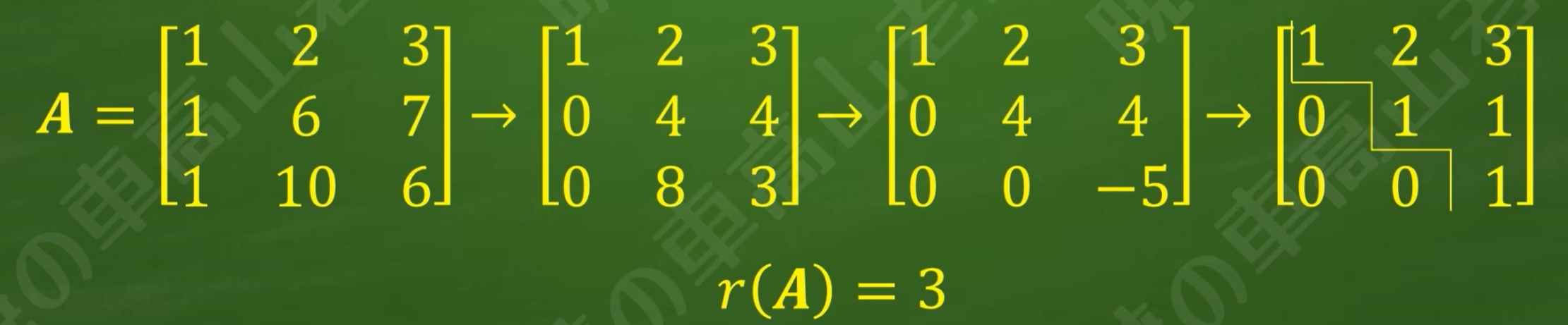
(2)矩阵初等行变换不改变矩阵的秩

(3)矩阵的秩不超过矩阵的行数，也不超过矩阵的列数

r(A)=0的矩阵

(1)如果矩阵A所有的元素都是0，则它不存在非零行，r(A)=0

(2)此时称之为零矩阵（Zero Matrix），记为A=O

(3)A=O和r(A)=0是等价关系（充要条件）

r(A)=1的矩阵

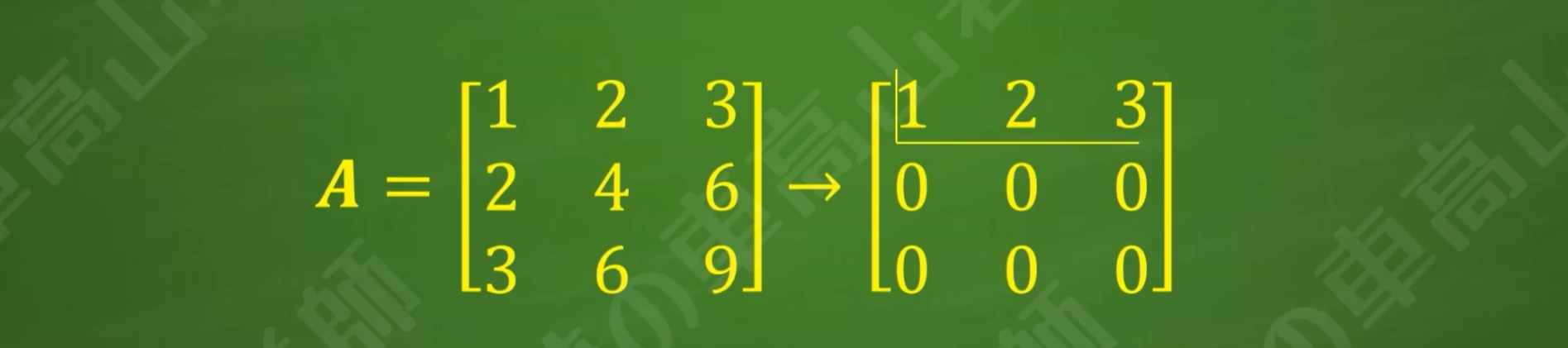
(1) r(A)=1的矩阵各行和各列成比例

(2)比例系数可以是0，且至少保证矩阵内有一个元素不为0

特殊情况

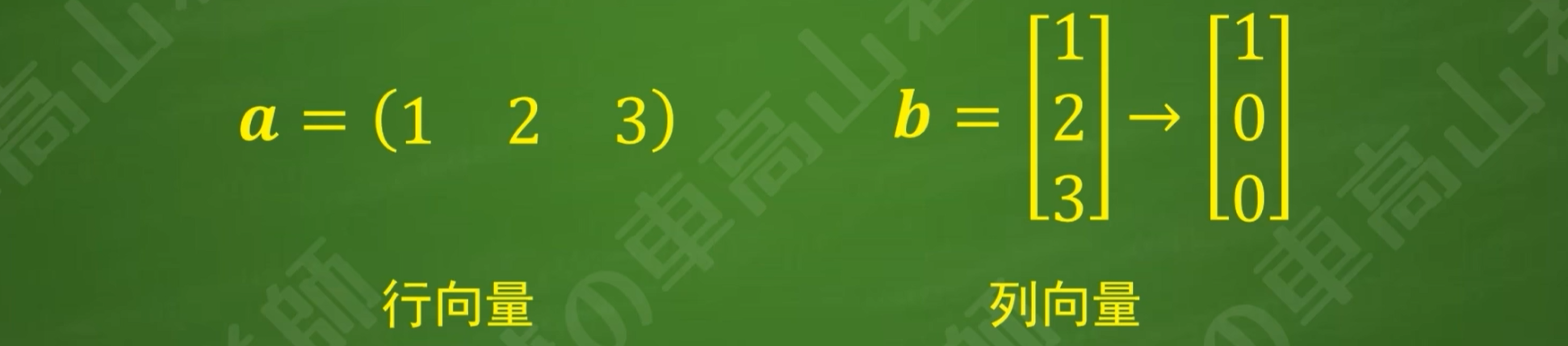
(1)向量是只有1行或只有一列的矩阵

(2)所有不为0的向量，不论行向量还是列向量，秩都是1

(3)向量a≠0和r(a)=1相互等价（充要条件）

五、矩阵求解线性方程组举例

例1

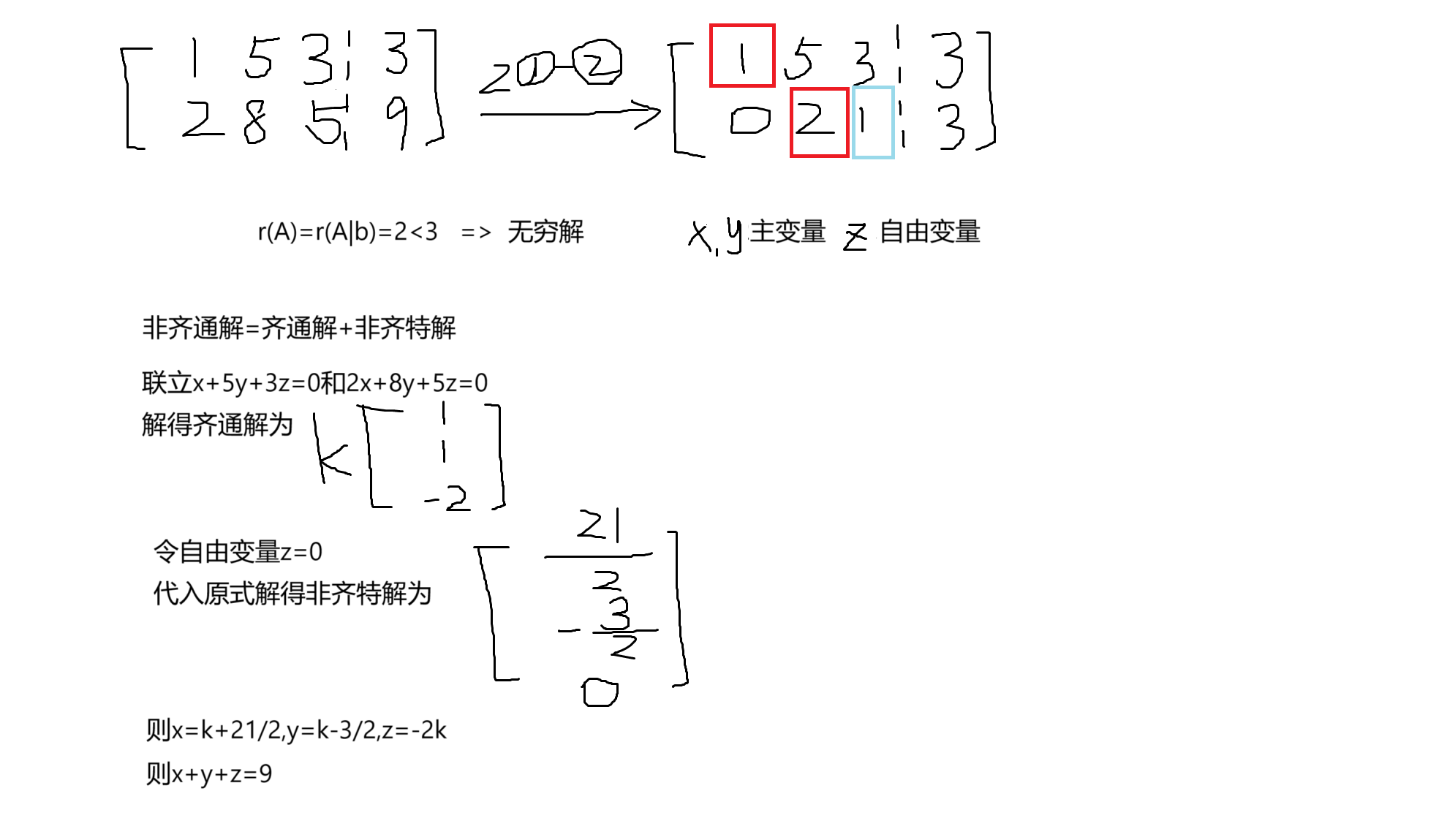
已知x+5y+3z=3,2x+8y+5z=9,求x+y+z的值

解1：（视频里给出）

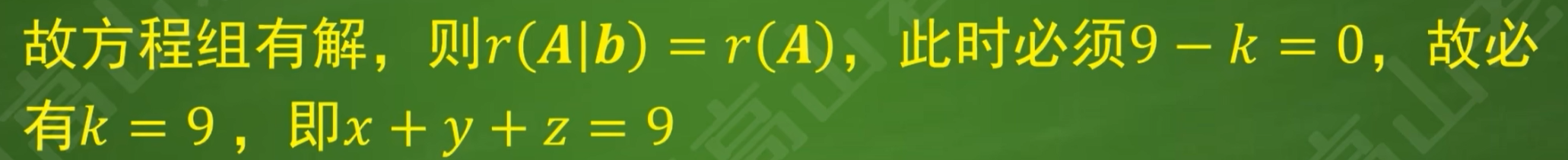
解2：（自己算的比较麻烦，有问题希望各位斧正）

例2

求证：3个不共线且横坐标两两不同的点(x1,y1),(x2,y2),(x3,y3)可以确定唯一的二次函数y=ax²+bx+c(a≠0)

解：

注：x1,y1,x2,y2,x3,y3皆为已知，a,b,c为未知数，则关于a,b,c的三元一次方程组，三点不共线y1,y2,y3不相等，因此一定是非齐次方程组

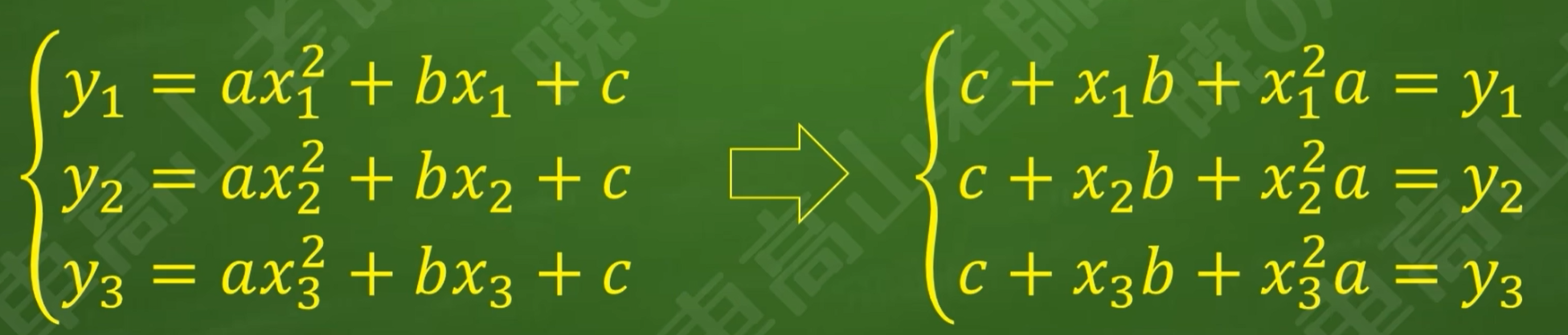
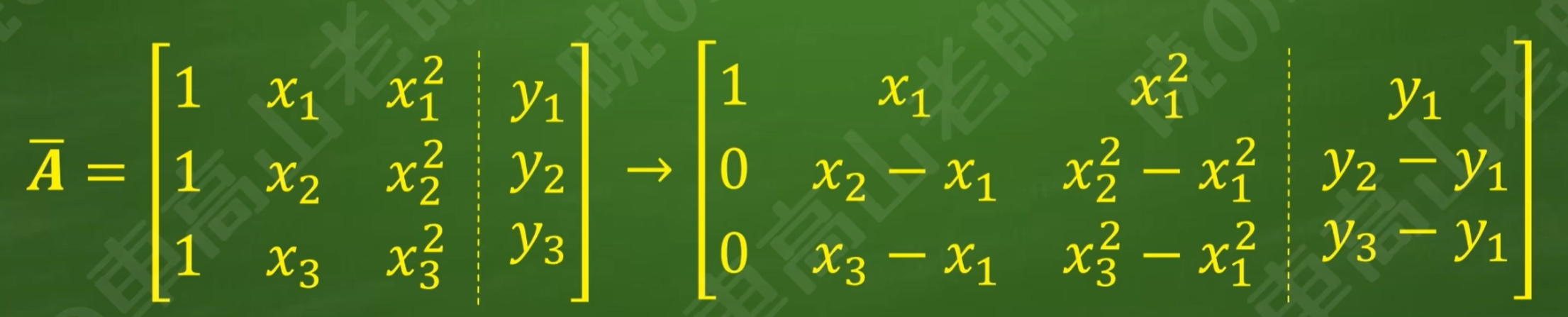
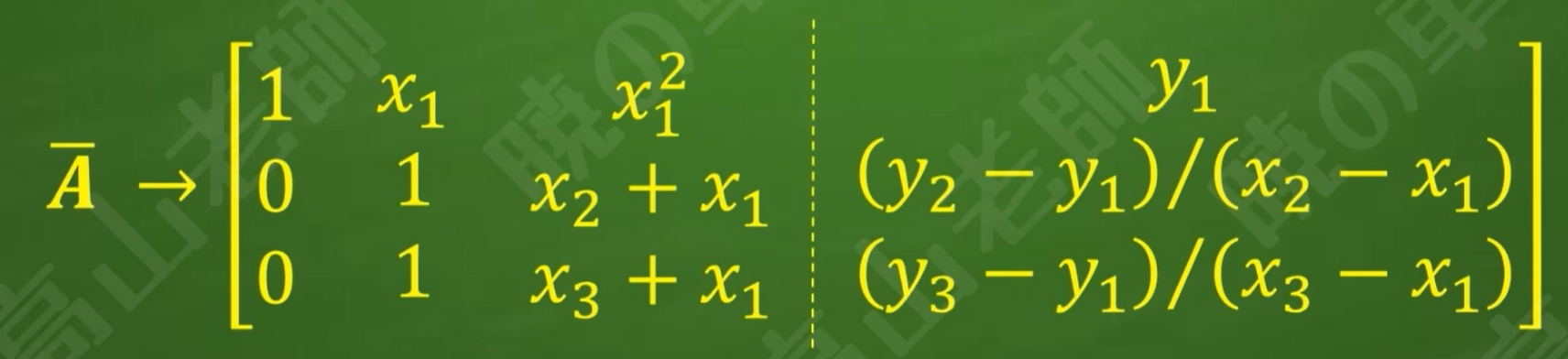
注意：a≠0

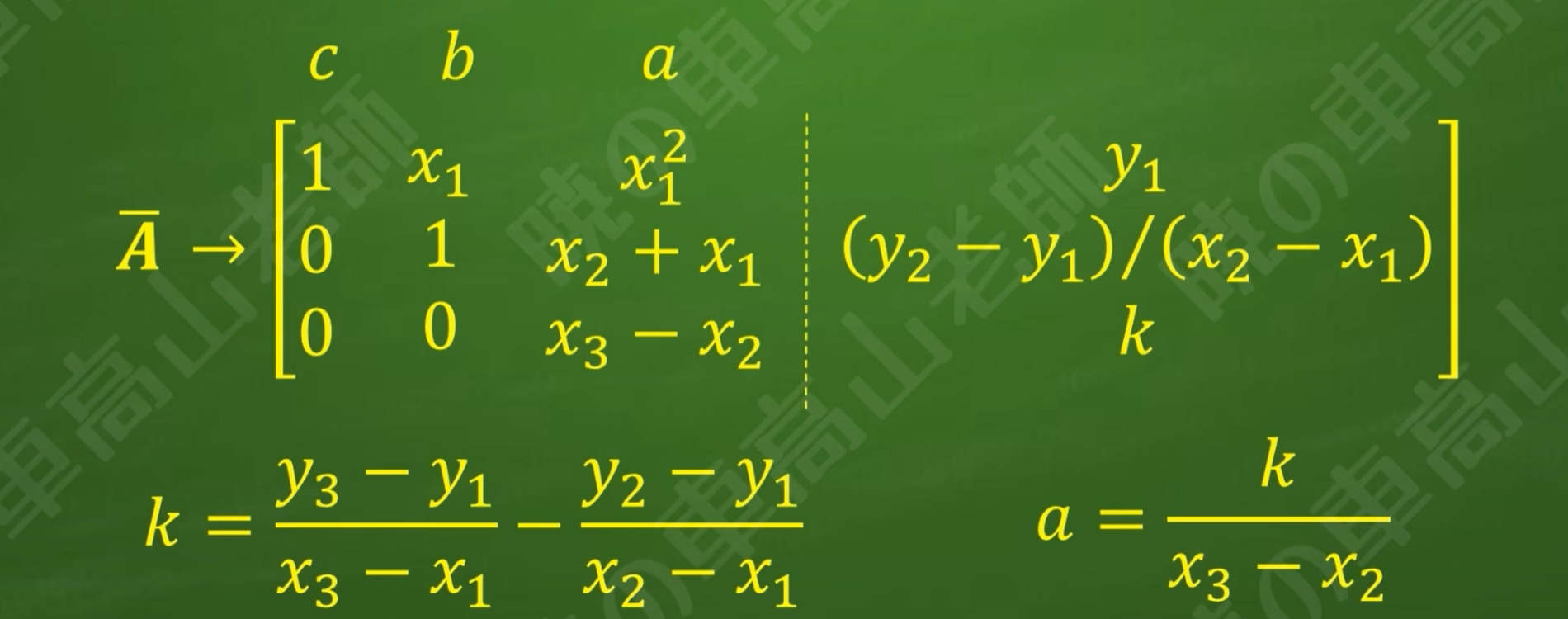
则证明k≠0

（例2作者本人需要巩固，标注一下）