文章内容参考视频:俗说矩阵:B站最宝藏的线性代数视频系列!一学就懂!-智伤帝-数学-哔哩哔哩视频
目录
一、从二元一次方程组说起
1.高斯消元法
代入消元法、加减消元法(具体例子如下)

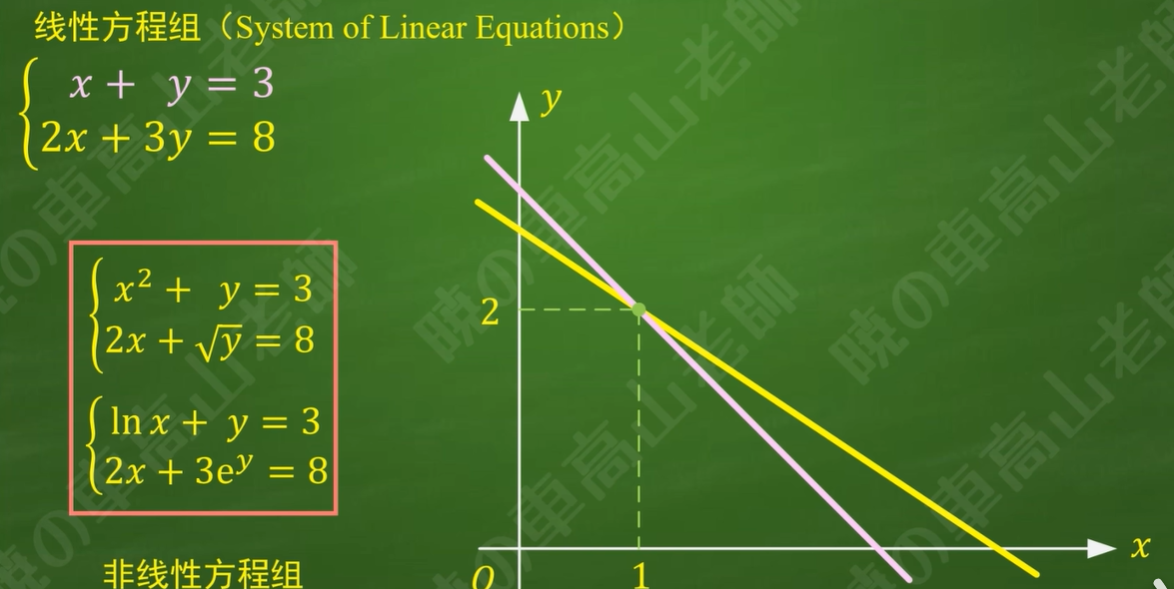
从解析几何来看,二元一次方程的本质是一条直线,对应的点为两条直线的交点
2.线性方程组
包括齐次线性方程组和非齐次线性方程组

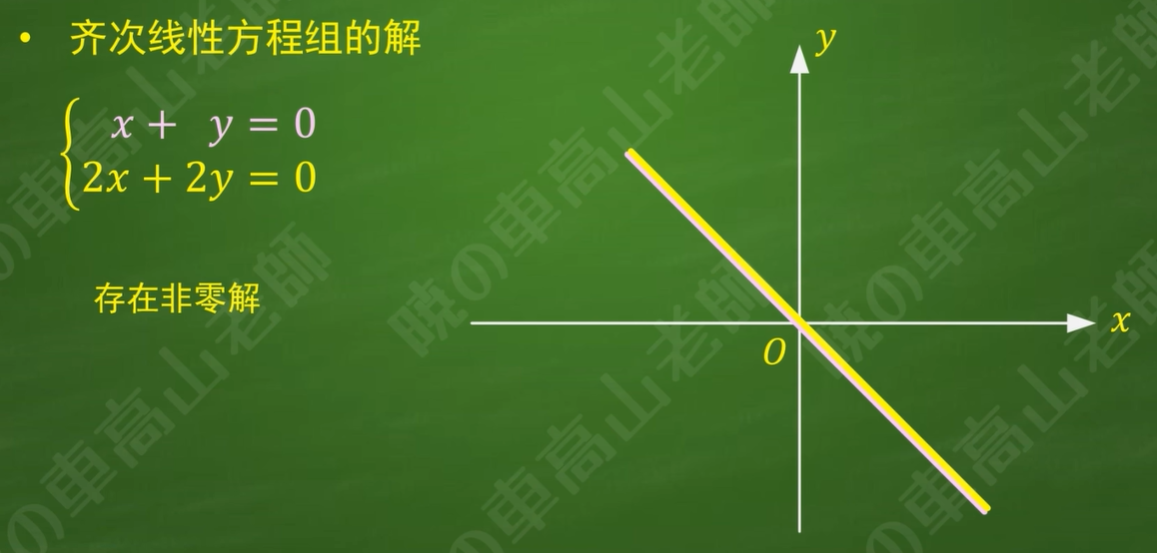
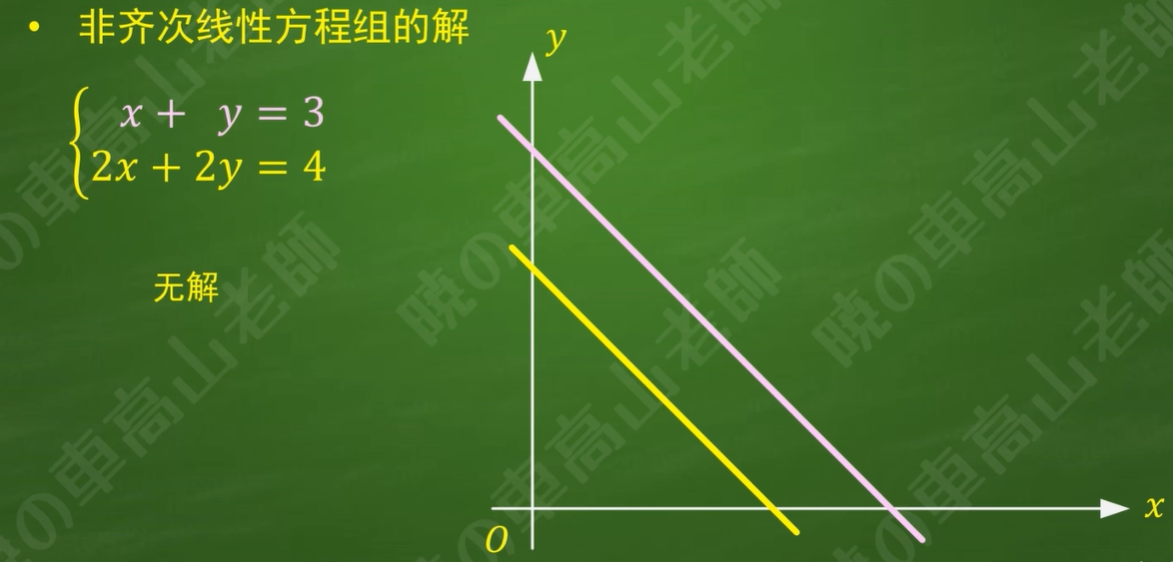
且存在无数个非零解
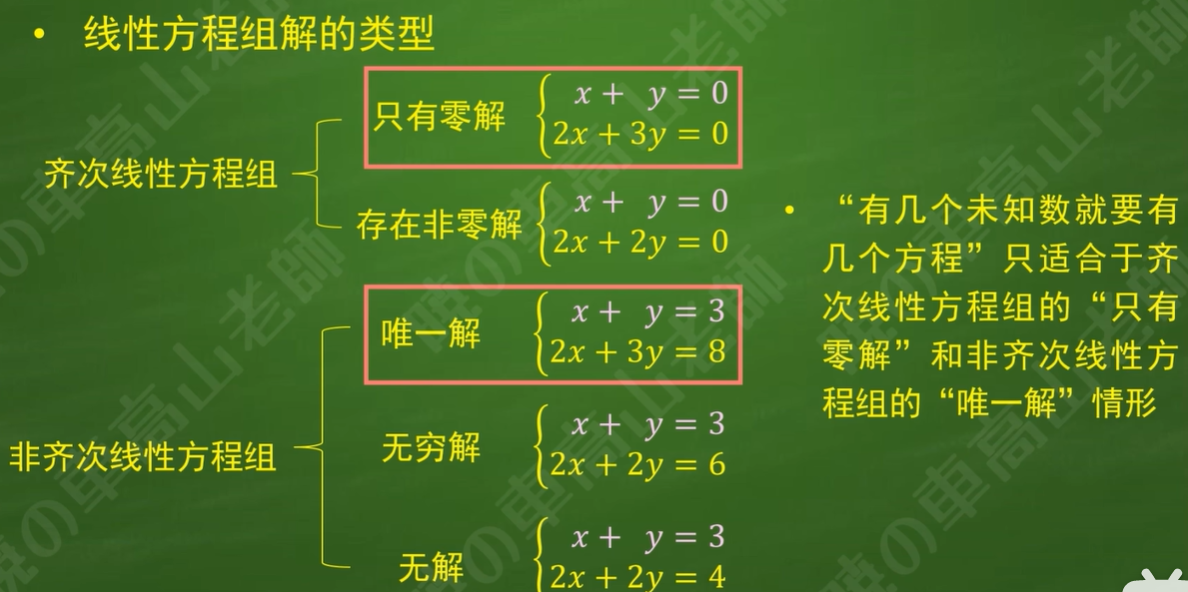
小节——线性方程组解的类型
3.齐次线性方程组的一般形式
适用于:更多的未知量、方程个数和未知量个数不一致、解方程消元没有目的性


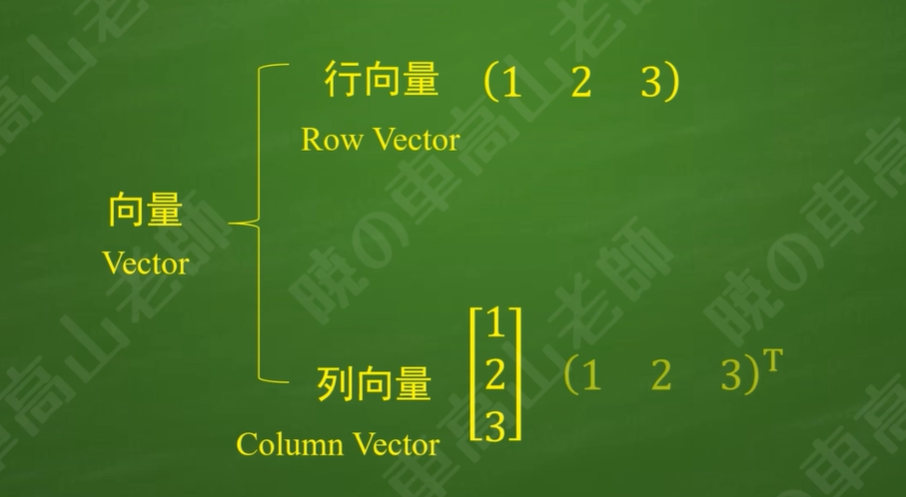
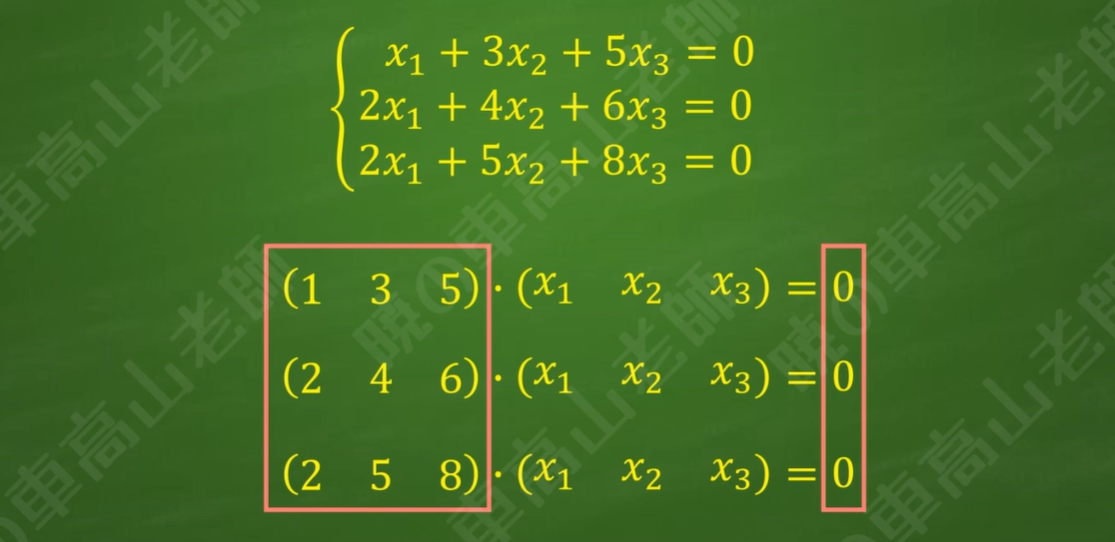


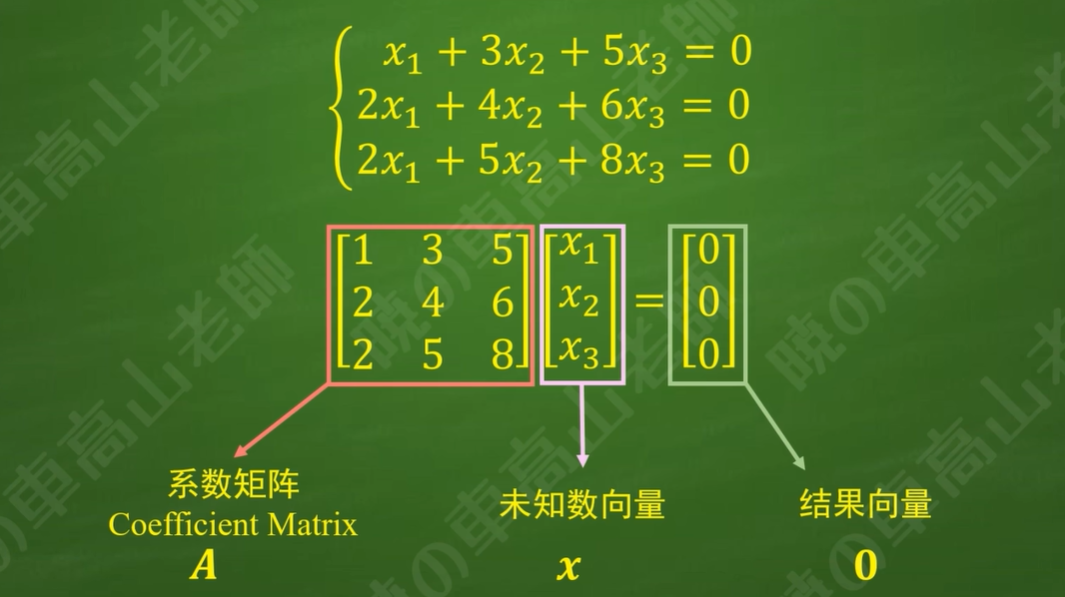

4.非齐次线性方程组的一般形式

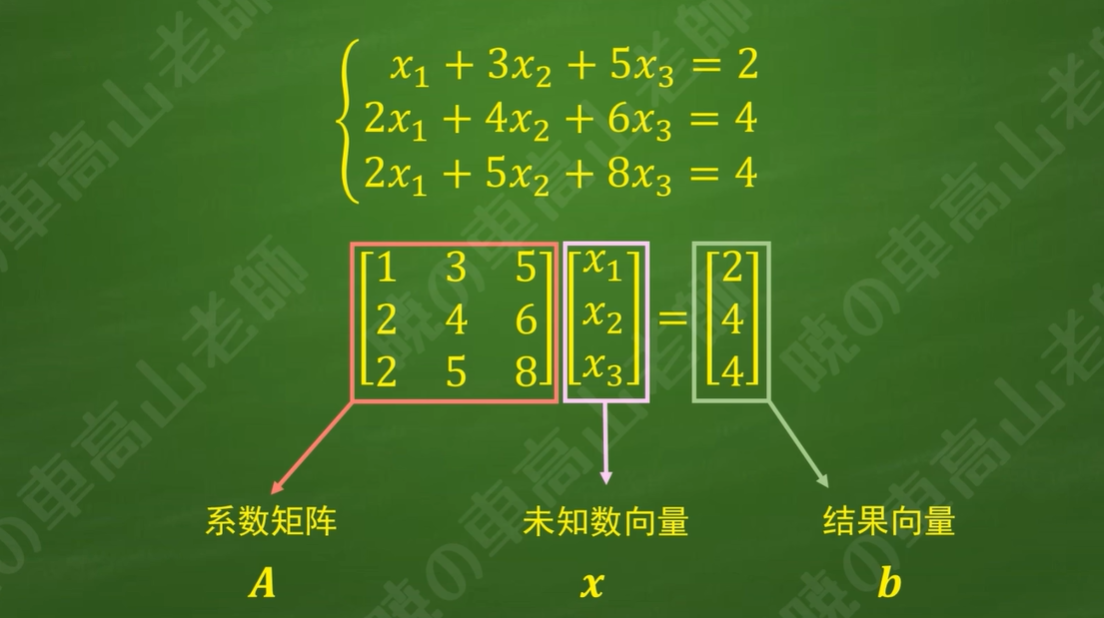

例 如何利用矩阵进行高斯消元求解
 5.矩阵初等行变换(齐次)
5.矩阵初等行变换(齐次)
1.给某行同时乘以一个非零常数k

方程有公因数
2.交换某两行的位置

3.把某一行的k倍加到另一行上

继续变换:

阶梯矩阵

将一般矩阵转化为阶梯矩阵

使得往下出现在一开始的0越多
6.非齐次方程组和增广矩阵
方程结果不全为0,因此在对方程进行约分和加减时,需要和对应结果一起运算
对应到矩阵的初等行变换,需要系数矩阵和初等行变量同步变换,将结果向量写在系数矩阵右侧,构成多一列的新矩阵,即增广矩阵


7.总结

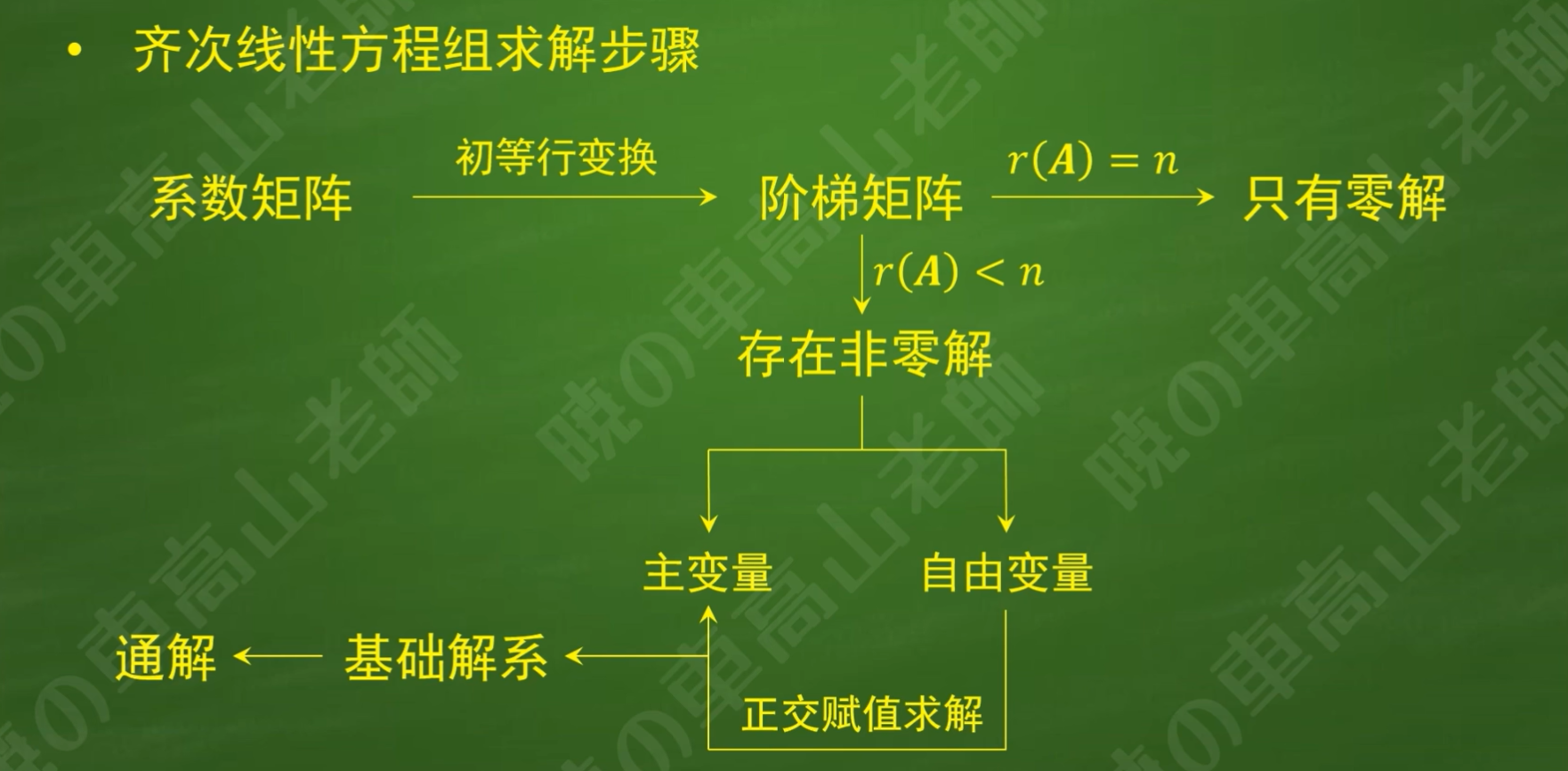
二、求解齐次线性方程组
1.上一章内容总结





2.通解
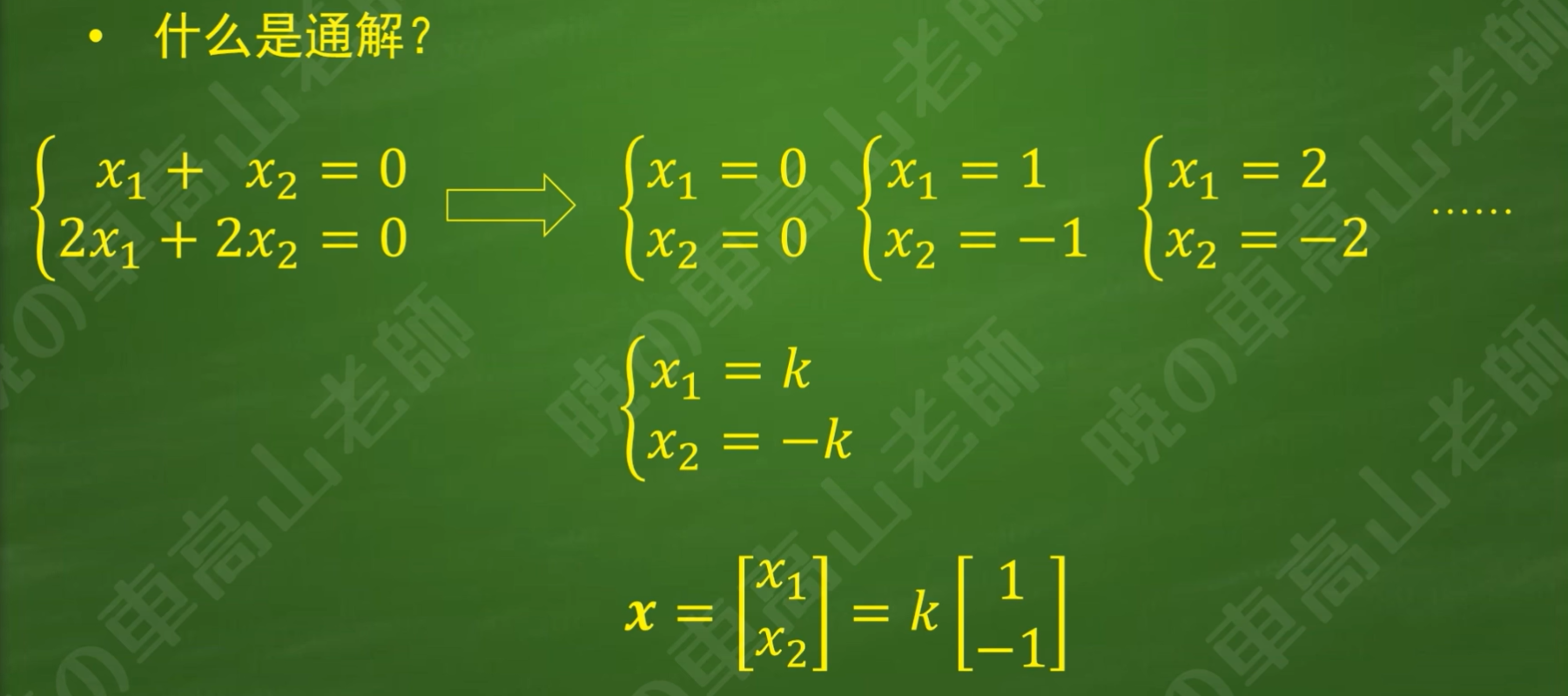

计算从下往上代入(自变量少的往自变量多的代入)
方程仅有零解,写出系数矩阵发现为阶梯矩阵(右上方元素不为0,左上角所有元素皆为0),三行皆不为0,恰好和未知数个数相同,得出结论:
阶梯系数矩阵非0行数和未知数个数相等,齐次线性方程组只有零解(行满秩矩只有零解)
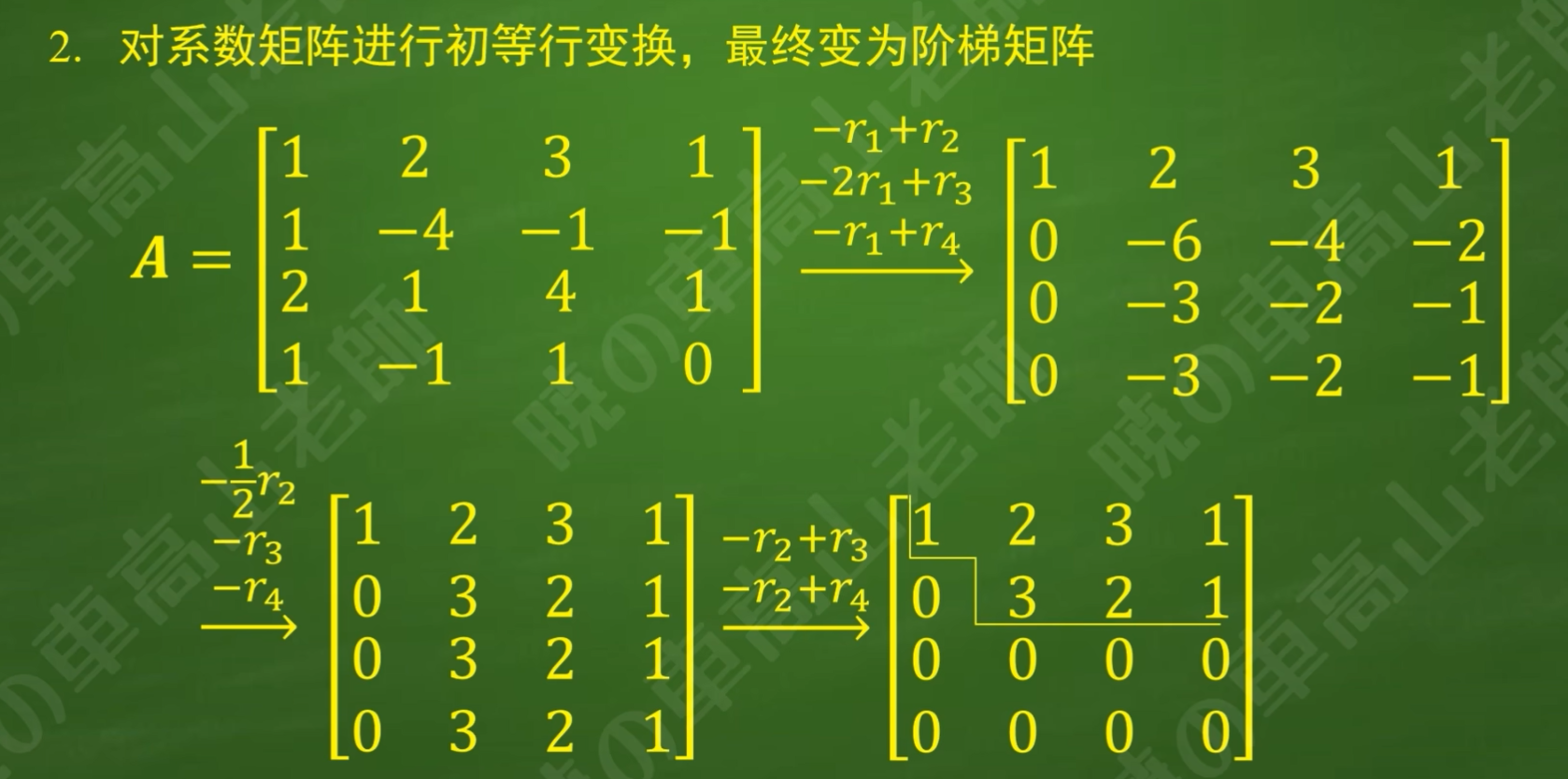
将系数矩阵转化为阶梯矩阵步骤如下:



计算步骤如下:

非零解的求法:自底向上,固定x3,将x1,x2都用x3来表示方程的解,因为任意的x3均满足方程组因此提出x3为纯数字

基础解系即为方程组通解

主变量和自由变量

红框为主变量,即阶梯矩阵最前面的系数;蓝色框为自由变量,即除主变量以外的变量
1.主变量的个数等于非零变量的行数,用r(A)来表示
2.自由变量t=n-r(A)
如果只有一个自由变量,只需给自由变量赋值一次即可
有两个自由变量,给自由变量赋值两次正交为(1,0)(0,1)


一个方程组有三个自由变量,赋值三次为(0,0,1)(0,1,0)(1,0,0)
例子



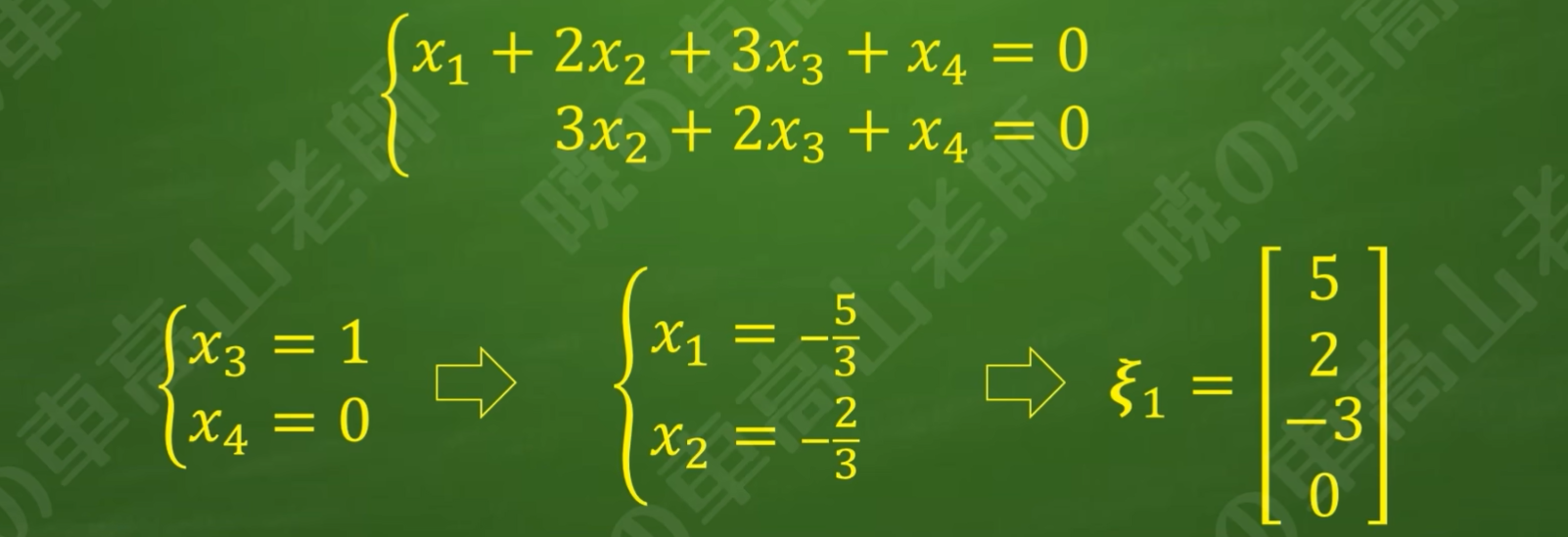
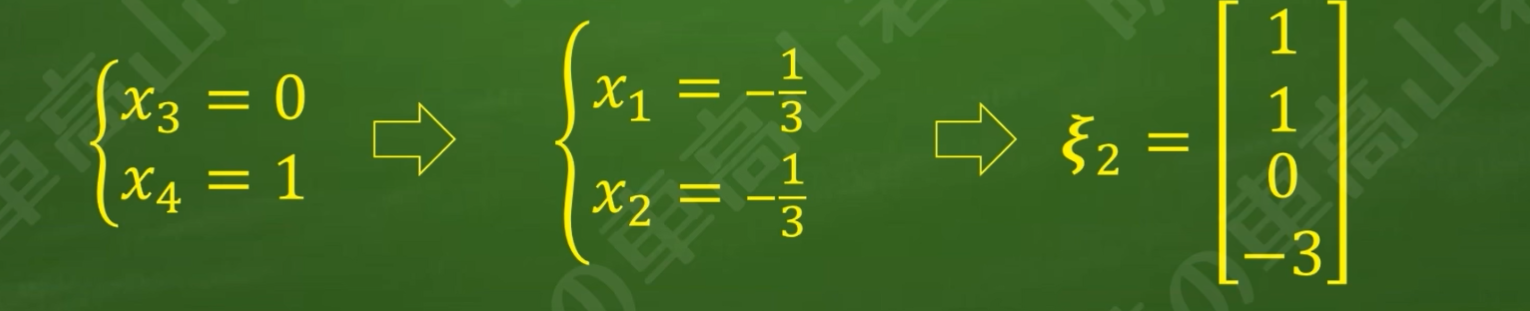

三、求解非齐次线性方程组
1.上一章内容总结
2.非齐次方程组的解
(1)唯一解
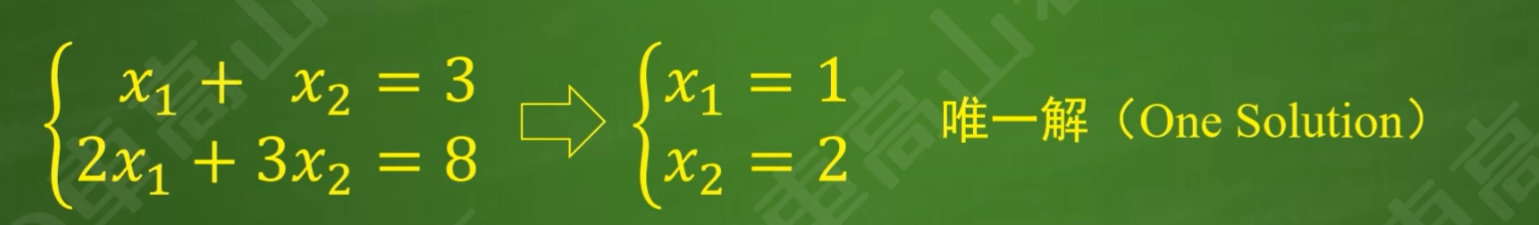
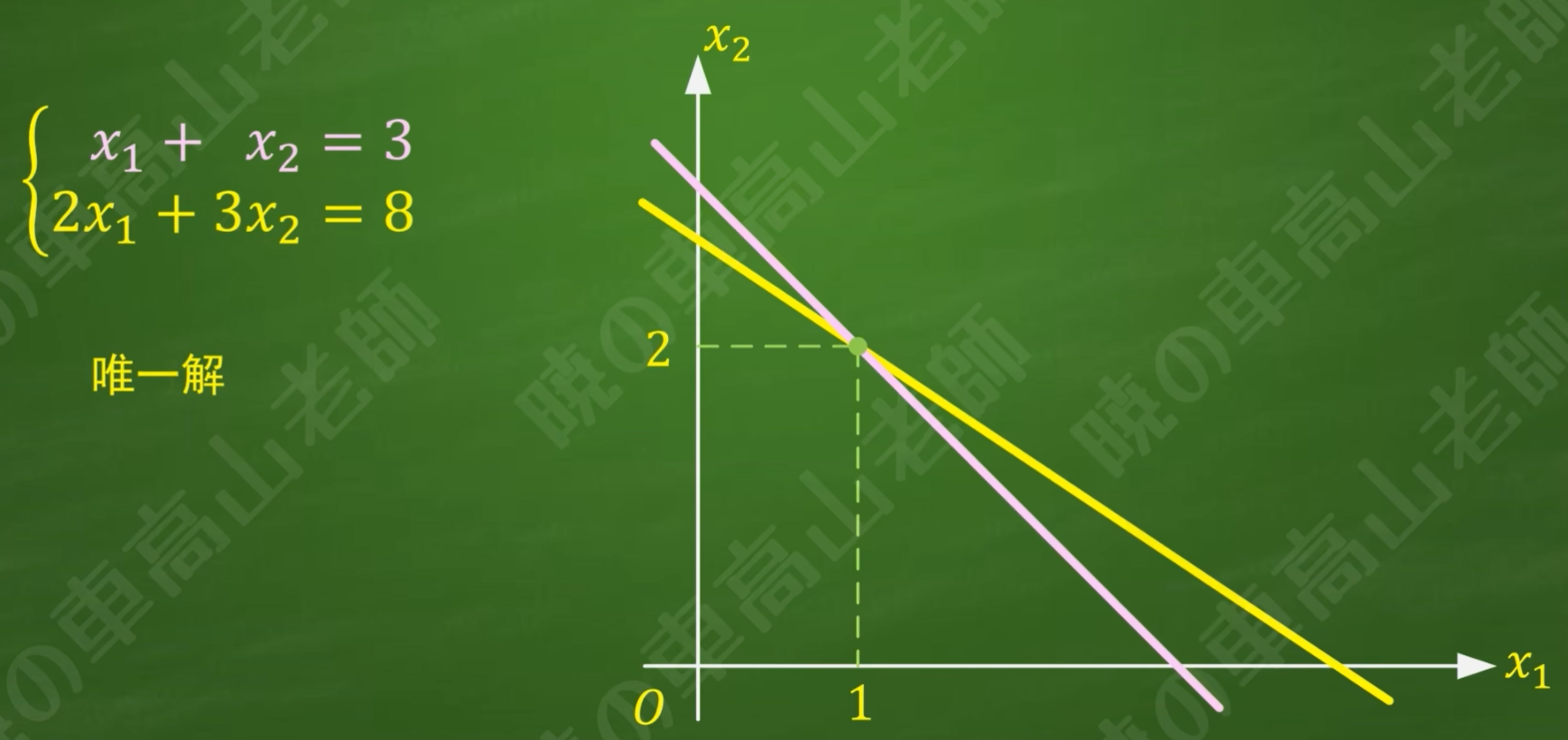
几何意义:
(2)无穷解
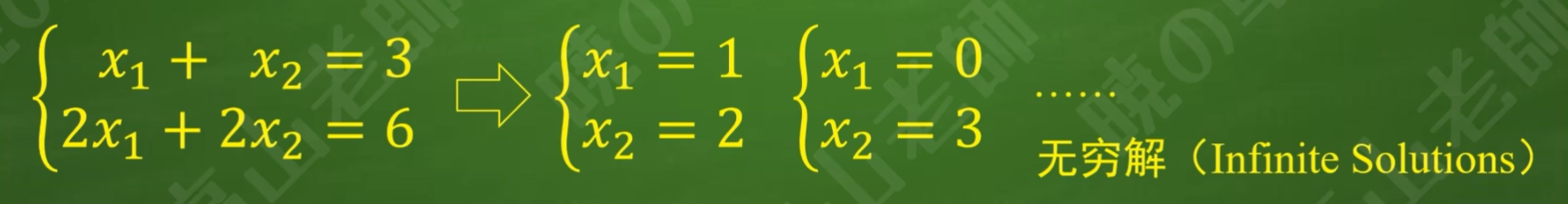
几何意义:
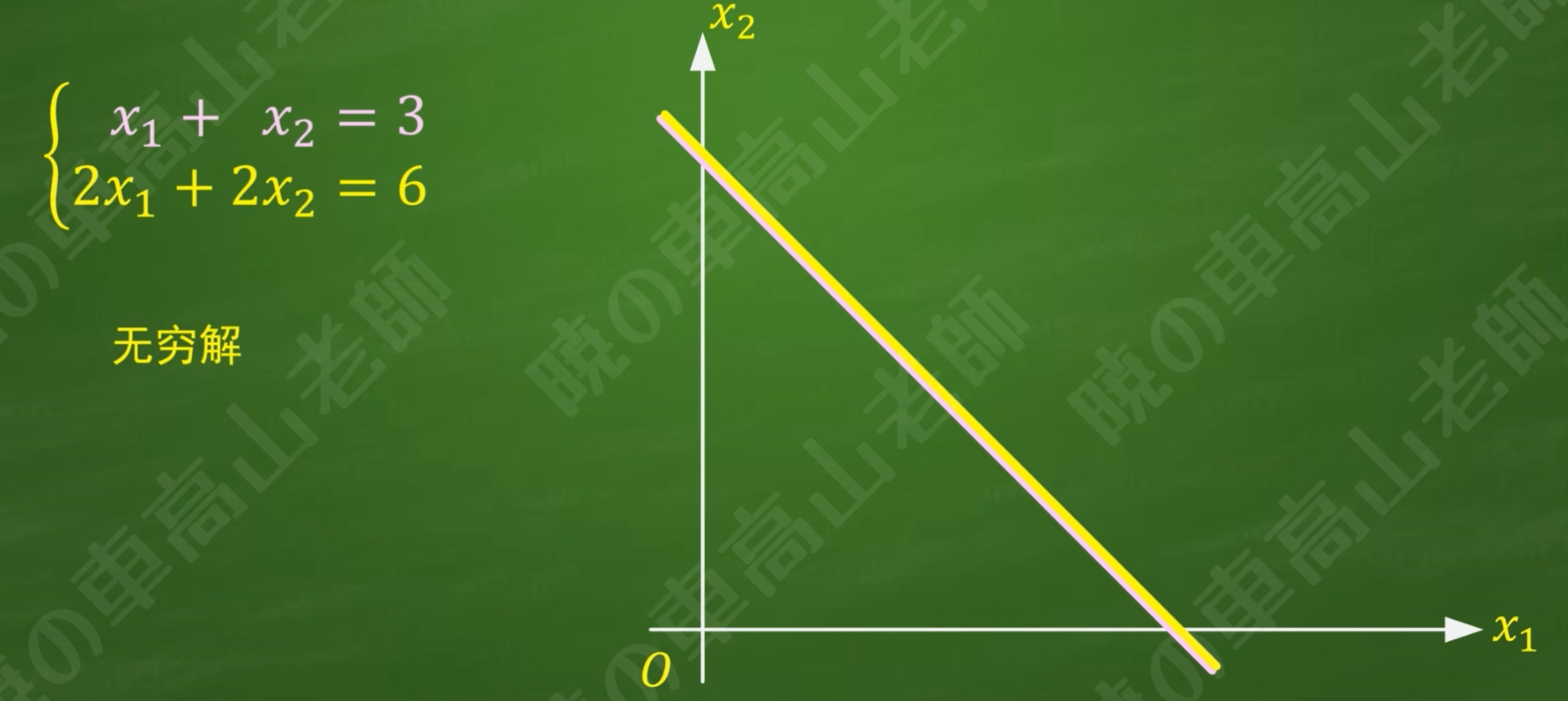
(3)无解

几何意义: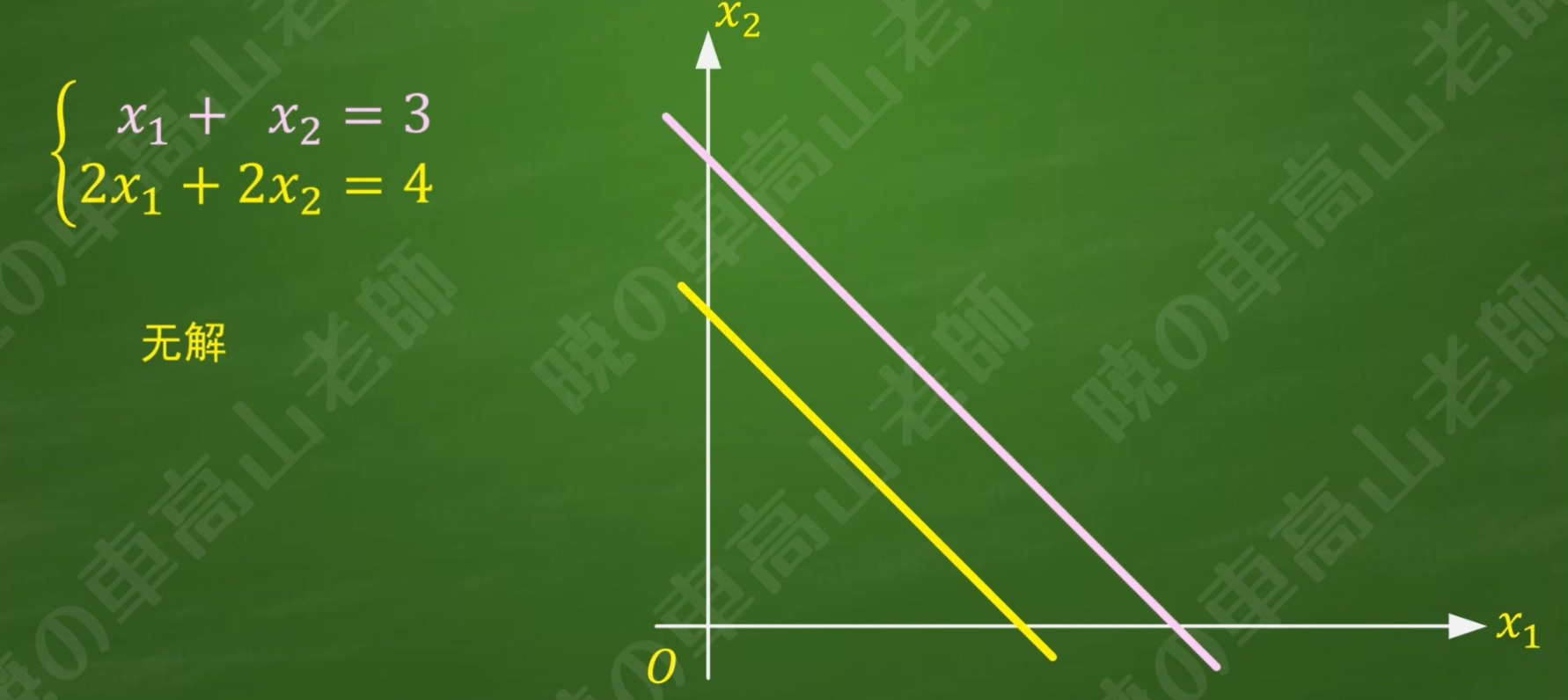
question:

3.系数矩阵和增广矩阵

增广矩阵需要有常数项并且常数项和系数矩阵的部分用虚线隔开
增广矩阵的初等行变换


4.非齐次线性方程组的解的判断
(1)唯一解

阶梯增广矩阵和阶梯系数矩阵的非0行数相等,且等于未知数个数,则非齐次线性方程组具有唯一解
(2)无穷解

阶梯增广矩阵和阶梯系数矩阵的非0行数相等,但小于未知数个数,则非齐次线性方程组具有无穷解
具有无穷解的非齐次方程组的通解结构
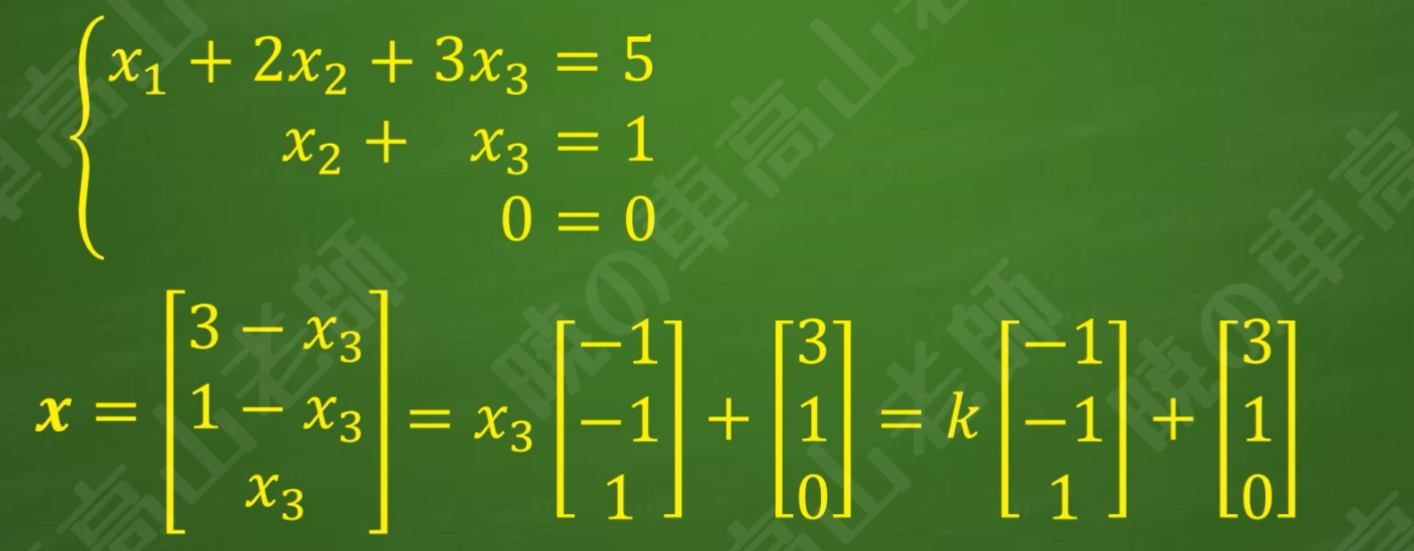
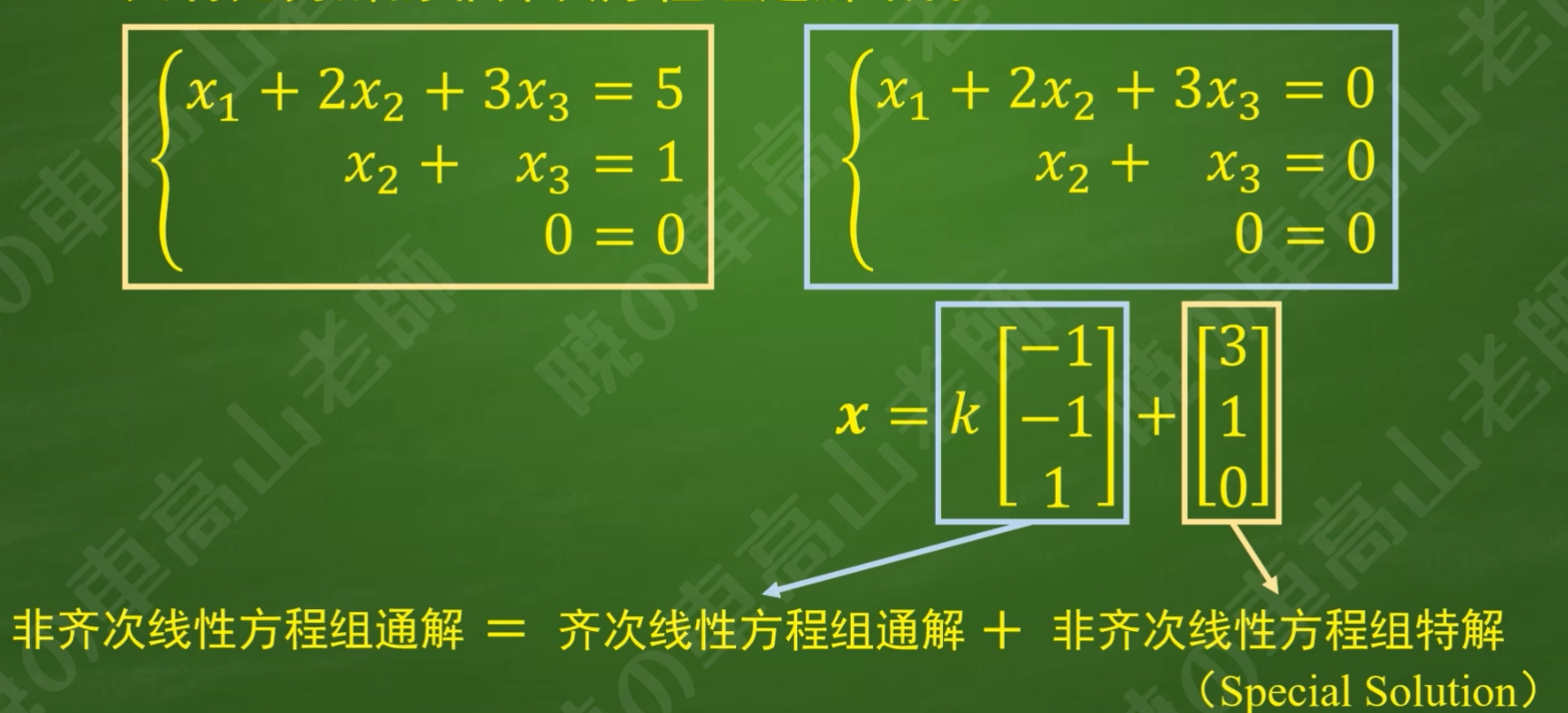
蓝色框框内的解为原非齐转化为齐次方程组的解,即为齐次通解
红色框框为原方程组无穷解中的一个特解
非齐通解=齐次通解+非齐特解
特解的求法

另所有自由变量为0
(3)无解


阶梯增广矩阵和阶梯系数矩阵的非0行数不相等,则非齐次线性方程组无解
5.例子——总结非齐次线性方程组解的判断和通解的求法
步骤1:根据非齐次线性方程组写出增广矩阵A|b,明确未知数个数n
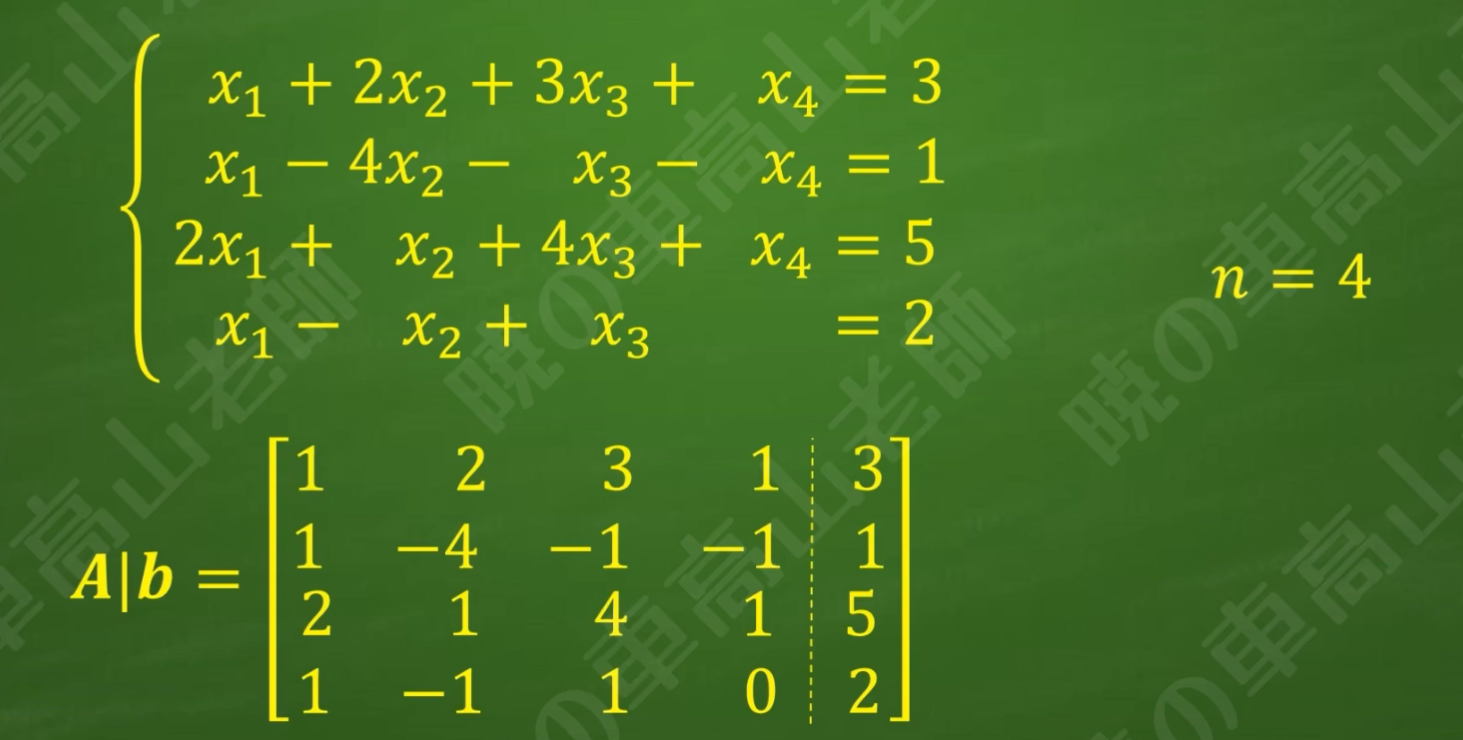
步骤2:对增广矩阵进行初等变换,最终变为阶梯矩阵
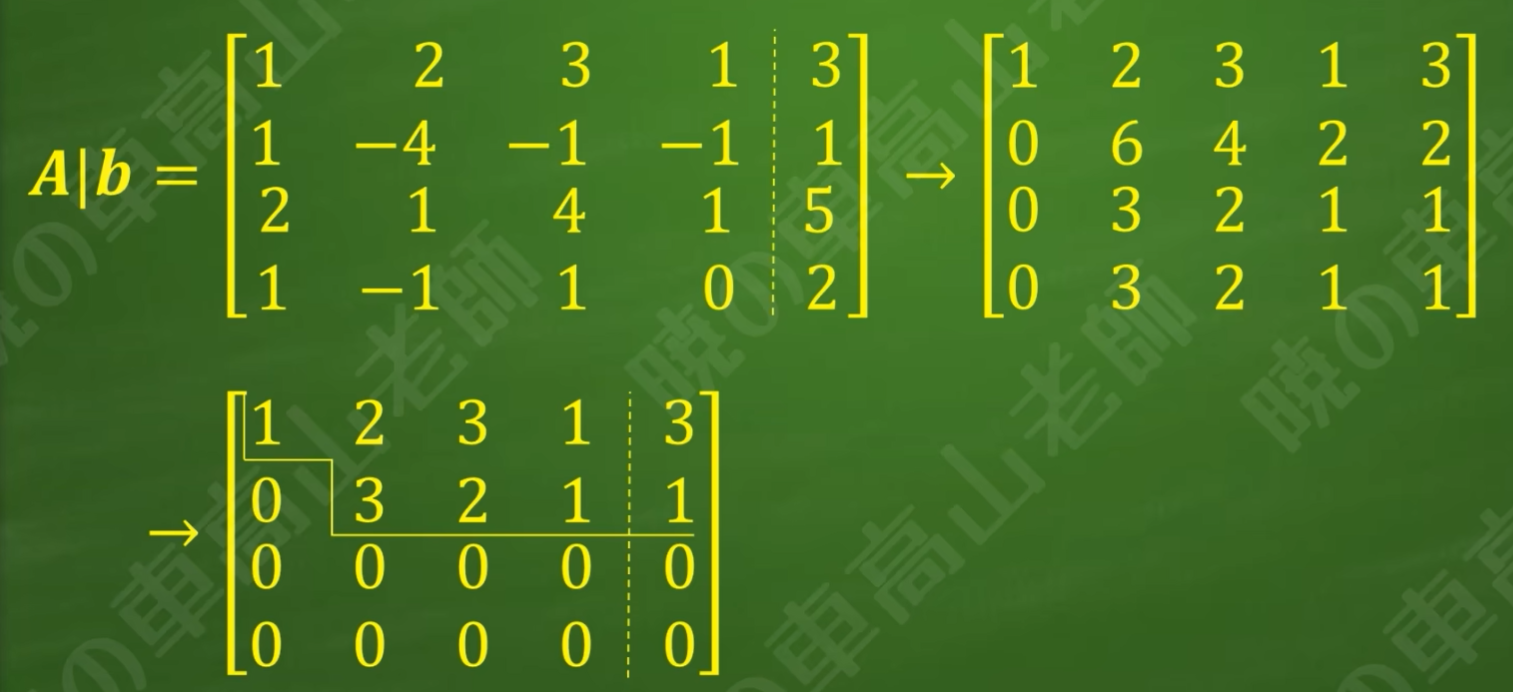
步骤3:查看对应的增广矩阵和系数矩阵的非0行数r(A|b)和r(A)
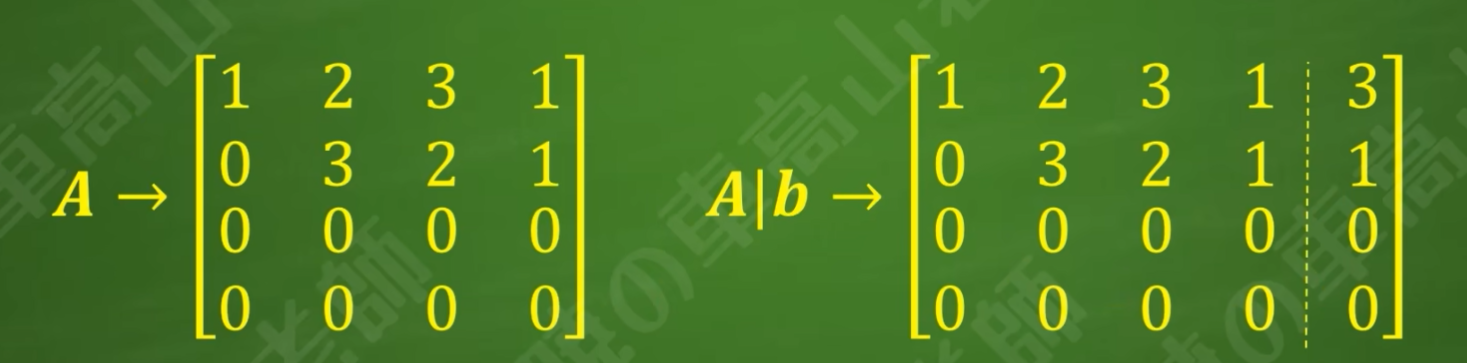
步骤4:判断方程组解的情况

根据准则进行判断
步骤5:对于具有无穷解的非齐次线性方程组,先找到主变量和自由变量,求出对应齐次线性方程组的基础解系,然后求出对应的通解x'
齐次通解:
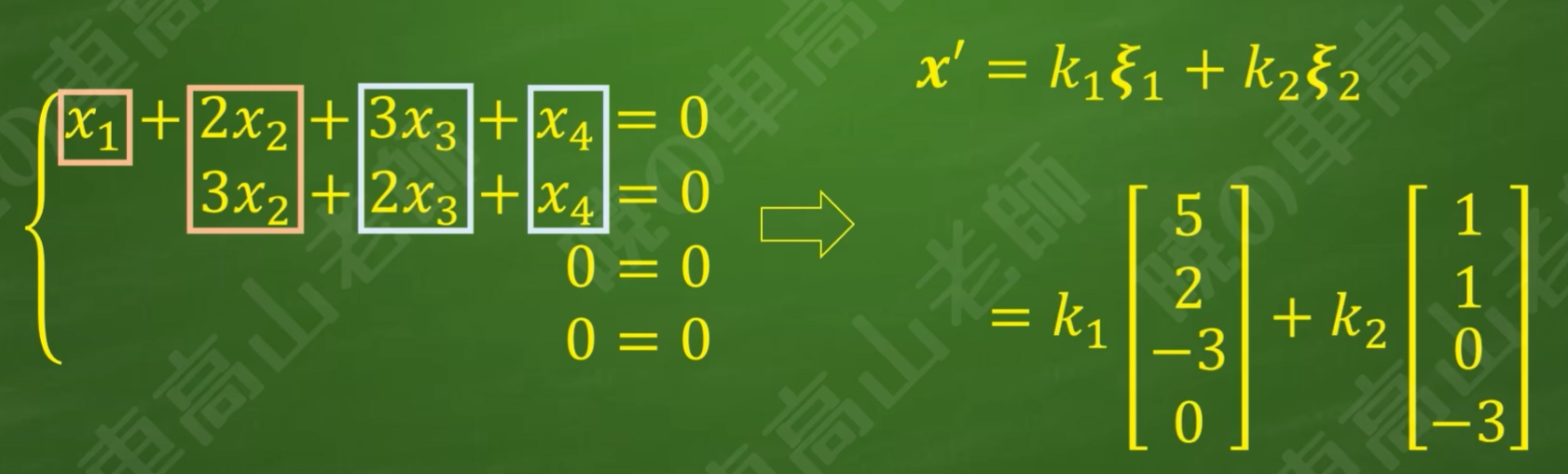
步骤6:在非齐次线性方程组里令全体自由变量为0,自底向上求出非齐次线性方程组的一个特解

步骤7:将齐次线性方程组的通解和非齐次方程组的特解相加就是非齐次线性方程组的通解
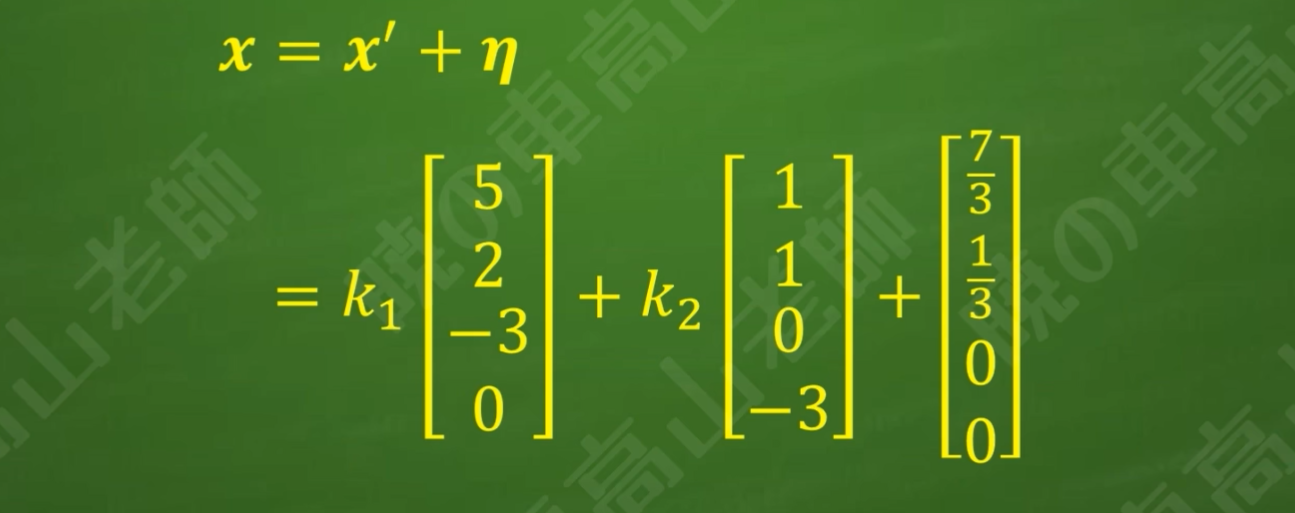
非齐次方程组的求解是以齐次方程组求解为基础,需要多加练习以熟悉掌握





















 3253
3253

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








