线性代数——俗说矩阵

文章内容主要来自：俗说矩阵：B站最宝藏的线性代数视频系列！一学就懂！_哔哩哔哩_bilibili

目录

一、初等矩阵

1.概念

2.矩阵的三种初等行变换

3.初等矩阵和初等行变换的关系

(1)置换阵*矩阵

(2)数乘阵*矩阵

(3)倍加阵*矩阵

二、逆矩阵的概念

1.前情回顾

2.引例

3.什么样的矩阵存在逆矩阵？

4.一个矩阵的逆矩阵唯一吗？

5.总结

---

一、初等矩阵

1.概念

对单位阵E进行1次初等变换得到的矩阵叫做初等矩阵（Elementary Matrix）

2.矩阵的三种初等行变换

(1)置换：交换两行的位置

(2)数乘：给某一行乘以非零常数k

(3)倍加：将某一行的k倍加到另一行上

3.初等矩阵和初等行变换的关系

   对矩阵实施一次初等行变换相当于给这个矩阵左乘一个初等矩阵

(1)置换阵*矩阵

给矩阵左乘置换阵，相当于对矩阵进行了一次相应的置换初等行变换

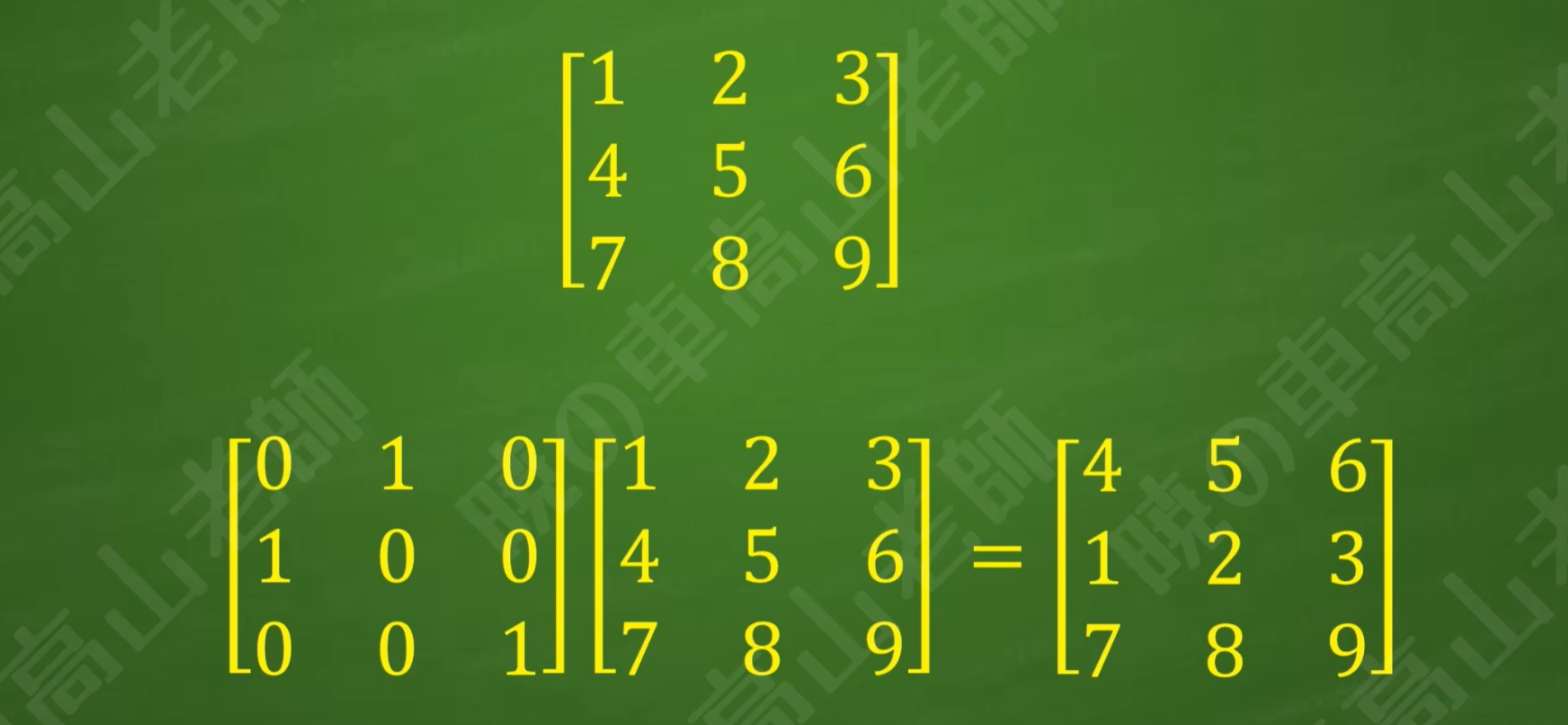
（左乘换行，右乘换列）

(2)数乘阵*矩阵

给矩阵左乘数乘阵，相当于对矩阵进行了一次相应的数乘初等行变换

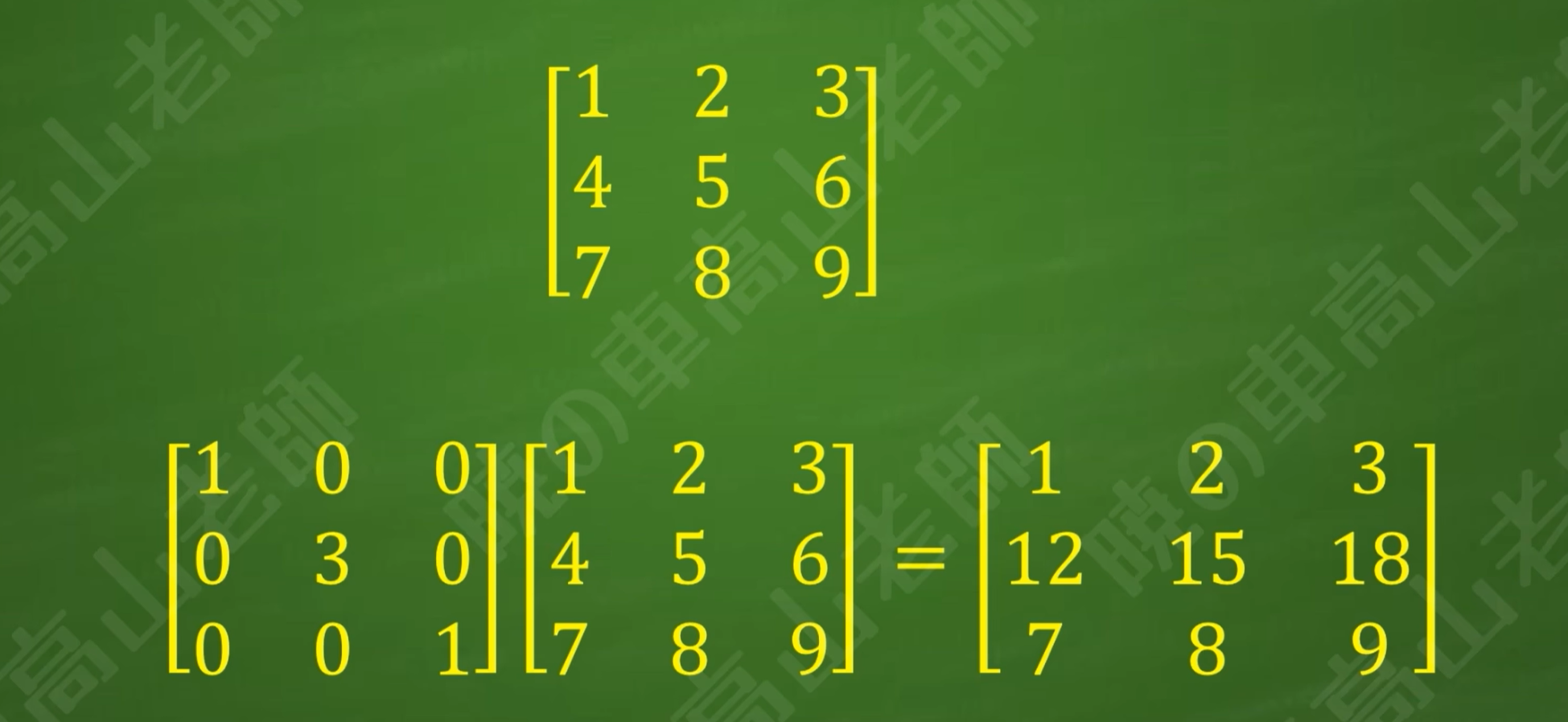
(3)倍加阵*矩阵

给矩阵左乘倍加阵，相当于对矩阵进行了一次相应的倍加初等变换

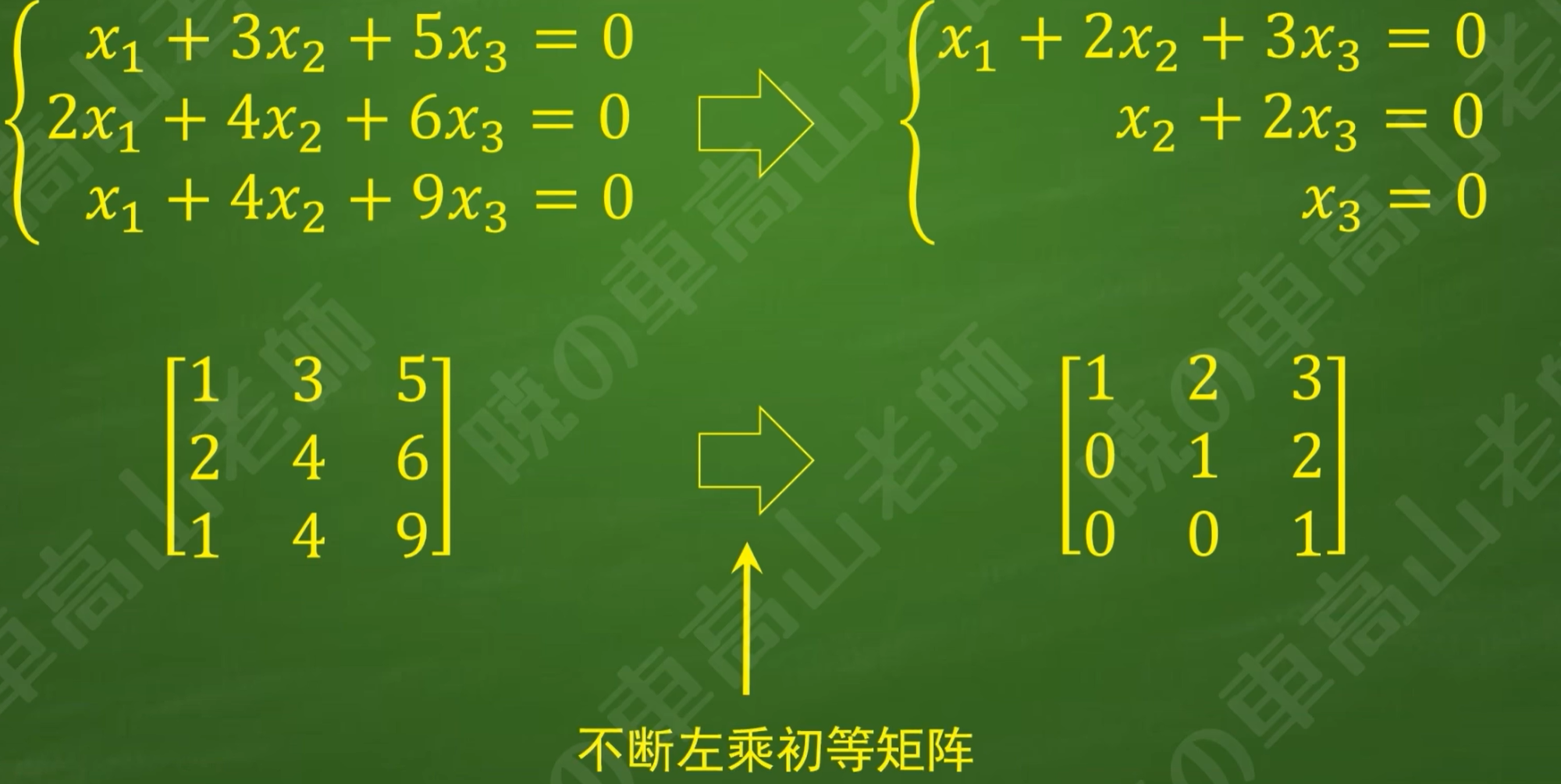
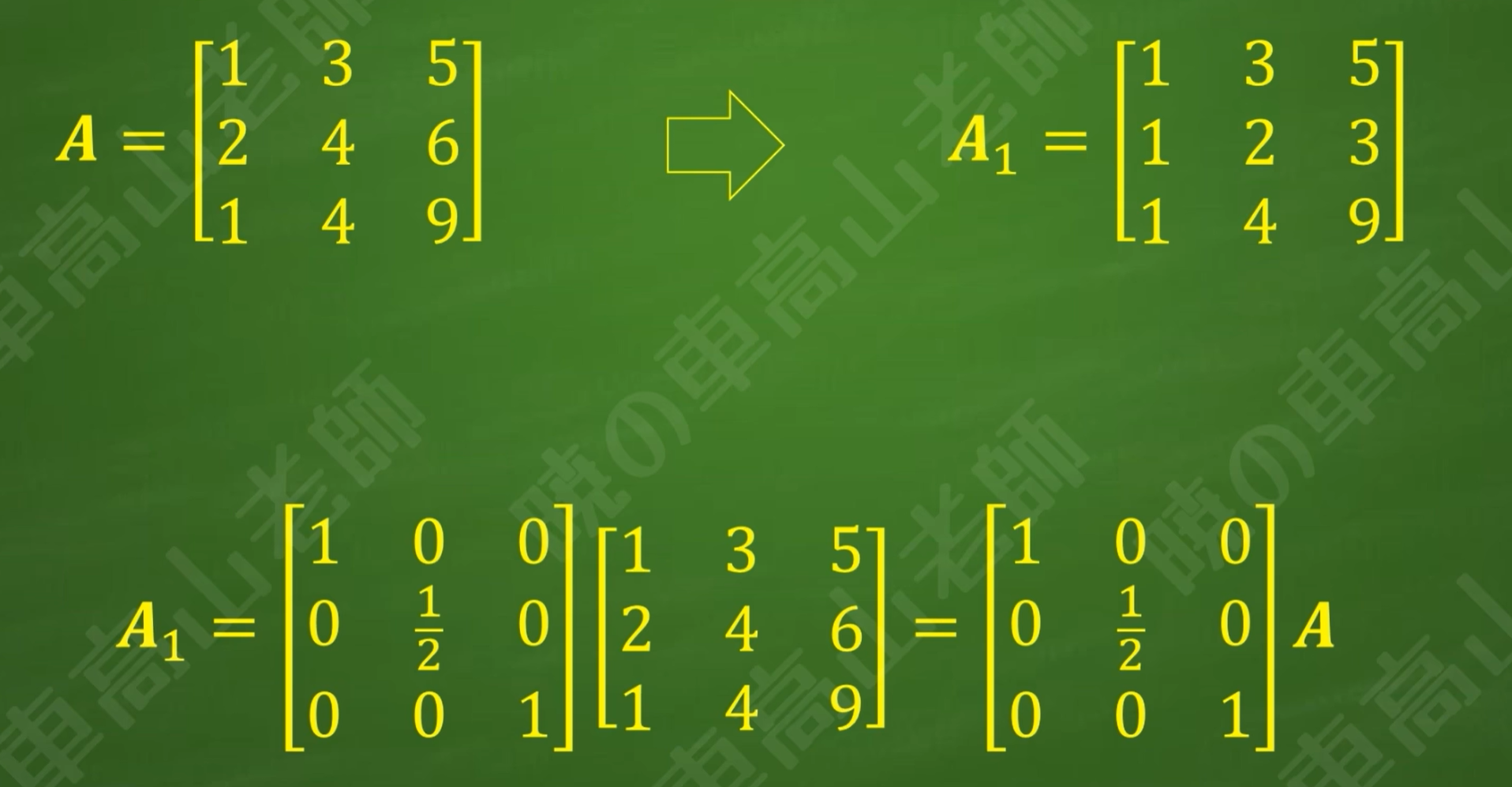
矩阵乘法具有结合律

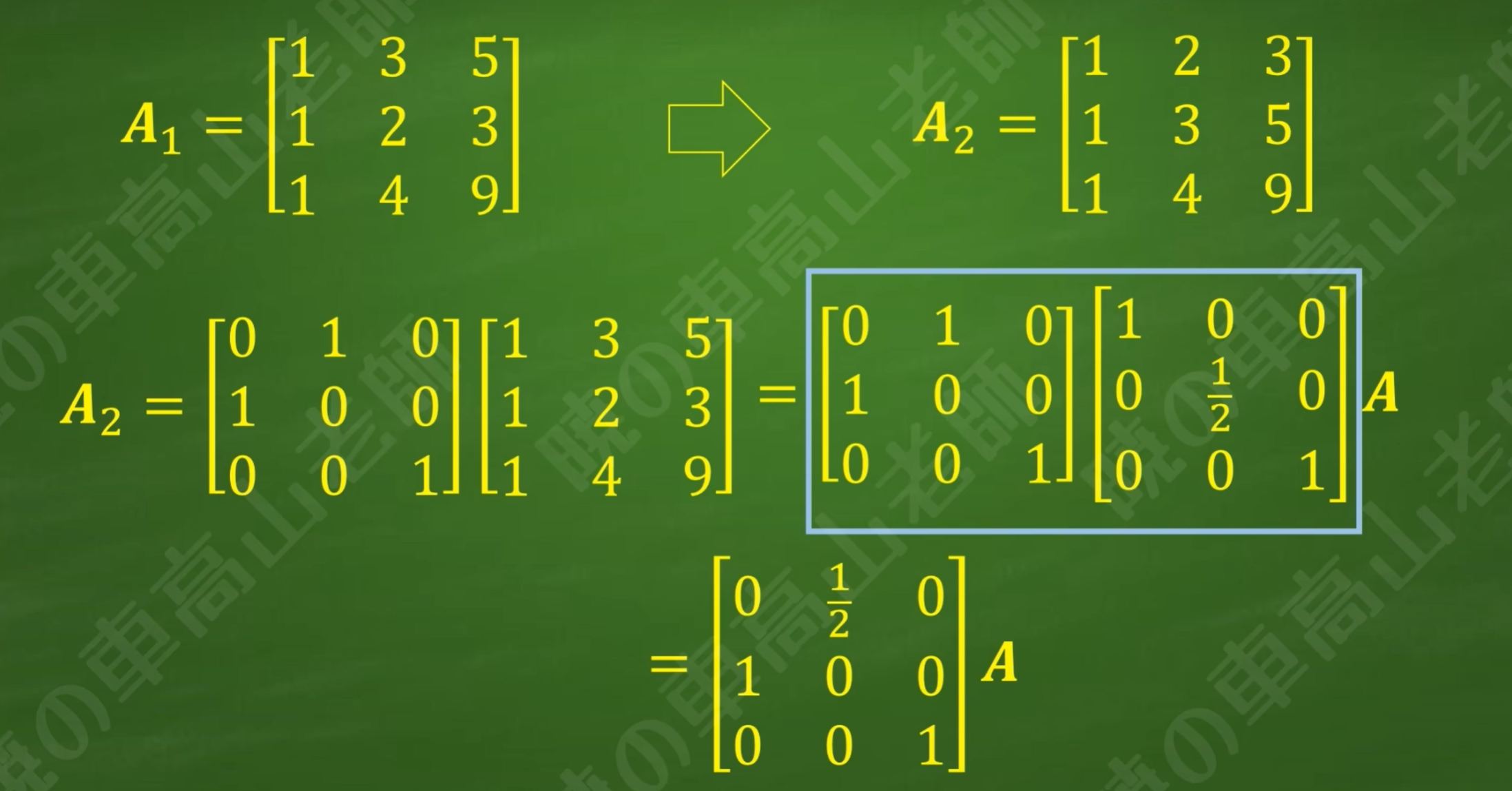
矩阵经几次变换成为另一个矩阵，相当于给该矩阵左乘一个行变换矩阵

行变换矩阵是由若干个初等矩阵依次相乘而得，初等矩阵的内容和顺序对应初等行变换的倒序（也就是最开始的初等行变换的初矩阵最靠近A，最后的初等行变换的初等矩阵最远离A）

二、逆矩阵的概念

1.前情回顾

对矩阵A每次进行一次初等行变换，就给它左乘一个对应的初等矩阵，这些初等矩阵的乘积就是从A到初等变换t次后的矩阵At的映射矩阵Kt

2.引例

我们也能实现让右上角的元素为0

A的逆矩阵计算如下:

由此我们得到A的逆矩阵：

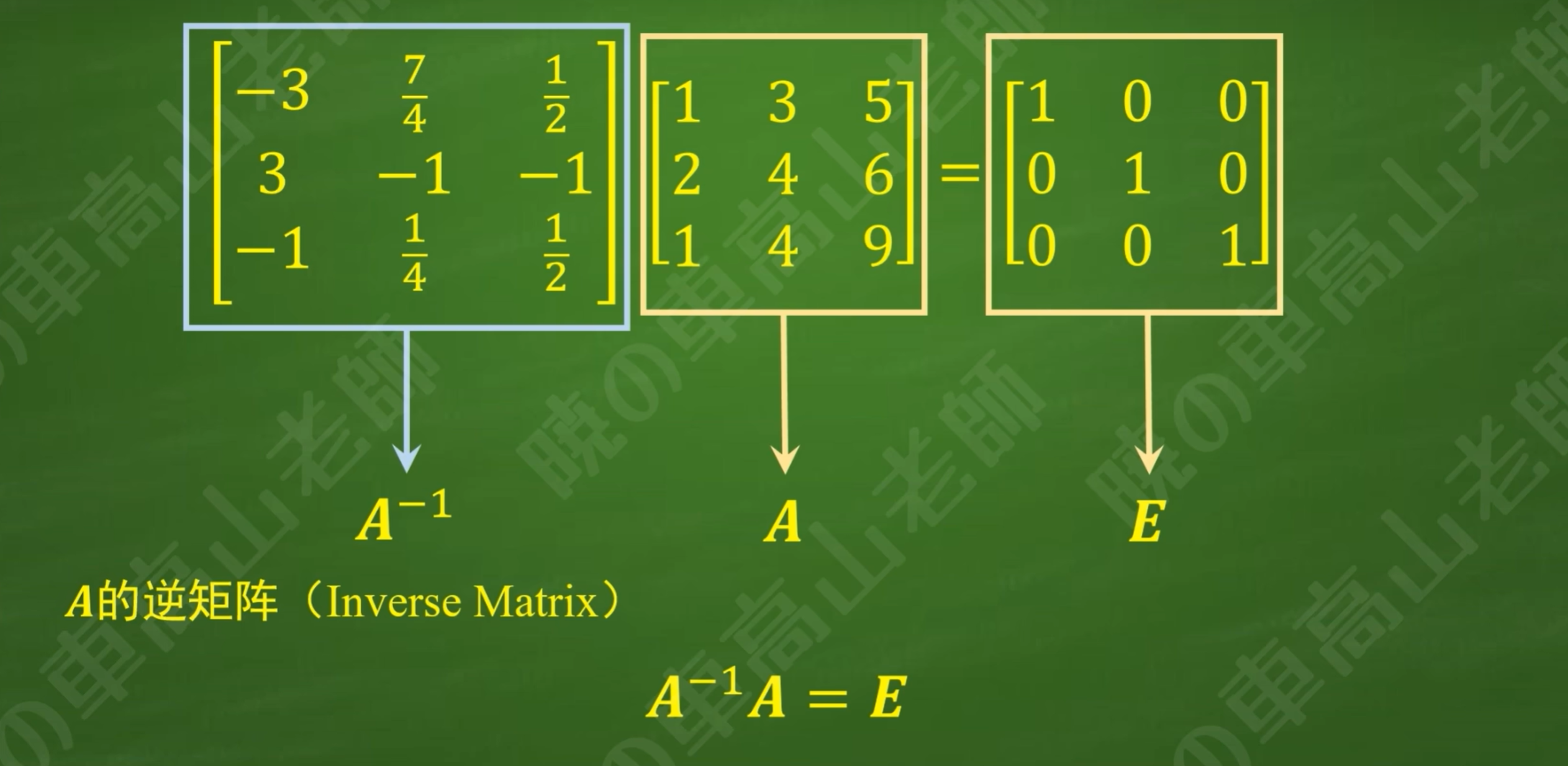
   对A的逆矩阵再求逆矩阵是A本身

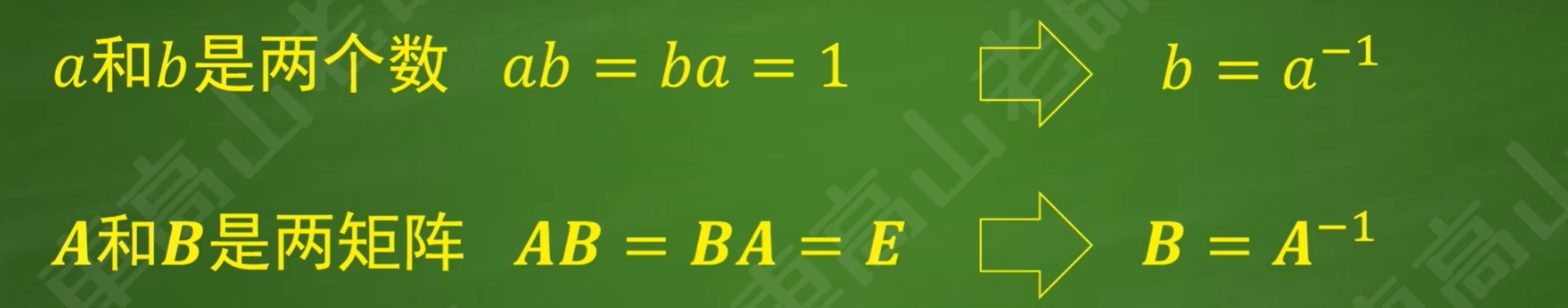
什么样的矩阵存在逆矩阵？

一个矩阵的逆矩阵唯一吗？

怎么样计算一个矩阵的逆矩阵？

接下来主要针对第一、二个问题回答

3.什么样的矩阵存在逆矩阵？

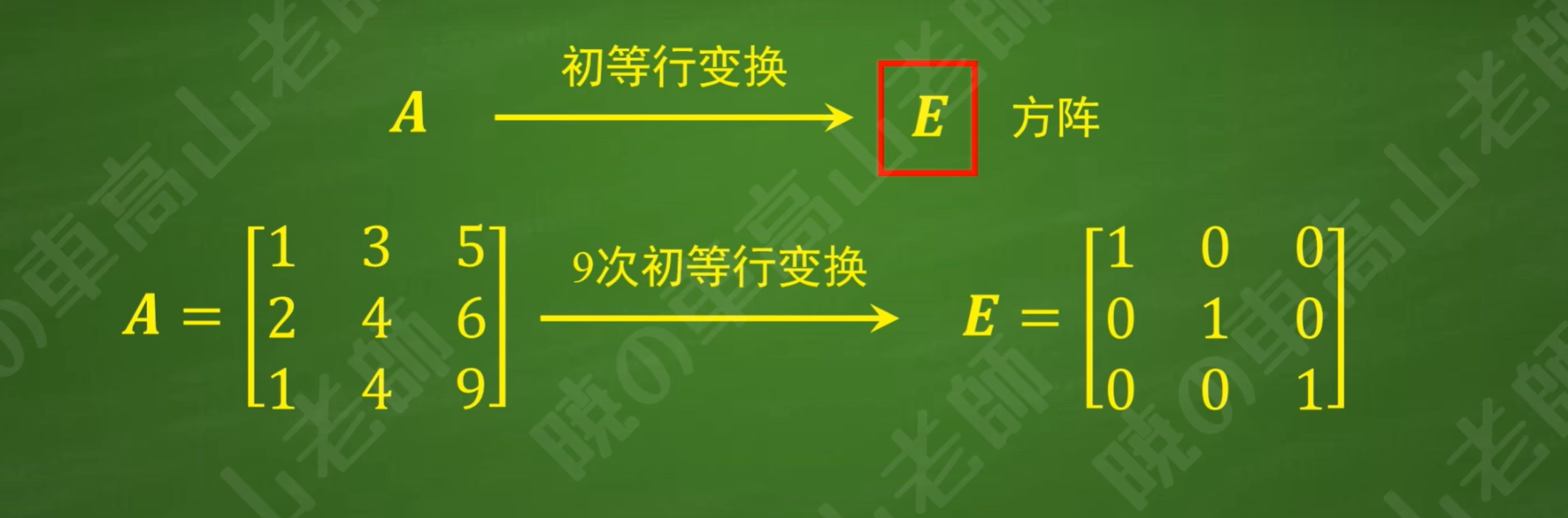初等行变换不改变矩阵的大小（尺寸），因此只有方阵才可以求逆矩阵

矩阵可逆的第一个条件：矩阵必须是行列数相等的方阵

设A是n*n的矩阵，则E也是n*n的矩阵

一个方阵的逆矩阵也必为同等大小的方阵

A与A的逆矩阵和E都是n*n矩阵  r(E)=n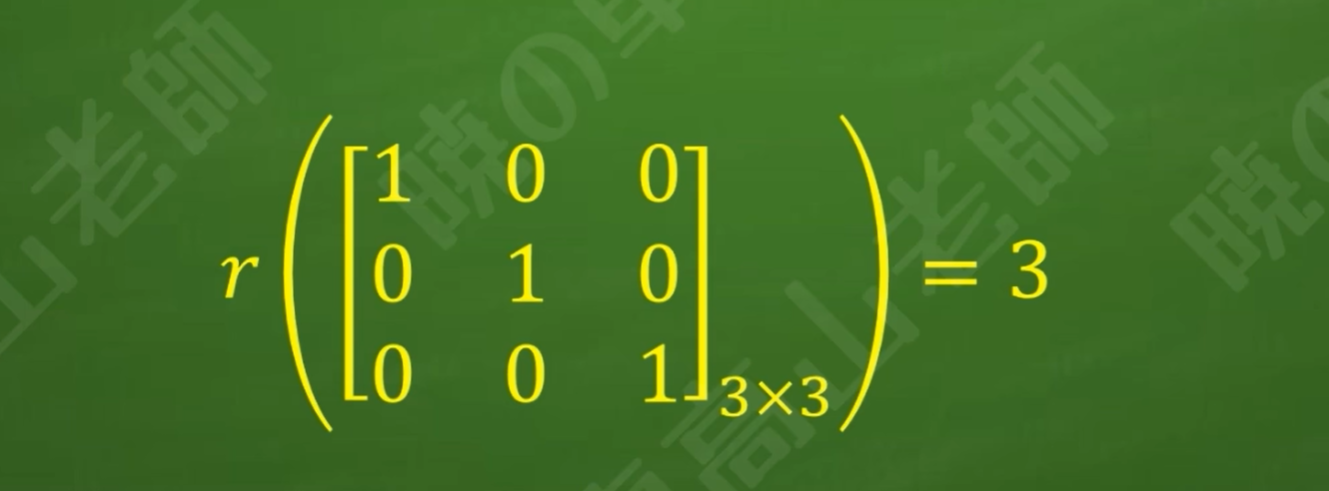

初等行变换不改变矩阵的秩，因此有：r(A)=r(E)=n

如果一个方阵可逆，则它的秩必和其行列数相等

一个方阵的逆矩阵的秩也必和其行列数相等

(1)可逆的矩阵能通过初等行变换转化为单位阵

(2)不可逆的矩阵不能通过初等行变换转化为单位阵

可逆矩阵及其逆矩阵都可以表示为若干个初等矩阵相乘的结果

推论：初等矩阵一定可逆，若干个初等矩阵的乘积也一定可逆

4.一个矩阵的逆矩阵唯一吗？

设有两个矩阵B和C，使得两者都是A的逆矩阵，根据矩阵定义：

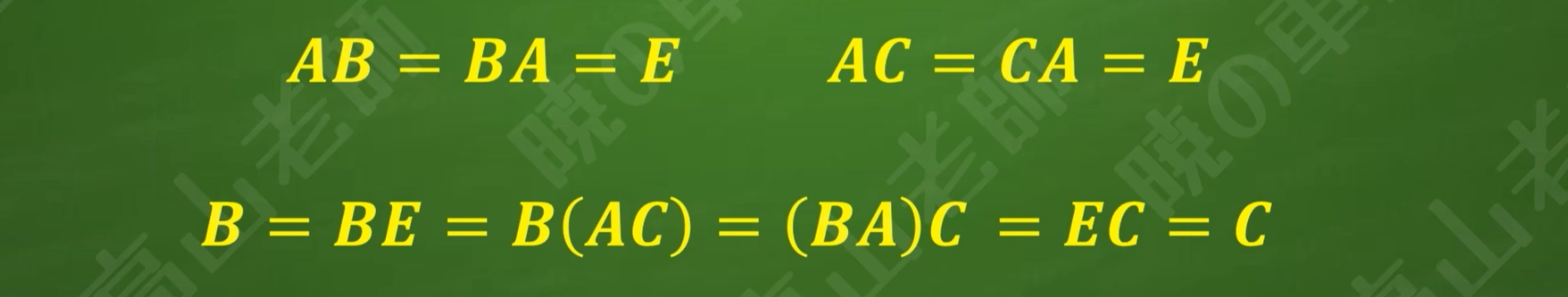
一个矩阵如果可逆，则其逆矩阵是唯一的

5.总结

(1)矩阵存在逆矩阵的前提是行列数相等（方阵），且秩等于行列数

(2)一个矩阵和其逆矩阵可交换，乘积为单位阵

(3)可逆的矩阵可以通过若干次初等行变换转化为单位阵

(4)可逆的矩阵及其逆矩阵可以表示为若干初等矩阵的乘积

(5)逆矩阵是唯一的