线性代数自学——俗说矩阵

视频内容来自：俗说矩阵：B站最宝藏的线性代数视频系列！一学就懂！_哔哩哔哩_bilibili

本篇主要来源：7-特殊矩阵乘法_哔哩哔哩_bilibili

目录

一、特殊矩阵乘法

1.零矩阵

2.对角阵

3.单位阵

4.规律：两个矩阵乘积的秩，不超过每一个乘数矩阵的秩

二、矩阵乘法的性质

1.复习上一章内容

2.矩阵乘法的结合律

3.矩阵的转置：行列换位

4.方阵

可交换矩阵

矩阵乘方

对角阵乘方

纯量阵

---

一、特殊矩阵乘法

1.零矩阵

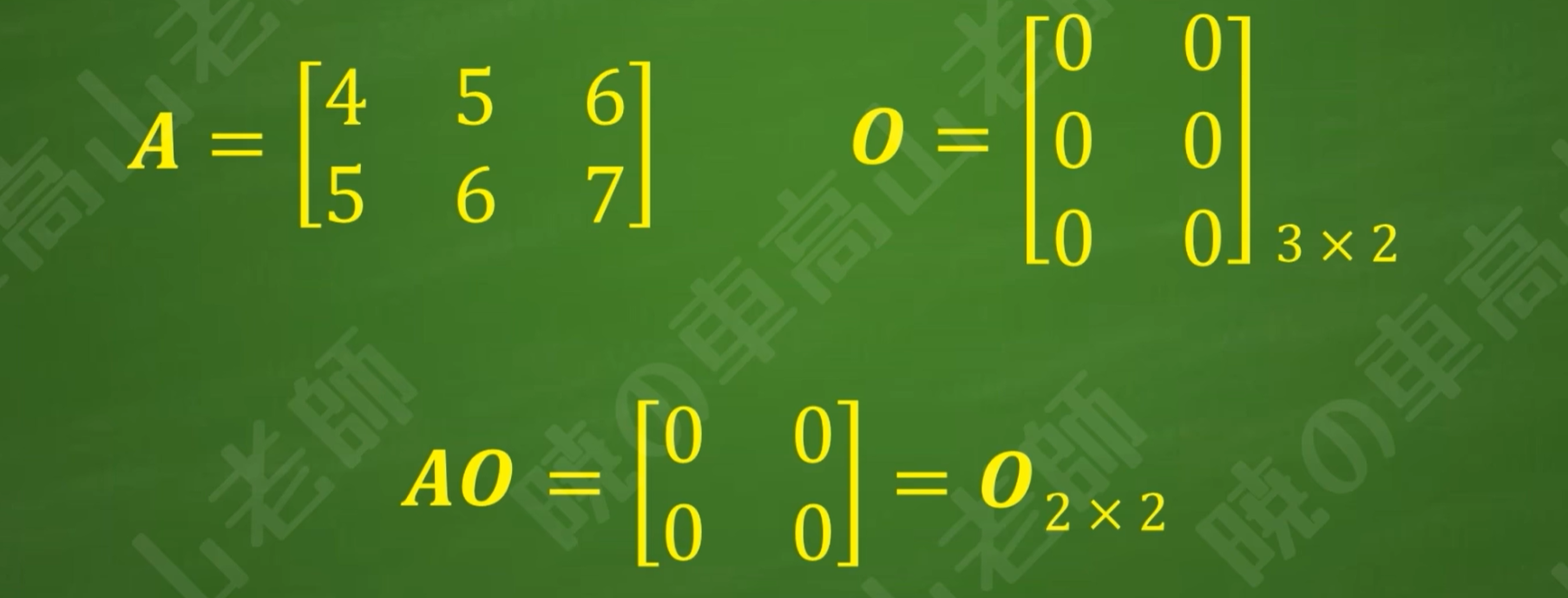
在矩阵乘法可行的条件下，A和零矩阵O相乘的结果是零矩阵

注意：虽然结果零矩阵和乘数零矩阵都是O，但是大小不一样

当两个乘数矩阵有一个是零矩阵，结果一定是零矩阵

反之，如果两个矩阵相乘结果是零矩阵，是否说明两个矩阵其中一个是零矩阵呢？

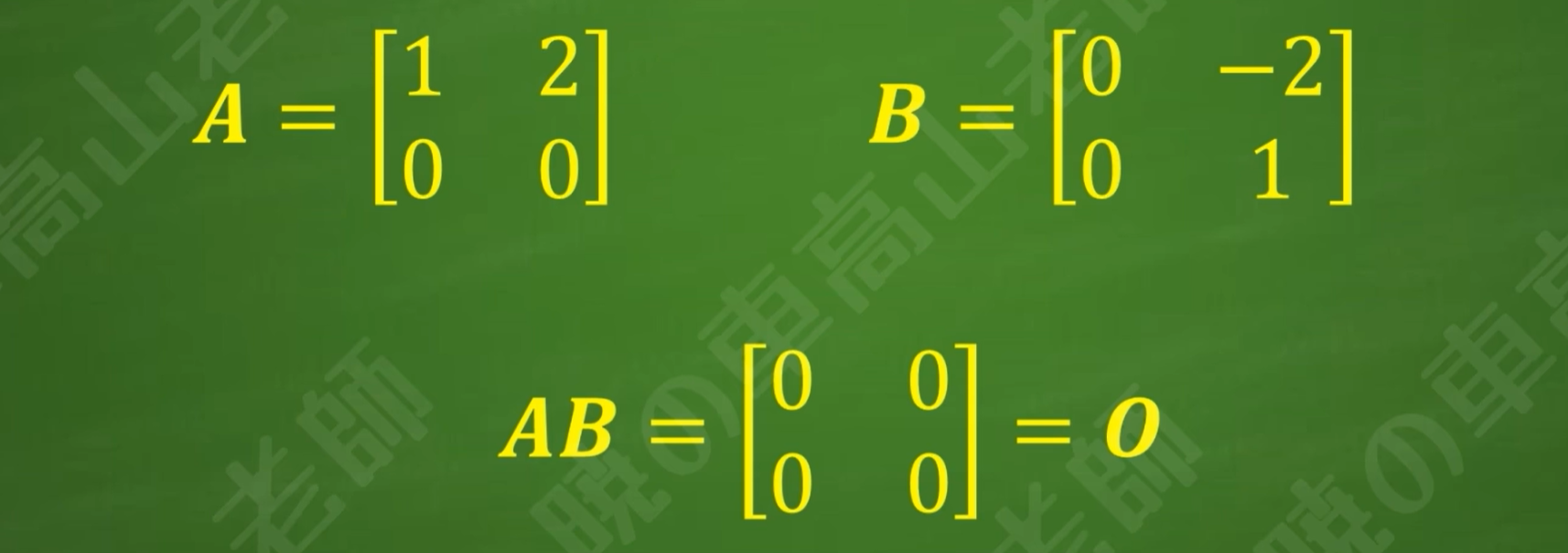
(1)AB=O，并不意味着A=O或B=O

(2)若A=O或B=O，则必有AB=O

(3)若AB≠O，则必有A≠O且B≠O

和线性方程组联系

(1)AB=O，并不意味着A=O或B=O    =>   齐次线性方程组Ax=0中，可能存在x≠0的非零解

(3)若AB≠O，则必有A≠O且B≠O    =>   非齐次线性方程组Ax=b若有解，必有x≠0，即非齐次线性方程组必不存在零解

2.对角阵

对于一个行列数相等的矩阵，如果行列标号不等位置对应的元素都是0，则称这个矩阵是对角阵（Diagonal Matrix）

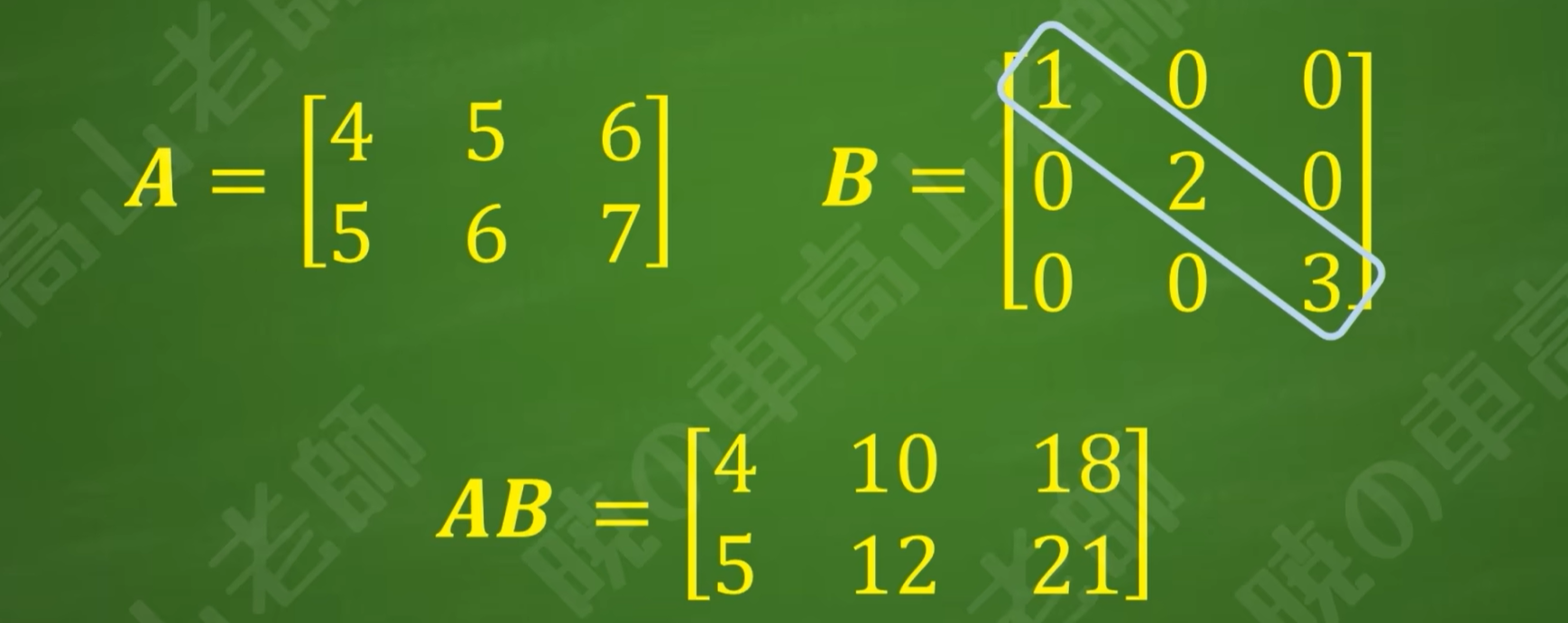
行列标号相等位置对应的元素构成了主对角线(Main DIagonal)

3.单位阵

主对角线元素全为1的对角矩阵称为单位阵(Identity Matrix)，记为E（有的文献中写作I）

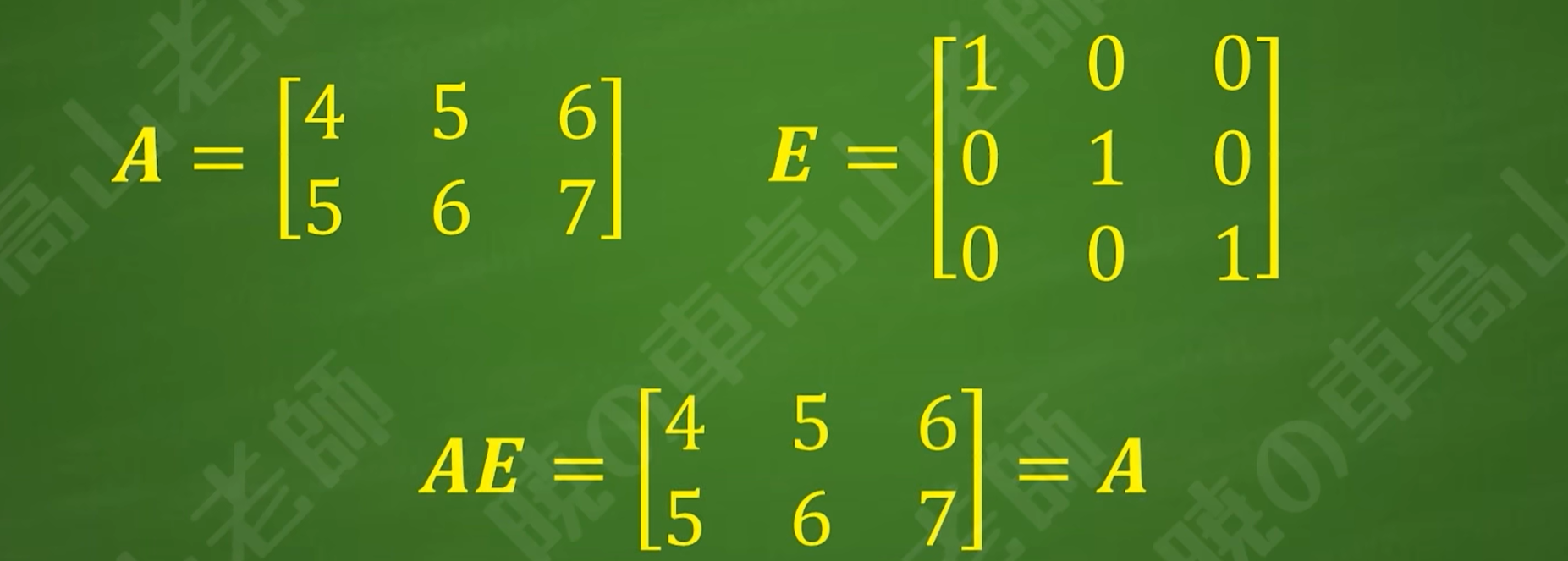
在矩阵乘法可行的条件下，A和单位阵E相乘的结果是A本身（A可以在左边或者右边，符合矩阵乘法的条件即可）

4.数量积

一个行向量乘以一个列向量，向量维数必须相等，结果为一个数字，相当于两个向量的数量积

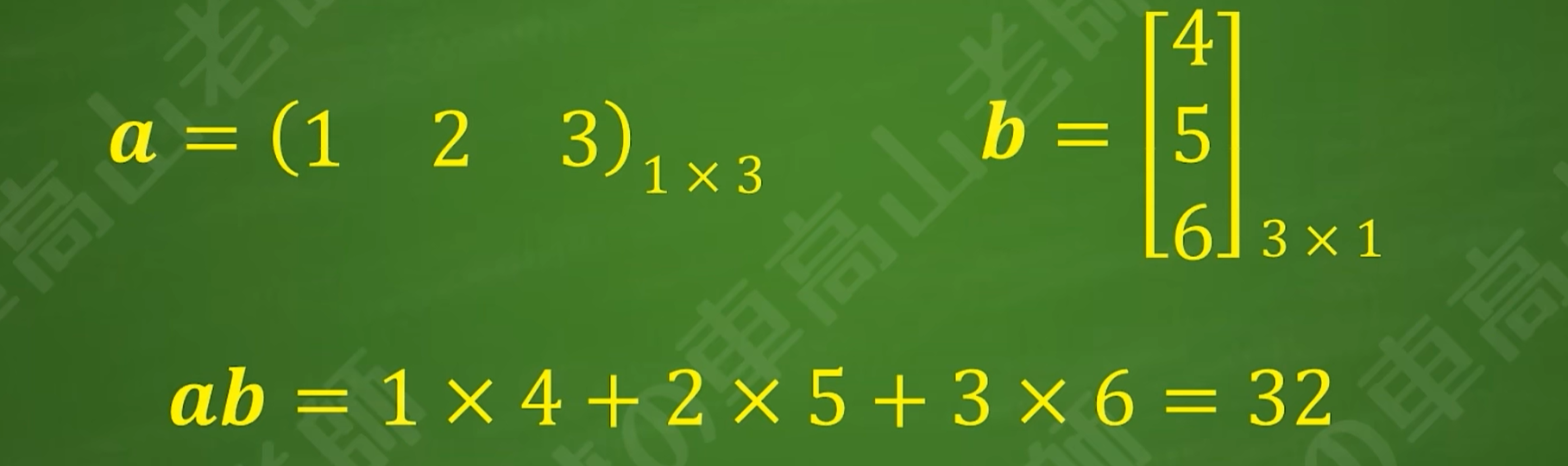
一个列向量乘以一个行向量，结果是一个各行各列成比例的矩阵

简便算法：直接将行向量代入列向量里整体运算，亦可将列向量代入行向量里整体运算

4.规律：两个矩阵乘积的秩，不超过每一个乘数矩阵的秩

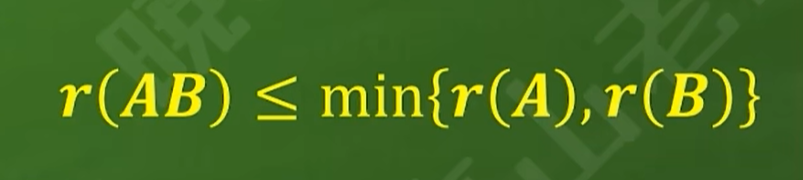
二、矩阵乘法的性质

1.复习上一章内容

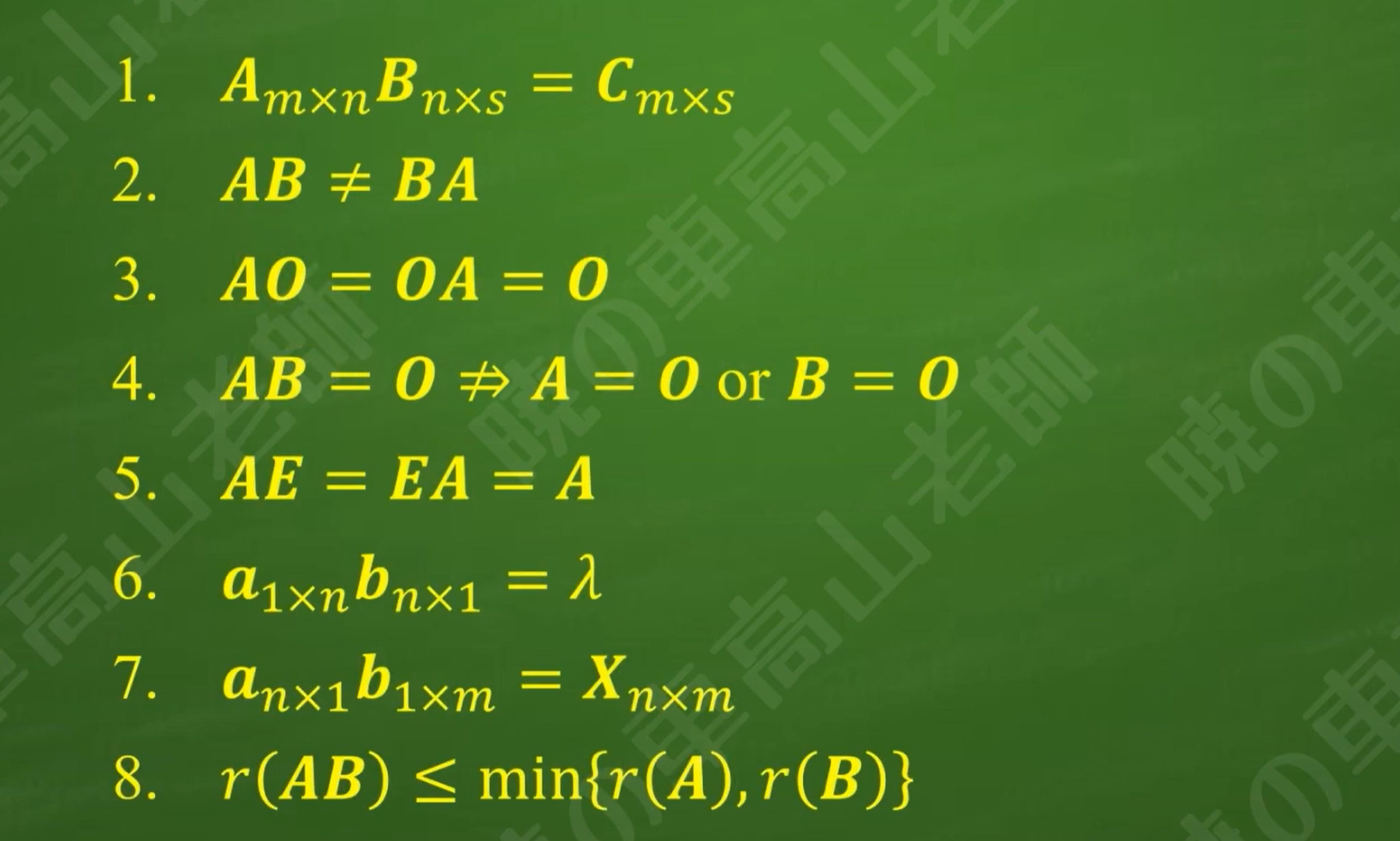
2.矩阵乘法的结合律

例子认证

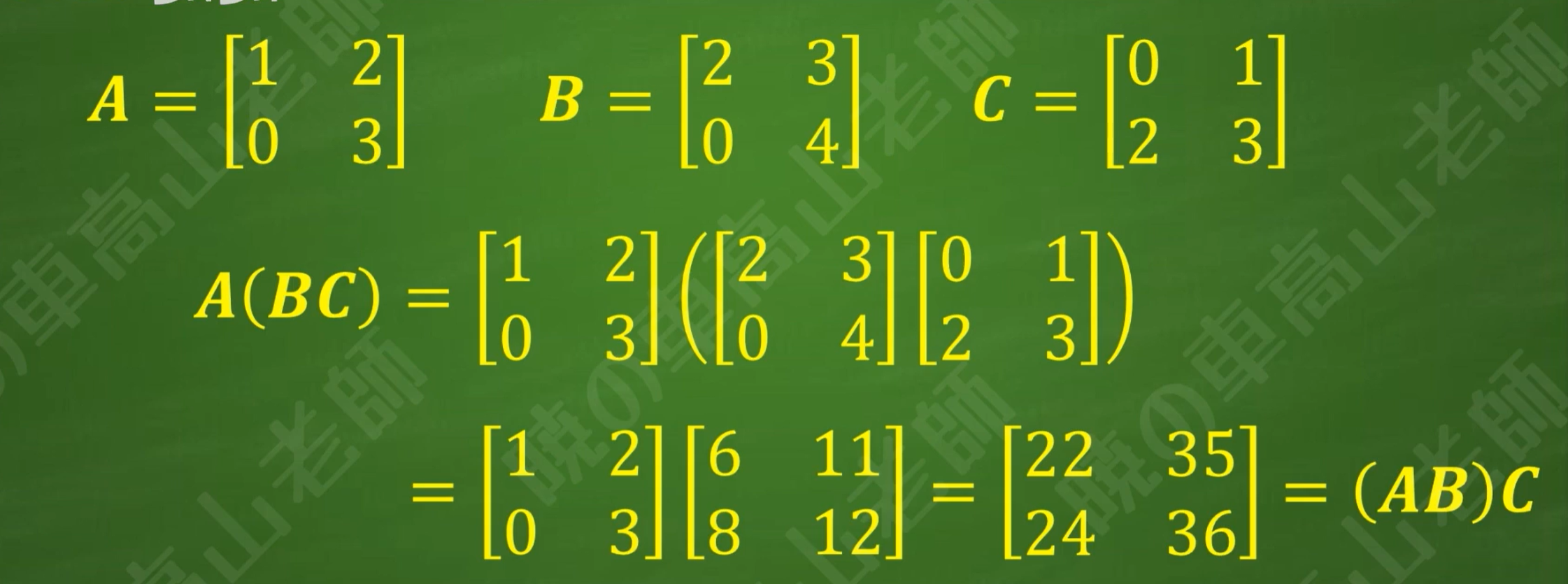
在满足矩阵乘法条件的前提下，矩阵乘法具有结合律

矩阵乘法具有结合律的本质原因是复合映射具有结合律

3.矩阵的转置：行列换位

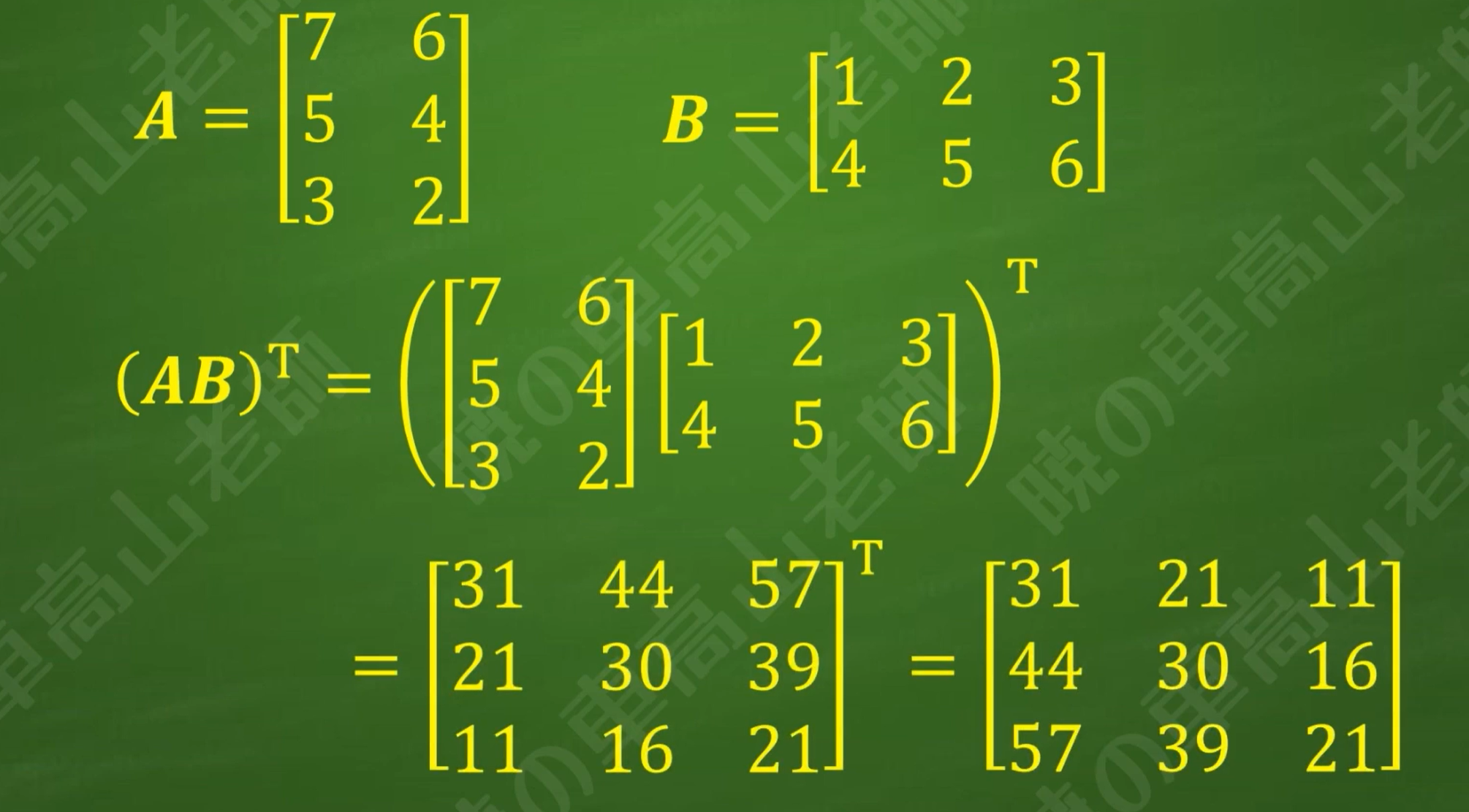
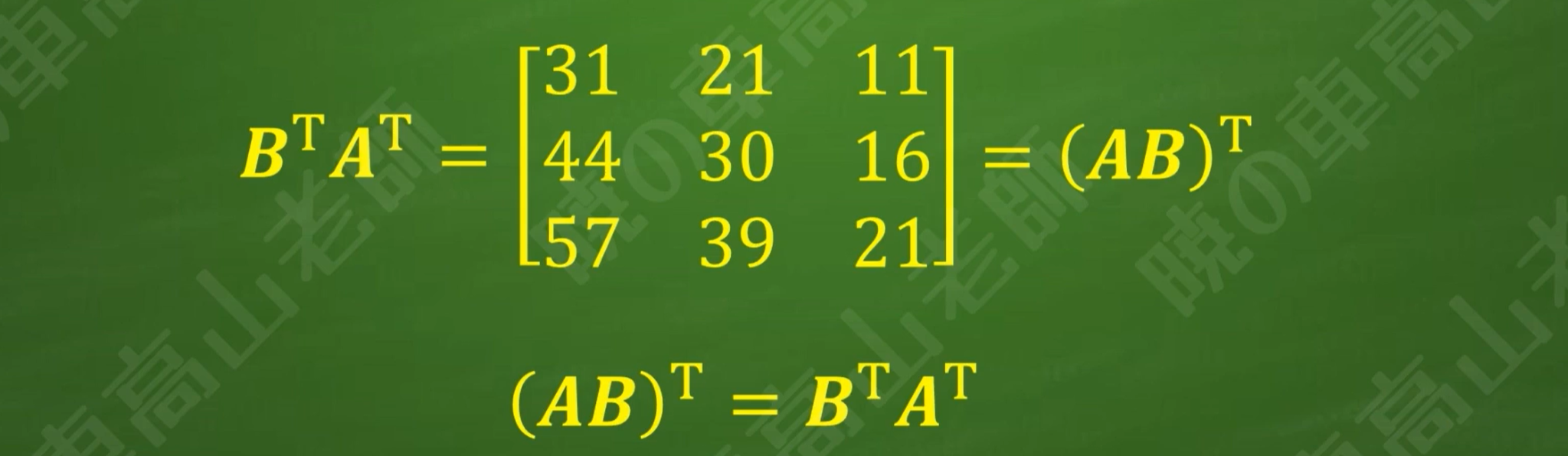
两个矩阵相乘后取转置，等于每个矩阵转置后反向相乘

4.方阵

行列数相同的矩阵称为方阵

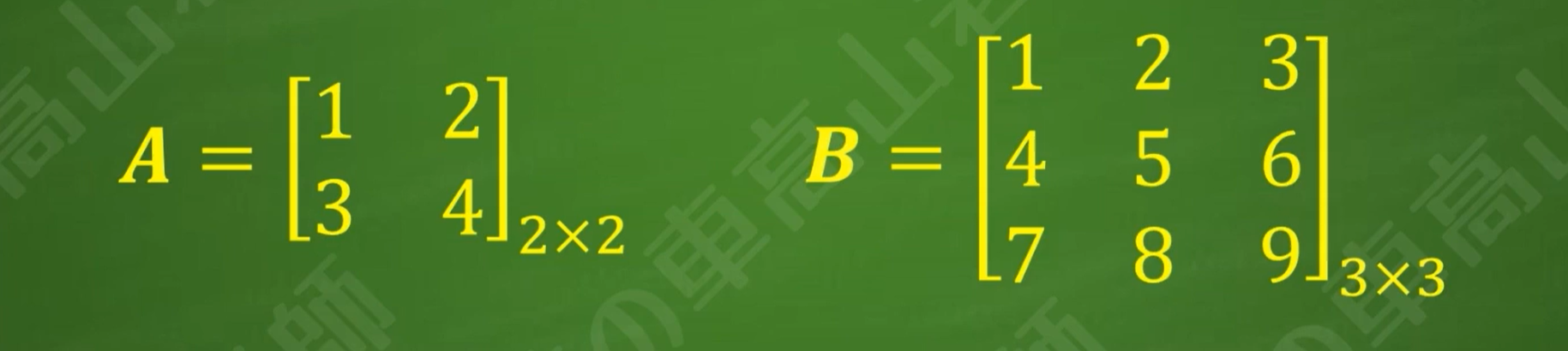
可交换矩阵

A*B不一定等于B*A，因为矩阵乘法没有交换律，但不代表任意一个矩阵乘法都没有交换律

矩阵乘方

可以乘方的矩阵必须是方阵，否则乘方不满足矩阵乘法的基本条件

且有以下补充规定：

与之前功能有何不同：

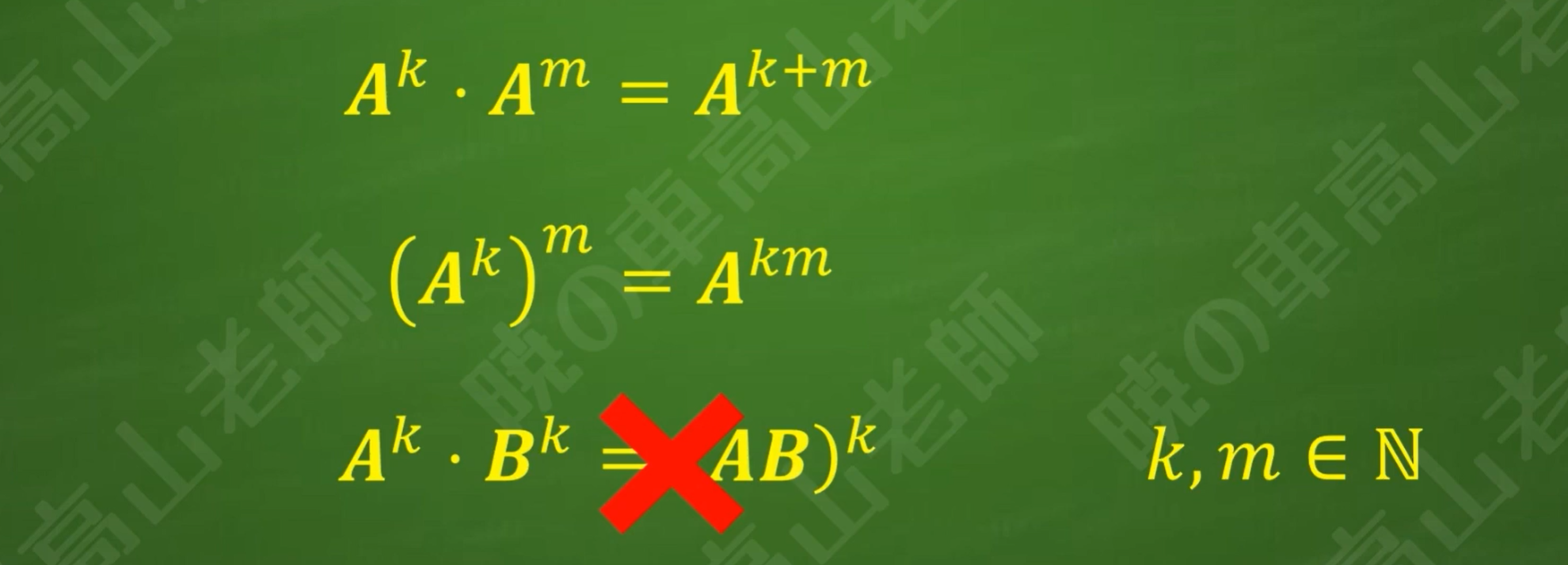
对角阵乘方

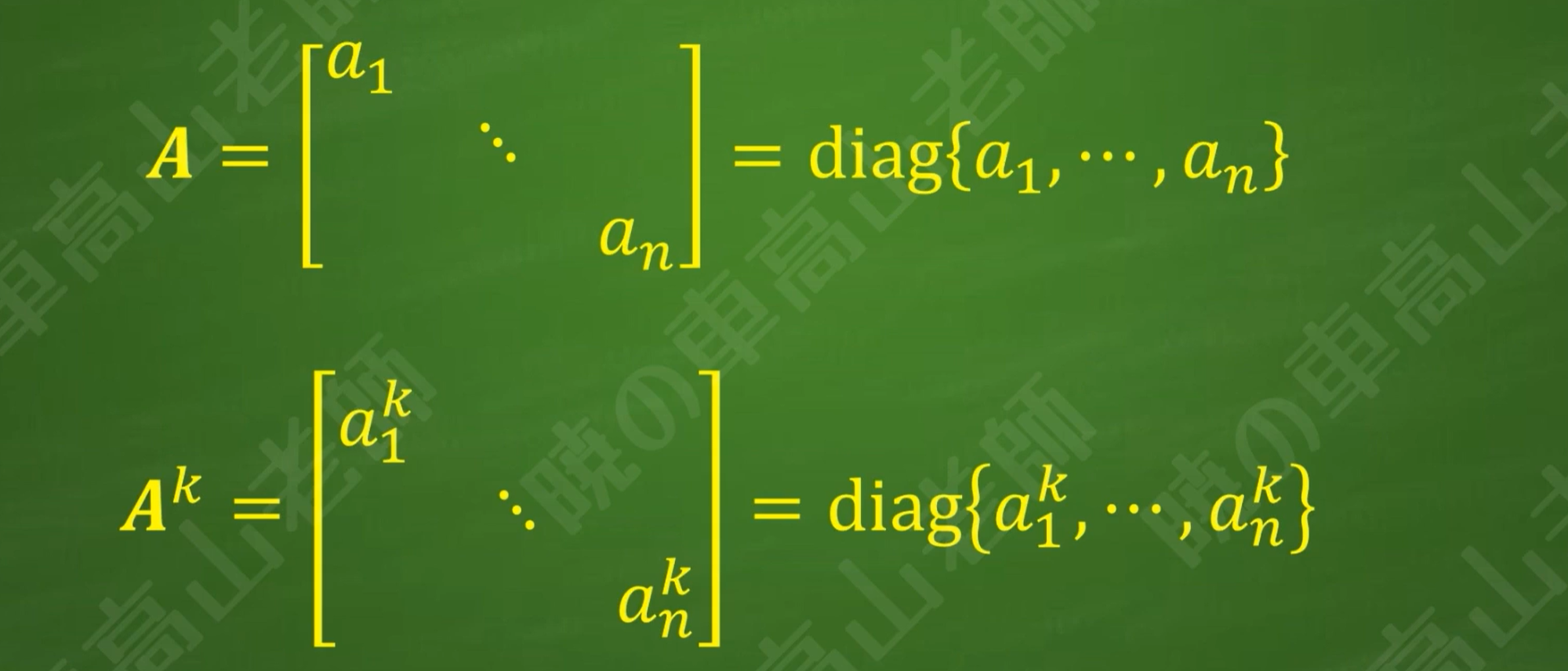
对角阵的乘方结果仍然是对角阵，只需要给各个对角线元素进行乘方运算即可

纯量阵

主对角线元素全部相等

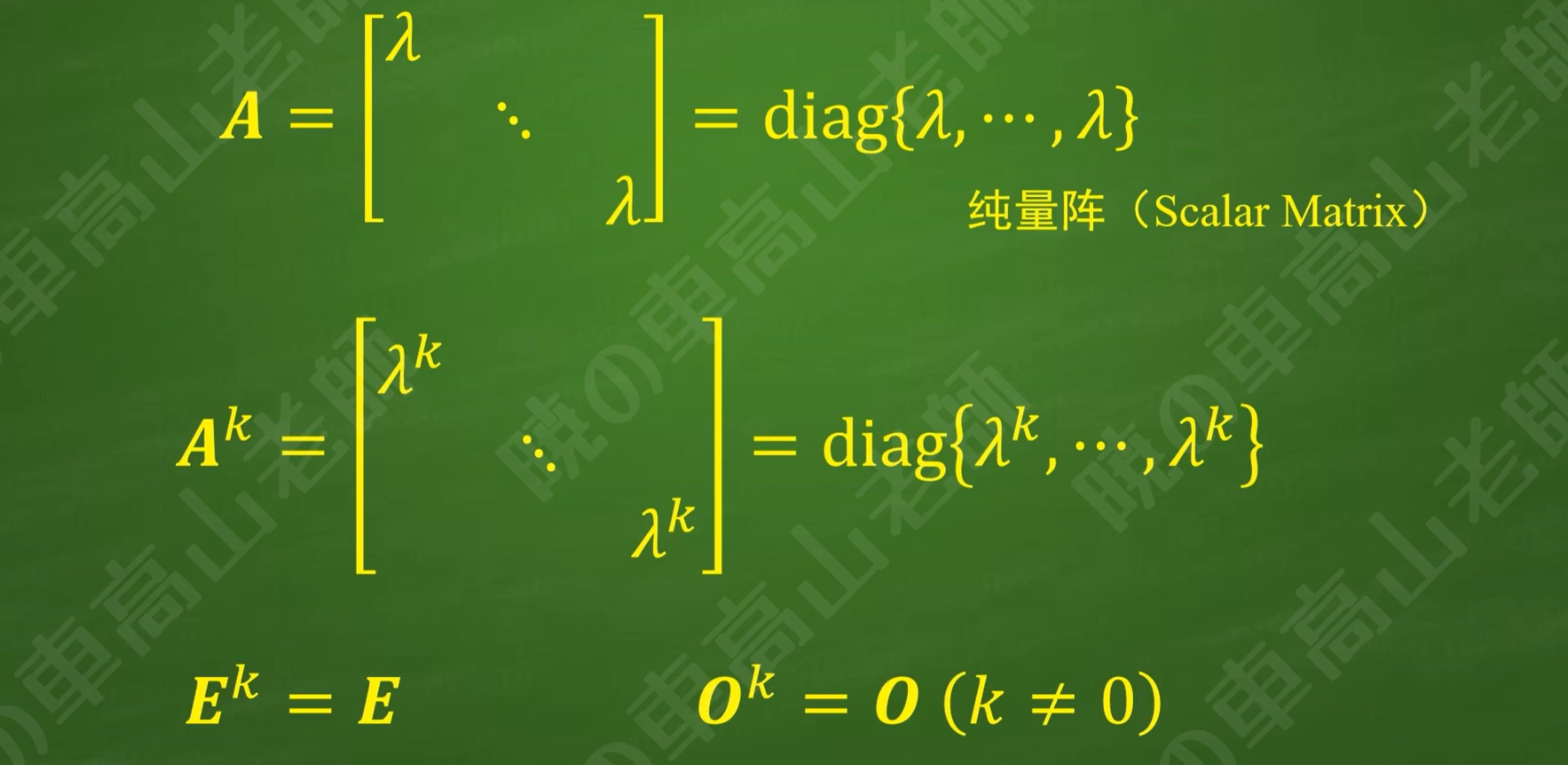
5.内容总结

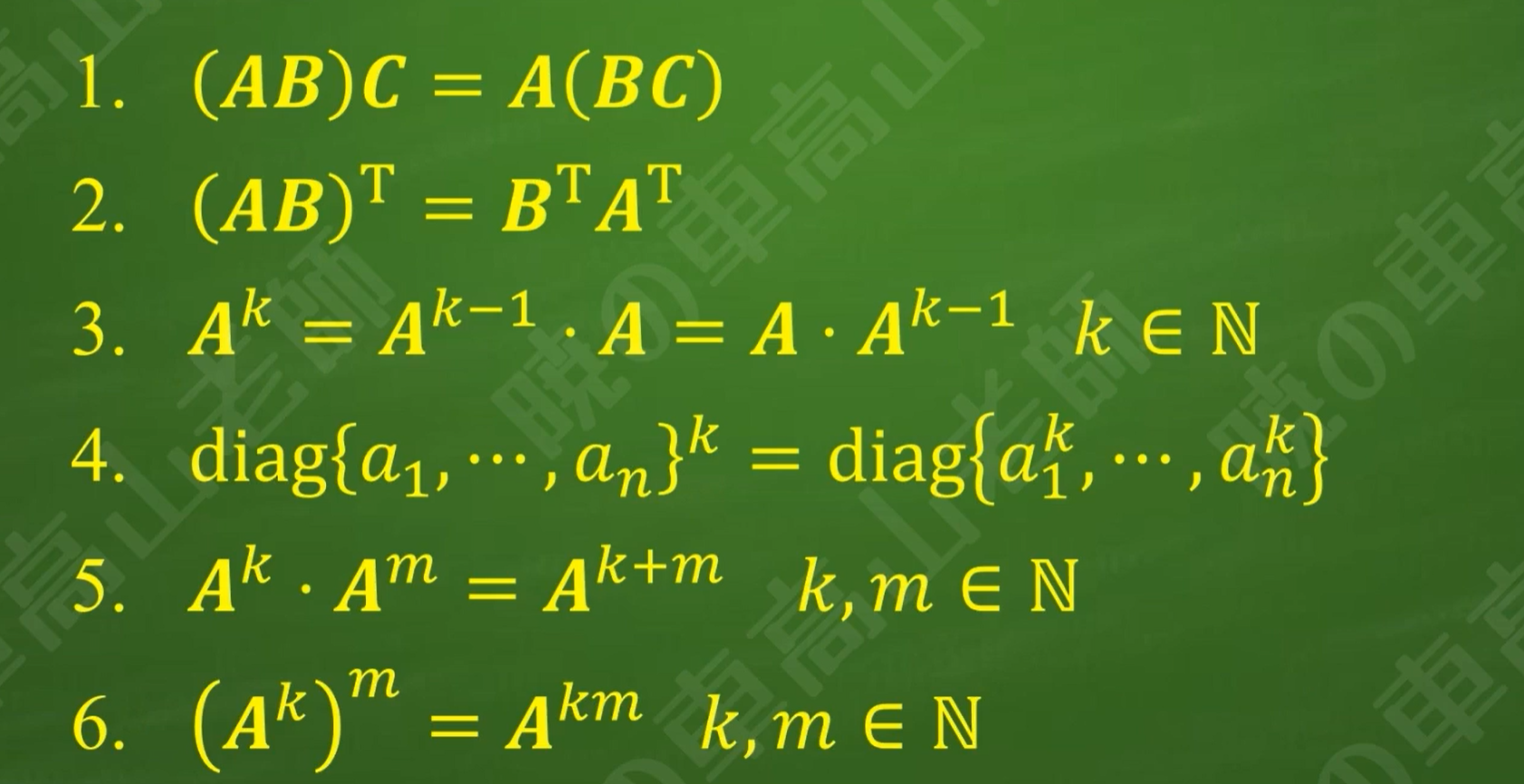
内容较多，需要复习巩固