洛谷 P1551 亲戚

 题目链接：亲戚 - 洛谷

题目详情：

若某个家族人员过于庞大，要判断两个是否是亲戚，确实还很不容易，现在给出某个亲戚关系图，求任意给出的两个人是否具有亲戚关系。规定：x 和 y 是亲戚，y 和 z 是亲戚，那么 x 和 z 也是亲戚。如果 x，y 是亲戚，那么 x 的亲戚都是 y 的亲戚，y 的亲戚也都是 x 的亲戚。

输入格式：

第一行：三个整数 n,m,p，（n,m,p ≤ 5000），分别表示有 n 个人，m 个亲戚关系，询问 p 对亲戚关系。

以下 m 行：每行两个数 M i，M j，1 ≤ M i, M j ≤ N，表示 M i​ 和 M j​ 具有亲戚关系。

接下来 p 行：每行两个数 P i，P j​，询问 P i​ 和 P j​ 是否具有亲戚关系。

输出格式：

p 行，每行一个 Yes 或 No。表示第 i 个询问的答案为“具有”或“不具有”亲戚关系。

输入输出样例：

输入 #1

6 5 3
1 2
1 5
3 4
5 2
1 3
1 4
2 3
5 6

输出 #1

Yes
Yes
No

题目分析：

比较基础的一道并查集题目，下面简单介绍一下并查集并逐步分析：

并查集主要用于处理一些不相交集合的合并问题。主要有两部分操作：1.合并：把两个不相交的集合合并为一个集合；2.查找：查找两个元素是否在同一个集合里。

初始化：

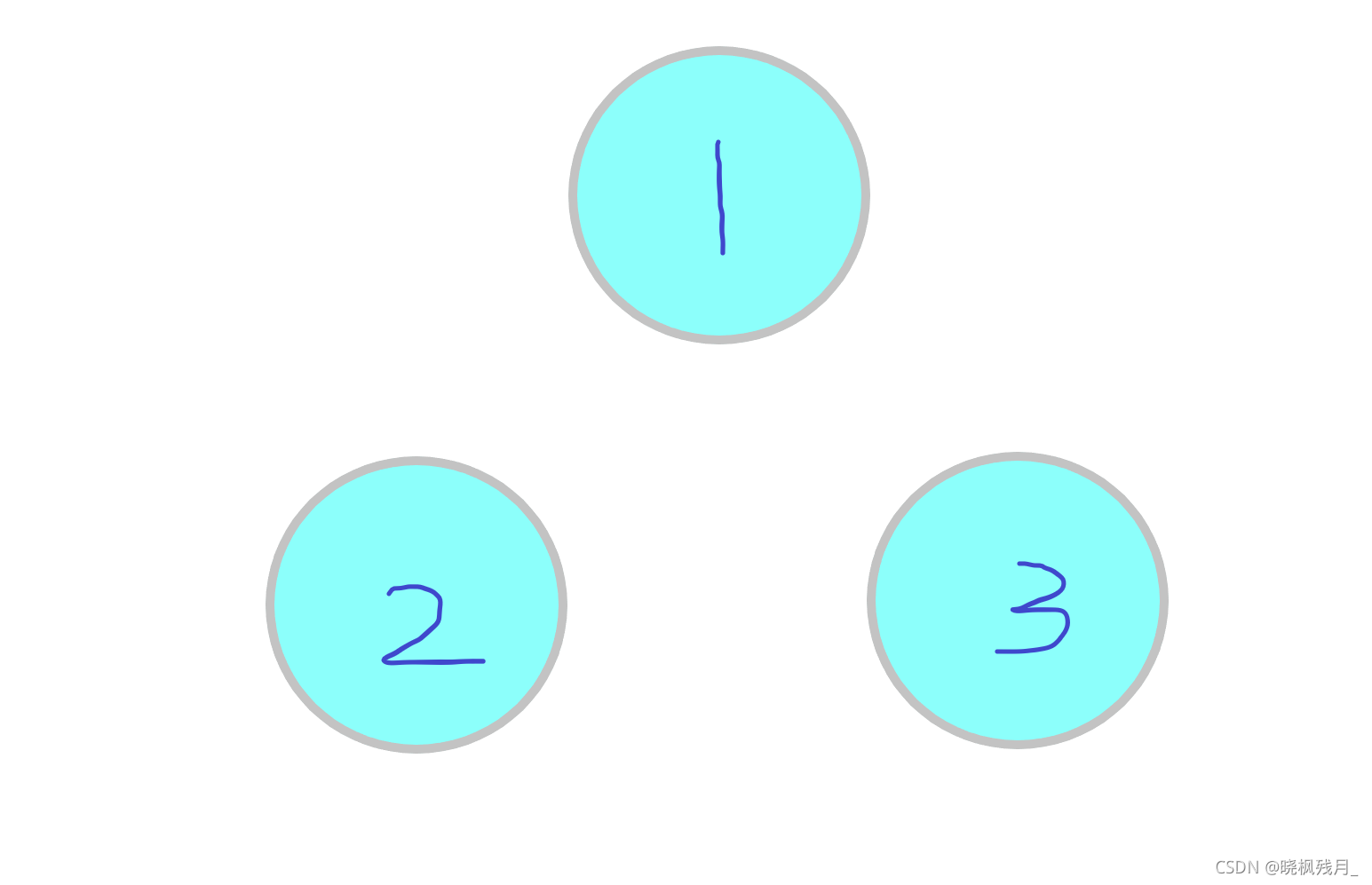
#define max 10001
int fa[max];//用数组来储存集合元素
void init_set(int n)//将n个元素设为n个独立的集合
{
    for (int i = 1; i <= n; i++)
    {
        fa[i] = i;
    }
}

图解（1，2，3初始化为3个独立的集合） 

本题中先初始化将每个人的祖先设置为自己，每人单独为一个集合。

合并：

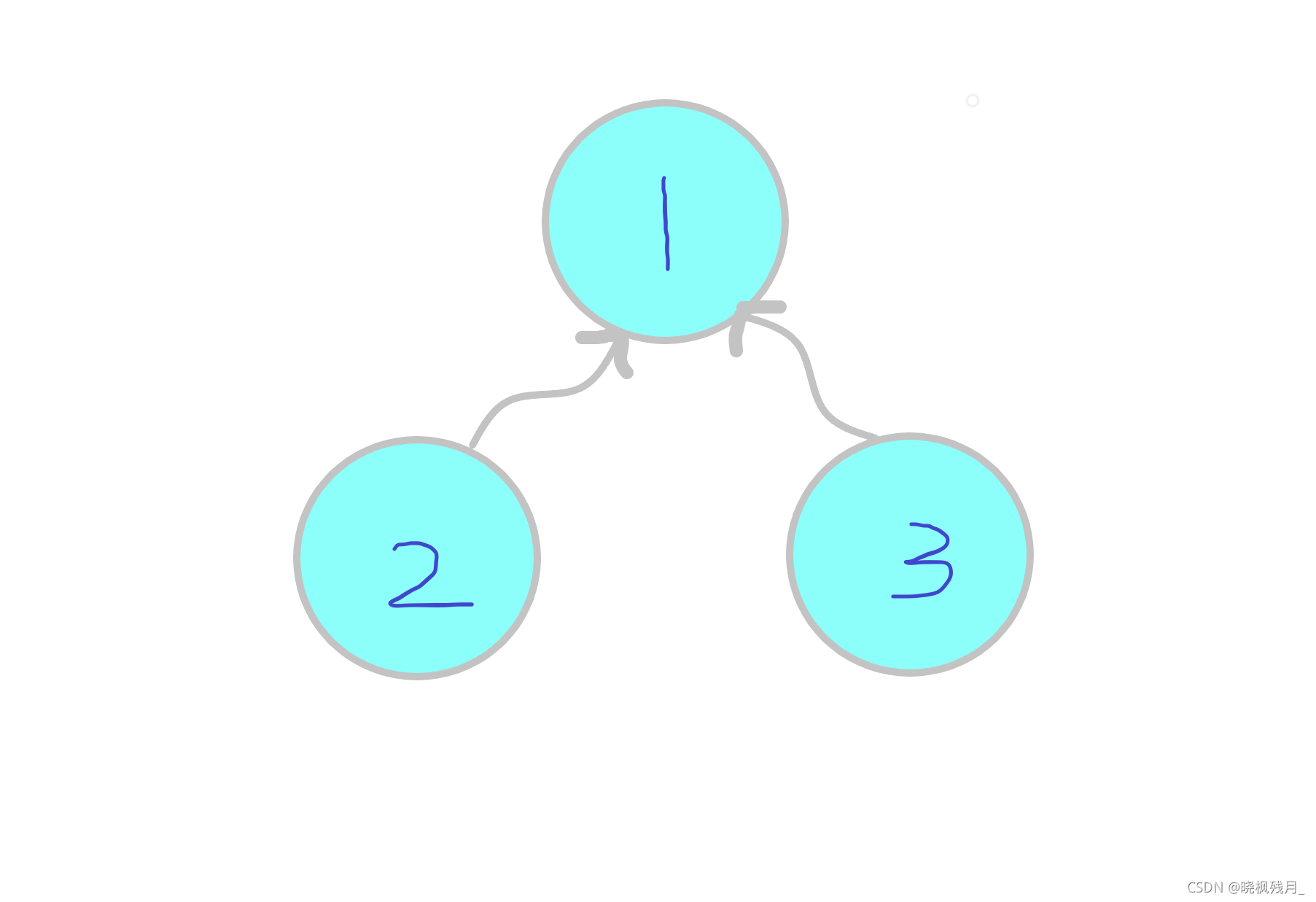
void union_set(int i, int j)//将j合并到i的集合中
{
    fa[find_set(i)] = find_set(j);//find_set为查找部分函数
}

图解（将 2 和 3 合并到 1 集合中形成树形结构，其中1为树的根节点） 

 本题中将输入的m行中具有亲戚关系的两人合并为1个集合（将两人的祖先合并，设后一个人的祖先是前面的那个人）。

查找：

int find_set(int x)//查找
{
    if (fa[x] == x)//元素的值和集相等
        return x;
    else
        return find_set(fa[x]);//继续访问父节点
}

本题中不断查找判断两人的祖先（根节点）是否相同，然后再输出判断结果。

因为初始查找的效率比较低，我们会在返回时顺便把x所属的集改成根节点，每个元素到根节点的路径就缩短了。

查找—路径压缩（递归版本）：

int find_set(int x)//查找-路径压缩
{
    if(fa[x] == x)
        return x;
    else
    {
        fa[x] = find_set(fa[x]);//父节点设为根节点
        return fa[x];
    }
}

简写（整体代码中引用此简写的查找代码）：

int find_set(int x)//查找
{
    return fa[x] == x ? x : (fa[x] = find_set(fa[x]));//如果？前面条件成立返回x，否则返回fa[x] = find_set(fa[x])
}

查找—路径压缩（非递归版本如果担心数据规模太大爆栈可以用非递归版）：

int find_set(int x)//查找-路径压缩
{
    int r = x;
    while (fa[r] != r)//找到根节点
    {
        r = fa[r];
    }
    int i = x, j;
    while (i != r)
    {
        j = fa[i];//用临时变量j记录
        fa[i] = r;//把路径上元素的集改为根节点
        i = j;
    }
    return r;
}

c++完整代码（已ac）：

#include <iostream>
using namespace std;
#define max 5001
int fa[max];
void init_set(int n)//将n个元素设为n个独立的集合
{
    for (int i = 1; i <= n; i++)
    {
        fa[i] = i;
    }
}
int find_set(int x)//查找
{
    return fa[x] == x ? x : (fa[x] = find_set(fa[x]));
}
void union_set(int i, int j)//合并
{
    fa[find_set(i)] = find_set(j);//将i和j的祖先合并
}
int main()
{
    int n, m, p, x, y;
    cin >> n >> m >> p;
    init_set(n);//家族人数读入
    for (int i = 0; i < m; i++)//将有亲戚关系的进行合并
    {
        cin >> x >> y;
        union_set(x, y);
    }
    for (int i = 0; i < p; i++)
    {
        cin >> x >> y;
        if (find_set(x) == find_set(y))//双方是亲戚
        {
            cout << "Yes" << endl;
        }
        else
        {
            cout << "No" << endl;
        }
    }
    return 0;
}

计算机204 zjr