《算法图解》第一、二章

• 大O算法：反映了最坏情况下算法运行速度。

1. 算法的速度指的并非是时间，而是操作数的增速。
2. 谈论算法的速度时，我们说的是随着输入的增加，其运行时间将以什么样的速度增加。
3. O(log n)比O(n))快，当需要搜索的元素越多时，前者比后者快得越多。

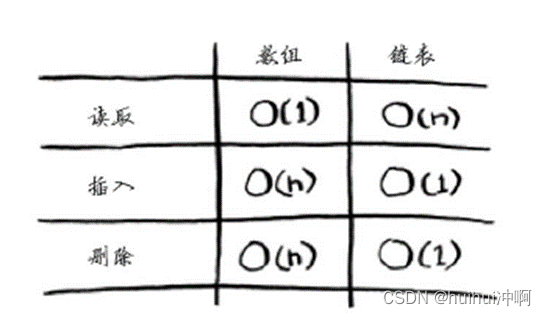
• 数组和链表

1. 数组：额外请求的位置无法使用，浪费内存。元素位置连续，当内存分配不够还要转移。
2. 链表：使用链表时，根本就不需要移动元素，只要有足够内存，就能为链表分配内存。
3. 链表只能顺序访问，数组支持随机访问。

   

 

• 二分查找

1. 简介：其输入是一个有序的元素列表（必须有序的原因稍后解释）。如果要 查找的元素包含在列表中，二分查找返回其位置；否则返回null。算法运行时间：
2. 代码实现

def binary_search(list,item):
    low = 0
    high = len(list)-1
    while low <= high:
        mid = int((low+high)/2)
        guess = list[mid]
        if guess == item:
            return mid
        if guess > item:
            high = mid-1
        else:
            low = mid+1
    return None
my_list = [1,3,5,7,9]
print(binary_search(my_list,3))
print(binary_search(my_list,-1))

• 2.选择排序

1. 简介：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。 以此类推，直到全部待排序的数据元素的个数为零。算法运行时间：

2.  代码实现

def findsmallest(arr):
    smallest = arr[0]
    smallest_index = 0
    for i in range(1,len(arr)):
        if arr[i] < smallest:
            smallest = arr[i]
            smallest_index = i
    return smallest,smallest_index

def selectionSort(arr):
    new_arr = []
    for i in range(len(arr)):
        smallest,smallest_index= findsmallest(arr)
        new_arr.append(arr[smallest_index])
        arr.remove(smallest)
    return new_arr

print(selectionSort([5, 3, 6, 2, 10]))