第二章 空间向量代数(Chapter 2 Spatial Vector Algebra)
空间矢量是结合了刚体运动和力的线性和角度方面的 6D 矢量。空间矢量为研究刚体动力学提供了一种简洁的符号,在这种符号中,一个空间矢量可以完成两个三维矢量的工作,一个空间方程可以取代两个(有时是多个 )三维矢量方程。空间矢量符号使我们能够快速建立运动方程,并以符号 形式简洁地表达出来。空间矢量符号还能让我们快速推导出动力学算法, 并以简洁的形式表达出来,便于转换成高效的计算机代码。
本章介绍空间向量代数的第一原理,直至单个刚体的运动方程。本章还介绍了平面向量代数,它是空间向量代数对只在二维平面内运动的刚体的调整。附录 A 介绍了空间向量运算的实现方法;第 3 章介绍了如何使用 空间向量分析一般刚体系统。
2.1 数学前言(Mathematical Preliminaries)
本节简要回顾空间向量代数中使用的一些数学概念和符号。更多详情可参阅 Green- wood (1988)、Selig (1996) 等书籍。 向量和向量空间:线性代数将向量定义为向量空间的元素;不同种类的向量是不同向量空间的元素。在本书中经常出现的有四个向量空间,它们被赋予了特殊的名称:
Rn−坐标向量−coordinate vectorsEn−欧氏向量−Euclidean vectorsMn−空间运动矢量−spatial motion vectorsFn−空间力矢量−spatial force vectors
\mathrm{R}^n - 坐标向量 - coordinate \ vectors \\
\mathrm{E}^n - 欧氏向量 - Euclidean \ vectors \\
\mathrm{M}^n - 空间运动矢量 - spatial \ motion \ vectors \\
\mathrm{F}^n - 空间力矢量 - spatial \ force\ vectors
Rn−坐标向量−coordinate vectorsEn−欧氏向量−Euclidean vectorsMn−空间运动矢量−spatial motion vectorsFn−空间力矢量−spatial force vectors
在每种情况下,上标表示维数。还有一个经常出现的空间是 m×nm \times nm×n 矩阵空间,表示为 Rm×n\mathrm{R}^{m \times n}Rm×n 。
坐标向量是实数的 nnn-tuple,或者以矩阵形式表示, n×1n \times 1n×1 个实数矩阵( 即列向量)。坐标向量通常代表其他向量;我们使用抽象向量(abstract vector)一词来指代被代表的向量。欧几里得向量有一个特殊的性质,即在向量上定义了一个欧几里得内积。这个积赋予了向量的大小和方向属性。用于描述刚体动力学的三维向量就是欧几里得向量。空间矢量不是欧几里得矢量, 而是一对矢量空间的元素:一个用于运动矢量,一个用于力矢量。空间运动矢量描述刚体运动的属性,如速度和加速度,而空间力矢量则描述力、冲量和动量。M6\mathrm{M}^6M6 和 F6\mathrm{F}^6F6 这两个空间是本章的主要内容。
**帽子和下划线(Hats and Underlines):**当空间矢量和三维矢量同时出现时,我们会用帽子( 如 v^\hat{\boldsymbol{v}}v^、f^\hat{\boldsymbol{f}}f^)标记一些空间矢量,以避免它们与三维矢量同时出现时产生命名冲突。同样,我们通常不区分坐标向量和它们所代表的抽象向量,但如果需要区分,我们会在坐标向量下划线( 例如 v‾\underline{\boldsymbol{v}}v 代表 v\boldsymbol{v}v)。我们只在需要的地方使用这些符号, 在本章之外几乎不使用。
向量空间的对偶(The Dual of a Vector Space): 设 VVV 是一个向量空间。它的对偶空间,记为 V∗V^*V∗ , 是一个维度与 VVV 相同的向量空间,并且具有在它和 VVV 之间定义标量积的特性(即标量积从每个空间各取一个参数)。如果 u∈V∗\boldsymbol{u} \in V^*u∈V∗ 和 v∈V\boldsymbol{v} \in Vv∈V,那么这 个标量积可以写成 u⋅v\boldsymbol{u} \cdot \boldsymbol{v}u⋅v 或 v⋅u\boldsymbol{v} \cdot \boldsymbol{u}v⋅u,两个表达式的含义相同。对偶性是一 种对称关系:如果 U=V∗U=V^*U=V∗ ,那么 V=U∗V=U^*V=U∗ 。
对偶性概念与空间向量代数有关,因为空间 Mn\mathrm{M}^nMn 和 Fn\mathrm{F}^nFn 是对偶的(即每个空间都是另一个空间的对偶)。特别是,运动矢量和力矢量之间定义了一个标量积,即如果 m∈M6\boldsymbol{m} \in \mathrm{M}^6m∈M6 描述了一个刚体的速度,而 f∈F6\boldsymbol{f} \in \mathrm{F}^6f∈F6 描述了 作用在刚体上的力,那么 m⋅f\boldsymbol{m} \cdot \boldsymbol{f}m⋅f 就是力传递的功率。
向量空间与其对偶空间之间的标量积必须是非退化的(nondegenerate)(也称为非奇异的(nonsingular))。如果标量积具有以下性质,那么它就是非奇异的:对于任意 v∈V\boldsymbol{v} \in Vv∈V ,如果 v≠0\boldsymbol{v} \neq \mathbf{0}v=0,那么至少存在一个 u∈V∗\boldsymbol{u} \in V^*u∈V∗ 的向量满足 v⋅u≠0\boldsymbol{v} \cdot \boldsymbol{u} \neq 0v⋅u=0 。这个性质是保证 VVV 和 V∗V^*V∗ 上存在对偶基的充分条件。
对偶基(Dual Bases):假设我们有两个向量空间 UUU 和 VVV,使得 U=V∗U=V^*U=V∗ 。让D={d1,…,dn}\mathcal{D}=\left\{\boldsymbol{d}_1, \ldots, \boldsymbol{d}_n\right\}D={d1,…,dn} 是 UUU 的基,让 E={e1,…,en}\mathcal{E}=\left\{\boldsymbol{e}_1, \ldots, \boldsymbol{e}_n\right\}E={e1,…,en} 是 VVV 的基 。如果它们满足下面互换条件(eciprocity condition),则构成UUU 和VVV的对偶基(dual basis):
di⋅ej={1 if i=j0 otherwise
\boldsymbol{d}_i \cdot \boldsymbol{e}_j= \begin{cases}1 & \text { if } i=j \\ 0 & \text { otherwise }\end{cases}
di⋅ej={10 if i=j otherwise
这就是所谓的互易条件。如果 D\mathcal{D}D 和 E\mathcal{E}E 满足这个条件,则每个都是另一个的倒数。如果给定一个基,那么另一个基由互易条件唯一决定 。我们可以使用符号 D∗\mathcal{D}^*D∗ 表示 D\mathcal{D}D 的倒数。请注意,对偶基由两组基向量组成,并覆盖两个向量空间。
如果 U=EnU=\mathrm{E}^nU=En ,那么就可以设 V=UV=UV=U,这样 D\mathcal{D}D 和 E\mathcal{E}E 就成为同一个向量空间的基。还可以找到具有 D=E\mathcal{D}=\mathcal{E}D=E 特性的 D\mathcal{D}D 的特例。因此,正交基是对偶基的特例,其中 U=V=EnU=V=\mathrm{E}^nU=V=En 且 D=E\mathcal{D}=\mathcal{E}D=E 。
对偶坐标系(Dual Coordinates): 一对对偶基定义了一个对偶坐标系。我们始终使用对偶坐标系来表示空间向量;另外,我们主要使用普吕克坐标系(Plücker coordinates),它是一个特别方便的对偶坐标系的选择。对偶坐标系有一个特殊性质:
u⋅v=u‾Tv‾,
\boldsymbol{u} \cdot \boldsymbol{v}=\underline{\boldsymbol{u}}^{\mathrm{T}} \underline{\boldsymbol{v}},
u⋅v=uTv,
其中,u‾\underline{\boldsymbol{u}}u 和 v‾\underline{\boldsymbol{v}}v 是坐标向量,代表由 D\mathcal{D}D 和 E\mathcal{E}E 定义的对偶坐标系中的 u∈U\boldsymbol{u} \in Uu∈U 和 v∈V\boldsymbol{v} \in Vv∈V 。一个直接的推论是,u‾\underline{\boldsymbol{u}}u 和 v‾\underline{\boldsymbol{v}}v 中的每个元素可以表示为
ui=ei⋅u and vi=di⋅v.
u_i=\boldsymbol{e}_i \cdot \boldsymbol{u} \quad \text { and } \quad v_i=\boldsymbol{d}_i \cdot \boldsymbol{v} .
ui=ei⋅u and vi=di⋅v.
要执行从一个对偶坐标系到另一个对偶坐标系的坐标变换,我们需要两个变换矩阵:一个对 u‾\underline{\boldsymbol{u}}u 进行操作,一个对 v‾\underline{\boldsymbol{v}}v 进行操作。如果 X\boldsymbol{X}X 是对 u‾\underline{\boldsymbol{u}}u 执行所需坐标变换的矩阵,则该矩阵对 v‾\underline{\boldsymbol{v}}v 执行相同的操作,记为 X∗\boldsymbol{X}^*X∗,两个矩阵通过以下方程相关联
X∗=X−T.
\boldsymbol{X}^*=\boldsymbol{X}^{-\mathrm{T}} .
X∗=X−T.
这个关系可由条件得出:对于所有的 u‾\underline{\boldsymbol{u}}u 和v‾\underline{\boldsymbol{v}}v, u‾Tv‾=(Xu‾)T(X∗v‾)\underline{\boldsymbol{u}}^{\mathrm{T}} \underline{\boldsymbol{v}}=(\boldsymbol{X} \underline{\boldsymbol{u}})^{\mathrm{T}}\left(\boldsymbol{X}^* \underline{\boldsymbol{v}}\right)uTv=(Xu)T(X∗v) 。
a⋅\boldsymbol{a} \cdota⋅ 和a× \boldsymbol{a} \times \mathbf{\text { }}a× 操作: 可以将像 a⋅b\boldsymbol{a} \cdot \boldsymbol{b}a⋅b 和a×b\boldsymbol{a} \times \boldsymbol{b}a×b 这样的表达式解释为将运算符 a⋅\boldsymbol{a} \cdota⋅ 或a×\boldsymbol{a} \timesa× 应用与操作数 b\boldsymbol{b}b 中。因此, a⋅\boldsymbol{a} \cdota⋅ 是将 b\boldsymbol{b}b 映射到标量 a⋅b\boldsymbol{a} \cdot \boldsymbol{b}a⋅b 的运算符,而 a×\boldsymbol{a} \times \operatorname{}a× 是将 b\boldsymbol{b}b 映射到a×b\boldsymbol{a} \times \boldsymbol{b}a×b 的运算符。 如果 a\boldsymbol{a}a 是坐标向量,则 a⋅=aT\boldsymbol{a} \cdot=\boldsymbol{a}^{\mathrm{T}}a⋅=aT,且 a×\boldsymbol{a} \timesa× 是一个方阵。 a×\boldsymbol{a} \timesa× 的一些属性列于表2.1 和 2.3中。表2.3 还列出了算子 a×∗\boldsymbol{a} \times{ }^*a×∗的属性,它是 a×\boldsymbol{a} \timesa×的对偶。
双积( Dyads and Dyadics):$\boldsymbol{a} \ \boldsymbol{b} \cdot $ 形式的表达式称为 dyad。它是一个将向量映射到向量的线性运算符。特别地,$\boldsymbol{a} \ \boldsymbol{b} \cdot $ 会将向量 c\boldsymbol{c}c 映射到向量 a(b⋅c)\boldsymbol{a}(\boldsymbol{b} \cdot \boldsymbol{c})a(b⋅c),它是 a\boldsymbol{a}a 的标量倍数。如果 a‾\underline{\boldsymbol{a}}a 和 b‾\underline{\boldsymbol{b}}b 是表示 a\boldsymbol{a}a 和 b 的坐标向量,则$\boldsymbol{a} \ \boldsymbol{b} \cdot $ 由矩阵 a‾ b‾T\underline{\boldsymbol{a}}\ \underline{\boldsymbol{b}}^{\mathrm{T}}a bT 表示,其秩为 1。在最一般的情况下,我们可以有 a∈U,b∈V\boldsymbol{a} \in U, \boldsymbol{b} \in Va∈U,b∈V 和 c∈W\boldsymbol{c} \in Wc∈W,其中对任何这些向量空间的选择没有限制,除了必须在 VVV 和 WWW 之间定义标量积。这样的dyad 从 WWW 到 UUU 映射。
A dyadic (or dyadic tensor)是一般线性向量的映射。任何 dyadic 可以表示为 rrr 个线性独立 dyads 之和:
L=∑i=1raibi⋅
\boldsymbol{L}=\sum_{i=1}^r \boldsymbol{a}_i \boldsymbol{b}_i \cdot
L=i=1∑raibi⋅
其中,ai∈U,bi∈V\boldsymbol{a}_i \in U, \boldsymbol{b}_i \in Vai∈U,bi∈V, r≤min(m,n)r \leq \min (m, n)r≤min(m,n), 其中m=dim(U)m=\operatorname{dim}(U)m=dim(U) 且 n=dim(V)n=\operatorname{dim}(V)n=dim(V). (如果向量 ai\boldsymbol{a}_iai 在 UUU 中是线性独立的,向量 bi\boldsymbol{b}_ibi 在 VVV 中是线性独立的)。 如果 ai\boldsymbol{a}_iai 和 bi\boldsymbol{b}_ibi 是坐标向量, 那么 L\boldsymbol{L}L 可以写为
L=∑i=1raibiT,
\boldsymbol{L}=\sum_{i=1}^r \boldsymbol{a}_i \boldsymbol{b}_i^{\mathrm{T}},
L=i=1∑raibiT,
这是一个秩为 rrr 的 m×nm \times nm×n 的矩阵。 如果 m=n=rm=n=rm=n=r ,则 L\boldsymbol{L}L 是一个 1:11: 11:1 的映射且是可逆的。Dyadics 与空间 惯性张量有关。
2.2 空间速度(Spatial Velocity)
让我们来计算刚体的空间速度公式。我们从刚体 BBB 开始,在空间的任一位置选择一个定点 OOO 。(见图 2.1(a))。给定 OOO,则刚体 BBB 的速度可由一对三维矢量指定:当前与 OOO 重合的刚体定点的线速度 vO\boldsymbol{v}_OvO 和角速度 矢量 ω\boldsymbol{\omega}ω。因此,可以将刚体整体视为以线速度 vO\boldsymbol{v}_OvO 平移,同时以角速度 ω\boldsymbol{\omega}ω 绕通过 OOO 的轴线旋转。 根据这一描述,我们可以用公式计算出刚体中任意一点的速度
vP=vO+ω×OP→(2.1)
\boldsymbol{v}_P=\boldsymbol{v}_O+\boldsymbol{\omega} \times \overrightarrow{O P} \tag{2.1}
vP=vO+ω×OP(2.1)
其中,PPP 是观测点,vP\boldsymbol{v}_PvP 是刚体的中的一个固定点 PPP 的速度,OP→\overrightarrow{O P}OP 给出了 PPP 相对于 OOO 的位置。这个方程清晰地展示了 vP\boldsymbol{v}_PvP 由两项组成:一项是刚体整体平移造成的 vO\boldsymbol{v}_OvO, 另一项是由于刚体绕定点 OOO 旋转以角速度 ω\boldsymbol{\omega}ω 造成的。
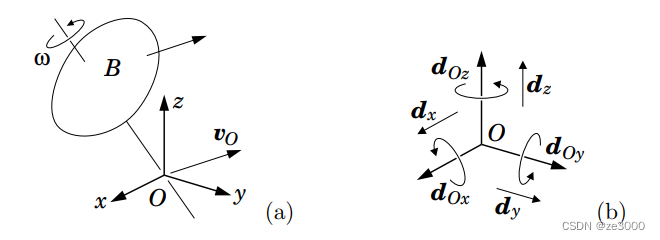
虽然每一项都取决于点 OOO 的位置,但它们的总和并不取决于点 OOO 的位置(即依赖关系抵消),因此 vP\boldsymbol{v}_PvP 只取决于刚体 BBB 的运动和 PPP 点的位置。 请注意,PPP、vP\boldsymbol{v}_PvP 和 ω\boldsymbol{\omega}ω 描述的刚体运动与 OOO、vO\boldsymbol{v}_OvO 和 ω\boldsymbol{\omega}ω 描述的刚体运动相同 。
现在我们引入一个笛卡尔坐标系 OxyzO_{x y z}Oxyz ,其原点位于 OOO。这个坐标系定义了三个相互垂直的方向,即 xxx、yyy 和 zzz,以及三条有向直线,即 Ox,OyO x, O yOx,Oy 和 OzO zOz,每条直线都经过点 OOO。这个坐标系同时也定义了一组正交基 {i,j,k}⊂E3\{\boldsymbol{i}, \boldsymbol{j}, \boldsymbol{k}\} \subset \mathrm{E}^3{i,j,k}⊂E3,我们可以用它们的笛卡尔坐标来表示 ω\boldsymbol{\omega}ω 和 vO\boldsymbol{v}_OvO :
ω=ωxi+ωyj+ωzk
\boldsymbol{\omega}=\omega_x \boldsymbol{i}+\omega_y \boldsymbol{j}+\omega_z \boldsymbol{k}
ω=ωxi+ωyj+ωzk
和
vO=vOxi+vOyj+vOzk.
\boldsymbol{v}_O=v_{O x} \boldsymbol{i}+v_{O y} \boldsymbol{j}+v_{O z} \boldsymbol{k} .
vO=vOxi+vOyj+vOzk.
将 ω\boldsymbol{\omega}ω 和 vO\boldsymbol{v}_OvO 分解到对应的坐标系,我们可以将 BBB 的速度描述为六个基本运动的总和:绕直线 OxO xOx旋转 ωx\omega_xωx ,绕 OyO yOy 旋转ωy\omega_yωy ,绕 OzO zOz 旋转 ωz\omega_zωz ,以及分别沿 xxx、yyy 和 zzz 方向平移 vOx,vOyv_{O x}, v_{O y}vOx,vOy 和vOzv_{O z}vOz 。
我们的目标是得到一个空间速度矢量,v^∈M6\hat{\boldsymbol{v}} \in \mathrm{M}^6v^∈M6 ,它描述的运动与 ω\boldsymbol{\omega}ω 和 vO\boldsymbol{v}_OvO 相同。我们可以通过首先定义 M6\mathrm{M}^6M6的基,然后在该基上计算出 v^\hat{\boldsymbol{v}}v^ 的坐标来。我们将使用的基是
DO={dOx,dOy,dOz,dx,dy,dz}⊂M6,(2.2)
\mathcal{D}_O=\left\{\boldsymbol{d}_{O x}, \boldsymbol{d}_{O y}, \boldsymbol{d}_{O z}, \boldsymbol{d}_x, \boldsymbol{d}_y, \boldsymbol{d}_z\right\} \subset \mathrm{M}^6, \tag{2.2}
DO={dOx,dOy,dOz,dx,dy,dz}⊂M6,(2.2)
如图 2.1(b)所示。这就是所谓的普吕克基(Plücker basis),它定义了 M6\mathrm{M}^6M6 上的普吕克坐标系。前三个基向量 dOx\boldsymbol{d}_{O x}dOx, dOy\boldsymbol{d}_{O y}dOy 和 dOz\boldsymbol{d}_{O z}dOz分别是绕直线 OxO xOx, OyO yOy 和 OzO zOz 的方向旋转,其余的分别是在 xxx、yyy 和 zzz 方向上的单位平移。将这些基向量的定义与刚才描述的六个基本运动进行比较,可以立即得出以下结论
v^=ωxdOx+ωydOy+ωzdOz+vOxdx+vOydy+vOzdz(2.3)
\hat{\boldsymbol{v}}=\omega_x \boldsymbol{d}_{O x}+\omega_y \boldsymbol{d}_{O y}+\omega_z \boldsymbol{d}_{O z}+v_{O x} \boldsymbol{d}_x+v_{O y} \boldsymbol{d}_y+v_{O z} \boldsymbol{d}_z \tag{2.3}
v^=ωxdOx+ωydOy+ωzdOz+vOxdx+vOydy+vOzdz(2.3)
因此,v^\hat{\boldsymbol{v}}v^ 在 DO\mathcal{D}_ODO 中的 Plücker coordinates 就是 ω\boldsymbol{\omega}ω 和 vO\boldsymbol{v}_OvO 在 {i,j,k}\{\boldsymbol{i}, \boldsymbol{j}, \boldsymbol{k}\}{i,j,k} 中的笛卡尔坐标。右边的每个项都取决于 OxyzO_{x y z}Oxyz 的位置和方向,但可以证明整个表达式是不变的。(见例 2.2)。在 DO\mathcal{D}_ODO 坐标中表示 v^\hat{\boldsymbol{v}}v^ 的坐标向量可以写成
v^‾O=[ωxωyωzvOxvOyvOz]=[ω‾v‾O],(2.4)
\boldsymbol{\underline{\hat{v}}}_O=\left[\begin{array}{c}
\omega_x \\
\omega_y \\
\omega_z \\
v_{O x} \\
v_{O y} \\
v_{O z}
\end{array}\right]=\left[\begin{array}{c}
\underline{\boldsymbol{\omega}} \\
\underline{\boldsymbol{v}}_O
\end{array}\right], \tag{2.4}
v^O=ωxωyωzvOxvOyvOz=[ωvO],(2.4)
其中最右边的表达式是一种方便的紧凑符号,其中 6D 坐标向量表示为两个 三维坐标向量 ω‾=[ωx ωy ωz]T\underline{\boldsymbol{\omega}}=\left[\omega_x\ \omega_y\ \omega_z\right]^{\mathrm{T}}ω=[ωx ωy ωz]T 和 v‾O=[vOx vOy vOz]T\underline{\boldsymbol{v}}_O=\left[v_{O x}\ v_{O y} \ v_{O z}\right]^{\mathrm{T}}vO=[vOx vOy vOz]T 的连接。
例 2.1 等式 2.1 将向量 vP\boldsymbol{v}_PvP 与空间中的每个点 PPP 联系起来。因此,它定义 了一个矢量场–刚体 BBB 的速度场。我们可以将这个方程写成这种形式
V(P)=vO+ω×OP→,(2.5)
\boldsymbol{V}(P)=\boldsymbol{v}_O+\boldsymbol{\omega} \times \overrightarrow{O P}, \tag{2.5}
V(P)=vO+ω×OP,(2.5)
其中 V\boldsymbol{V}V 表示向量场,V(P)\boldsymbol{V}(P)V(P) 表明 V\boldsymbol{V}V 是与点 PPP 关联的向量。虽然 OOO 出现在 V\boldsymbol{V}V 的定义中,但右侧相对于 OOO 的位置是不变的,因此场本身与 OOO 无关。空间向量和向量场之间的这种联系可以帮助人们直观地了解空间向量的真正含义以及空间向量表达式的真正含义。例如,假设 v^1\hat{\boldsymbol{v}}_1v^1 和 v^2\hat{\boldsymbol{v}}_2v^2 是两个空间速度,V1\boldsymbol{V}_1V1 和 V2\boldsymbol{V}_2V2 是相应的矢量场。如果 v^sum =v^1+v^2\hat{\boldsymbol{v}}_{\text {sum }}=\hat{\boldsymbol{v}}_1+\hat{\boldsymbol{v}}_2v^sum =v^1+v^2,则对应于 v^sum \hat{\boldsymbol{v}}_{\text {sum }}v^sum 的向量场对于所有 PPP 具有属性 Vsum (P)=V1(P)+V2(P)\boldsymbol{V}_{\text {sum }}(P)=\boldsymbol{V}_1(P)+\boldsymbol{V}_2(P)Vsum (P)=V1(P)+V2(P)。
例 2.2 让我们研究方程2.3相对于原点选择的不变性。我们可以通过定义 v^′\hat{\boldsymbol{v}}^{\prime}v^′ 为以 PPP 点为原点获得的空间速度,并证明 v^′=v^\hat{\boldsymbol{v}}^{\prime}=\hat{\boldsymbol{v}}v^′=v^ 来实现这一点。因此 v^′\hat{\boldsymbol{v}}^{\prime}v^′ 的表达式为
v^′=ωxdPx+ωydPy+ωzdPz+vPxdx+vPydy+vPzdz,
\hat{\boldsymbol{v}}^{\prime}=\omega_x \boldsymbol{d}_{P x}+\omega_y \boldsymbol{d}_{P y}+\omega_z \boldsymbol{d}_{P z}+v_{P x} \boldsymbol{d}_x+v_{P y} \boldsymbol{d}_y+v_{P z} \boldsymbol{d}_z,
v^′=ωxdPx+ωydPy+ωzdPz+vPxdx+vPydy+vPzdz,
我们要做的事是将这个表达式与方程2.3等同起来。为了简单起见,我们选择 PPP 相对于 OxyzO_{xyz}Oxyz 的坐标为 (r,0,0)(r, 0, 0)(r,0,0),如图 2.2 所示。在这种情况下,线速度坐标由等式2.1给出。
[vPxvPyvPz]=v‾O+ω‾×[r00]=[vOxvOy+ωzrvOz−ωyr];
\left[\begin{array}{l}
v_{P x} \\
v_{P y} \\
v_{P z}
\end{array}\right]=\underline{\boldsymbol{v}}_O+\underline{\boldsymbol{\omega}} \times\left[\begin{array}{l}
r \\
0 \\
0
\end{array}\right]=\left[\begin{array}{c}
v_{O x} \\
v_{O y}+\omega_z r \\
v_{O z}-\omega_y r
\end{array}\right] ;
vPxvPyvPz=vO+ω×r00=vOxvOy+ωzrvOz−ωyr;
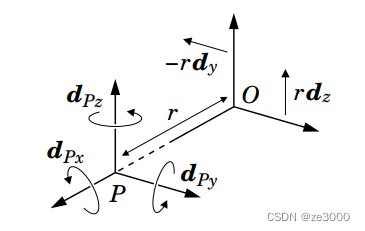
图2.2 dPy\boldsymbol{d}_{P y}dPy 和 dPz\boldsymbol{d}_{P z}dPz 在 OOO 点处的表达
PPP 的三个基向量是
dPx=dOx,dPy=dOy+rdz,dPz=dOz−rdy.
\begin{aligned}
& \boldsymbol{d}_{P x}=\boldsymbol{d}_{O x}, \\
& \boldsymbol{d}_{P y}=\boldsymbol{d}_{O y}+r \boldsymbol{d}_z, \\
& \boldsymbol{d}_{P z}=\boldsymbol{d}_{O z}-r \boldsymbol{d}_y .
\end{aligned}
dPx=dOx,dPy=dOy+rdz,dPz=dOz−rdy.
将上面三个方程组合,得到:
v^′=ωxdOx+ωy(dOy+rdz)+ωz(dOz−rdy)+vOxdx+(vOy+ωzr)dy+(vOz−ωyr)dz,
\begin{aligned}
\hat{\boldsymbol{v}}^{\prime}= & \omega_x \boldsymbol{d}_{O x}+\omega_y\left(\boldsymbol{d}_{O y}+r \boldsymbol{d}_z\right)+\omega_z\left(\boldsymbol{d}_{O z}-r \boldsymbol{d}_y\right) \\
& +v_{O x} \boldsymbol{d}_x+\left(v_{O y}+\omega_z r\right) \boldsymbol{d}_y+\left(v_{O z}-\omega_y r\right) \boldsymbol{d}_z,
\end{aligned}
v^′=ωxdOx+ωy(dOy+rdz)+ωz(dOz−rdy)+vOxdx+(vOy+ωzr)dy+(vOz−ωyr)dz,
该式与式2.3 等价。
回到三个基向量,我们有 dPx=dOx\boldsymbol{d}_{P x}=\boldsymbol{d}_{O x}dPx=dOx,因为两条线 PxP xPx 和 OxO xOx 是相同的。为了理解 dPy\boldsymbol{d}_{P y}dPy 的表达式,想象一个刚体以单位角速度绕 PyPyPy 轴旋转,因此它的空间速度为 dPy\boldsymbol{d}_{P y}dPy。那么固定在 OOO 处的刚体在 zzz 方向上将具有大小为 $r $ 的线速度,如图 2.2 所示;因此,刚体的速度可以表示为绕线 OyO yOy 的单位角速度与 zzz 方向上大小为 rrr 的线速度之和(即 dOy+rdz\boldsymbol{d}_{O y}+r \boldsymbol{d}_zdOy+rdz)。使用 PzP zPz 重复上述步骤可得出给定的表达式对于 dPz\boldsymbol{d}_{P z}dPz。
这里提出的分析很容易扩展到 PPP 的一般位置的情况,并且可以使用类似的论证来证明等式2.3 相对于 OxyzO_{xyz}Oxyz 的方向不变。
2.3 空间力(Spatial Force)
获得了空间速度的表达式后,现在让我们对空间力进行同样的操作。给定一个任意点 OOO(可以位于空间中的任何位置),可以作用在刚体 BBB 上的最常见的力由线性力 f\boldsymbol{f}f(沿穿过 OOO 的直线作用)和力偶 nO\boldsymbol{n}_OnO 组成,它等于关于 OOO 的总矩。(见图 2.3(a)。)我们再一次得到了一个由一个任意点和两个 3D 向量组成的表示。f\boldsymbol{f}f 代替了 ω\boldsymbol{\omega}ω,nO\boldsymbol{n}_OnO 代替了 vO\boldsymbol{v}_OvO。
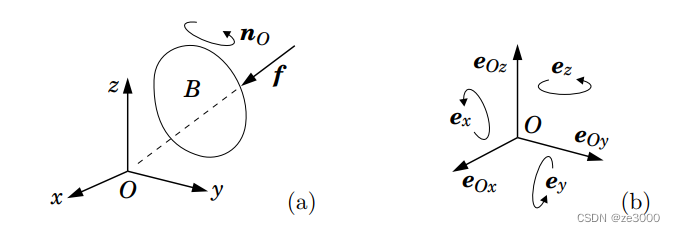
图2.3 (a)作用在刚体上的力 f\boldsymbol{f}f 和 nO\boldsymbol{n}_OnO 的表示; (b) Plücker 力坐标的基向量
给定 OOO、nO\boldsymbol{n}_OnO 和 f\boldsymbol{f}f,我们可以使用以下公式计算关于任意一点 PPP 的总矩
nP=nO+f×OP→.(2.6)
\boldsymbol{n}_P=\boldsymbol{n}_O+\boldsymbol{f} \times \overrightarrow{O P} . \tag{2.6}
nP=nO+f×OP.(2.6)
该方程是类似方程 2.1 的力矢量。它与该方程共享右侧与 OOO 的位置无关的属性。三个量 PPP、nP\boldsymbol{n}_PnP 和 f\boldsymbol{f}f 共同描述了与 OOO、nO\boldsymbol{n}_OnO 和 f\boldsymbol{f}f 相同的外加力。
现在我们引入一个笛卡尔坐标系 OxyzO_{x y z}Oxyz,其原点为 OOO,并用它来定义标准正交基 {i,j,k}∈E3\{\boldsymbol{i}, \boldsymbol{j}, \boldsymbol{k}\} \in \mathrm{E}^3{i,j,k}∈E3,以便 nO\boldsymbol{n}_OnO 和 f\boldsymbol{f}f 可以用它们的笛卡尔坐标来写:
nO=nOxi+nOyj+nOzk
\boldsymbol{n}_O=n_{O x} \boldsymbol{i}+n_{O y} \boldsymbol{j}+n_{O z} \boldsymbol{k}
nO=nOxi+nOyj+nOzk
和
f=fxi+fyj+fzk.
\boldsymbol{f}=f_x \boldsymbol{i}+f_y \boldsymbol{j}+f_z \boldsymbol{k} .
f=fxi+fyj+fzk.
将 nO\boldsymbol{n}_OnO 和 f\boldsymbol{f}f 分解为它们对应的分量后,我们可以将作用在 BBB 上的力描述为六个基本力的总和:分别在 xxx、$y $ 和 zzz 方向上的大小为 nOxn_{O x}nOx、nOyn_{O y}nOy 和 nOzn_{O z}nOz 的力偶,以及分别沿 OxO_xOx, OyO_yOy 和 OzO_zOz 的大小为 fxf_xfx 、fyf_yfy 和$ f_z$ 的线性力。该坐标系还定义了 F6\mathrm{F}^6F6 上的以下 Plücker 基:
EO={ex,ey,ez,eOx,eOy,eOz}⊂F6,
\mathcal{E}_O=\left\{\boldsymbol{e}_x, \boldsymbol{e}_y, \boldsymbol{e}_z, \boldsymbol{e}_{O x}, \boldsymbol{e}_{O y}, \boldsymbol{e}_{O z}\right\} \subset \mathrm{F}^6,
EO={ex,ey,ez,eOx,eOy,eOz}⊂F6,
如图2.3(b)所示。前三个元素是 xxx、yyy 和 $ z$ 方向上的单位力偶,其余是沿 OxO_xOx, OyO_yOy 和 OzO_zOz 线作用的单位线性力。将这些基向量的定义与刚刚描述的六个基本力进行比较,可以立即得出,如果 f^∈F6\hat{\boldsymbol{f}} \in \mathrm{F}^6f^∈F6 是表示与 OOO、nO\boldsymbol{n}_OnO 和 f\boldsymbol{f}f 相同的力的空间力向量,则
f^=nOxex+nOyey+nOzez+fxeOx+fyeOy+fzeOz.(2.8)
\hat{\boldsymbol{f}}=n_{O x} \boldsymbol{e}_x+n_{O y} \boldsymbol{e}_y+n_{O z} \boldsymbol{e}_z+f_x \boldsymbol{e}_{O x}+f_y \boldsymbol{e}_{O y}+f_z \boldsymbol{e}_{O z} . \tag{2.8}
f^=nOxex+nOyey+nOzez+fxeOx+fyeOy+fzeOz.(2.8)
此等式右侧的每个单独项都取决于 OxyzO_{x y z}Oxyz 的位置和方向,但表达式作为一个整体是不变的。因此,f^\hat{\boldsymbol{f}}f^ 的值根本不取决于 OxyzO_{x y z}Oxyz,而只取决于作用在 BBB 上的力。在 EO\mathcal{E}_OEO 坐标中表示 f^\hat{f}f^ 的坐标向量为
f^‾O=[nOxnOynOzfxfyfz]=[n‾Of‾](2.9)
\underline{\boldsymbol{\hat{f}}}_O=\left[\begin{array}{c}
n_{O x} \\
n_{O y} \\
n_{O z} \\
f_x \\
f_y \\
f_z
\end{array}\right]=\left[\begin{array}{c}
\underline{\boldsymbol{n}}_O \\
\underline{\boldsymbol{f}}
\end{array}\right] \tag{2.9}
f^O=nOxnOynOzfxfyfz=[nOf](2.9)
其中, n‾O=[nOxnOynOz]T\underline{\boldsymbol{n}}_O=\left[\begin{array}{lll}n_{O x} & n_{O y} & n_{O z}\end{array}\right]^{\mathrm{T}}nO=[nOxnOynOz]T 且 f‾=[fxfyfz]T\underline{\boldsymbol{f}}=\left[\begin{array}{lll}f_x & f_y & f_z\end{array}\right]^{\mathrm{T}}f=[fxfyfz]T.
2.4 普吕克符号(Plücker Notation)
普吕克坐标可以追溯到 19th 19^{\text {th }}19th 世纪,但基向量是新的。 它们是 6D6 \mathrm{D}6D 向量的首选坐标,部分原因是它们有助于高效的计算机实现,但主要是因为它们是最方便且易于使用的。
公式 2.4 和 2.9 中出现的符号将普吕克坐标与特定于速度和力的符号结合起来。就速度而言,我们使用两个不同的符号 (v(\boldsymbol{v}(v 和 ω)\boldsymbol{\omega})ω) 来表示 3D3 \mathrm{D}3D 矢量符号中的线速度和角速度,并在普吕克坐标表中保留了这些符号。对于力来说,情况也是如此:我们对 3D 线性力和力矩矢量使用了不同的符号,并在普吕克 坐标表中保留了它们的名称。
一般情况下,坐标的名称与矢量的名称相同。因此,如果 m^\hat{\boldsymbol{m}}m^ 和 f^\hat{\boldsymbol{f}}f^ 表示 M6\mathrm{\boldsymbol{M}}^6M6 和 F6\mathrm{\boldsymbol{F}}^6F6 的一般元素,分别,那么它们的普吕克坐标为
m^‾O=[mxmymzmOxmOymOz]=[m‾m‾O] and f^‾O=[fOxfOyfOzfxfyfz]=[f‾f‾O]
\underline{\hat{\boldsymbol{m}}}_O=\left[\begin{array}{c}
m_x \\
m_y \\
m_z \\
m_{O x} \\
m_{O y} \\
m_{O z}
\end{array}\right]=\left[\begin{array}{c}
\underline{\boldsymbol{m}} \\
\underline{\boldsymbol{m}}_O
\end{array}\right] \quad \text { and } \quad \underline{\hat{\boldsymbol{f}}}_O=\left[\begin{array}{c}
f_{O x} \\
f_{O y} \\
f_{O z} \\
f_x \\
f_y \\
f_z
\end{array}\right]=\left[\begin{array}{c}
\underline{\boldsymbol{f}} \\
\underline{\boldsymbol{f}}_O
\end{array}\right]
m^O=mxmymzmOxmOymOz=[mmO] and f^O=fOxfOyfOzfxfyfz=[ffO]
我们将始终按照先角度后直线的顺序列出普吕克坐标;也就是说,三个角度坐标将始终列在前面。不过,读者应该知道,先列出三个线性坐标也是完全可以接受的,也有文献使用这种排列方式。从数学角度来看,列出坐标的顺序并无区别。不过,从计算的角度来看 ,这确实很重要,因为软件通常是按照一种特定的顺序编写的。
2.5 线矢量和自由矢量(Line Vectors and Free Vectors)
如果空间中的一个矢量被约束在一条方向、位置固定的直线上,仅允许该矢量沿着直线前后移动,这个被直线约束的矢量被称为线矢量。 刚体的纯转动是线矢量,作用在刚体上的线性力也是线矢量。自由矢量是一个可以用大小和方向来表征的量。刚体的纯平移是自由矢量,纯耦合也是自由矢量。线矢量可以用五个数字表示,自由矢量可以用三个数字表示。线矢量也可以用自由矢量和直线上的任意一点来表示。
设 s^\hat{s}s^ 是任一空间向量、运动或力,设 sss 和 sOs_{O}sO 是两个 3D3 \mathrm{D}3D 坐标向量,它们提供了 s^\hat{\boldsymbol{s}}s^ 的普吕克坐标。以下是有关线矢量和自由矢量的一些基本定理。
- 如果 s=0\boldsymbol{s}=\mathbf{0}s=0 则 s^\hat{\boldsymbol{s}}s^ 是一个自由矢量。
- 如果 s⋅sO=0\boldsymbol{s} \cdot \boldsymbol{s}_{O}=0s⋅sO=0 则 s^\hat{\boldsymbol{s}}s^ 是一个线矢量。直线的方向由 s\boldsymbol{s}s 给出,线本身是满足 OP→×s=sO\overrightarrow{O P} \times \boldsymbol{s}=\boldsymbol{s}_{O}OP×s=sO 的点 PPP 的集合。
- 任何空间矢量都可以表示为线矢量和自由矢量之和。如果线向量必须穿过给定点,则表达式是唯一的。
- 除自由矢量外,任何空间矢量都可以唯一地表示为线性矢量与平行自 由矢量之和。运动矢量的表达式为
[ssO−hs]+[0hs] where h=s⋅sOs⋅s.(2.10) \left[\begin{array}{c} \boldsymbol{s} \\ \boldsymbol{s}_{O}-h \boldsymbol{s} \end{array}\right]+\left[\begin{array}{c} \mathbf{0} \\ h \boldsymbol{s} \end{array}\right] \quad \text { where } \quad h=\frac{\boldsymbol{s} \cdot \boldsymbol{s}_{O}}{\boldsymbol{s} \cdot \boldsymbol{s}} . \tag{2.10} [ssO−hs]+[0hs] where h=s⋅ss⋅sO.(2.10)
最后的结果意味着除了自由向量之外的任何空间向量都可以通过有向线、线性幅度和角度幅度唯一地描述。自由向量也可以用这种方式描述,但描述不是唯一的,因为只有线的方向很重要。根据螺旋理论,刚体最常见的运动包括绕空间中一条线的旋转以及沿该线的平移(即螺旋或螺旋运动)。这种运动称为扭转。同样,作用在刚体上的最常见的力由沿空间中的一条线作用的线性力以及围绕它作用的力偶组成(因此力和力偶是平行的)。这种力称为扳手。在这两种情况下,直线本身称为螺旋轴,自由矢量大小与直线矢量大小的比率称为螺距。纯自由矢量被视为无限螺距的扭曲和扳手,并且没有明确的螺旋轴。 M6和F6的元件可以分别被视为扭转件和扳手。
最后一个结论意味着,除了自由矢量之外,任何空间矢量都可以用一条有方向的直线、一个线性大小和一个角度大小来唯一描述。自由矢量也可以用这种方式描述,但这种描述并不是唯一的,因为只有直线的方向才是最重要的。 根据螺旋理论,刚体最常见的运动包括绕空间中的一条线的旋转以及沿该直线平移(即螺旋运动或拧转运动)。这种运动被称为扭转运动(twist)。同样,作用在刚体上的最常见的力由沿空间中的一条线作用的线性力以及围绕它作用的力偶组成(因此力和力偶是平行的)。这种力被称为wrench。在这两种情况下,线本身称为螺旋轴,自由矢量大小与线矢量大小之比称为螺距。 纯粹的自由矢量被视为无限间距的扭曲和扳手,并没有确定的螺旋轴。M6\mathrm{\boldsymbol{M}}^{6}M6 和 F6\mathrm{\boldsymbol{F}}^{6}F6 的元素可分别视为 twists 和 wrenches。
大小(Magnitude)
空间向量不是欧几里得向量,因此没有欧几里得意义上的幅值。但是,有四组空间矢量可以定义有意义的大小:旋转、平移、线性力和耦合(即 M6\mathrm{\boldsymbol{M}}^{6}M6 和 F6\mathrm{\boldsymbol{F}}^{6}F6 中的所有线向量和自由向量)。幅值只能在每组矢量中进 行比较;因此,例如一个旋转的幅值可以与另一个旋转的幅值进行比较 ,但不能与平移或力进行比较。
具有单位大小的矢量称为单位矢量。但是,“单位幅度”(‘unit magnitude’)的含义确实取决于所选的单位制。例如,单位旋转速度为每选定时间单位一个弧度 ,单位平移速度为每选定时间单位一个长度单位。因此,普吕克基矢量都是单位矢量,不仅取决于坐标系的位置和速度,还取决于所选的单位制。
2.6 标量积(Scalar Product)
标量积是在空间矢量上定义的,其中一个参数必须是运动矢量,另一个必须是力矢量,结果是表示能量、功率或某种类似量的标量。给定 m∈M6\boldsymbol{m} \in \mathrm{\boldsymbol{M}}^{6}m∈M6 和 f∈F6\boldsymbol{f} \in \mathrm{\boldsymbol{F}}^{6}f∈F6,标量积可以写成 m⋅f\boldsymbol{ m} \cdot \boldsymbol{f}m⋅f 或 f⋅m\boldsymbol{f} \cdot \boldsymbol{m}f⋅m,两者含义相同,但表达式 m⋅m\boldsymbol{m} \cdot \boldsymbol{m}m⋅m 和 $ \boldsymbol{f} \cdot \boldsymbol{f}$ 未定义(即 M6\mathrm{\boldsymbol{M}}^{6}M6 或 F6\mathrm{\boldsymbol{F}}^{6}F6 上没有内积) 。如果 f\boldsymbol{f}f 是作用在刚体上的力,m\boldsymbol{m}m 是该刚体的速度,则 m⋅f\boldsymbol{m} \cdot \boldsymbol{f}m⋅f 是由 f\boldsymbol{f}f 传递的功率。
标量积在 M6\mathrm{\boldsymbol{M}}^{6}M6 和 F6\mathrm{\boldsymbol{F}}^{6}F6 之间建立了联系,这种联系被正式称为对偶关系:每个空间都是另一个空间的对偶。这一性质对空间向量代数的实际影响 如下:
- 我们在 M6\mathrm{\boldsymbol{M}}^{6}M6 和 F6\mathrm{\boldsymbol{F}}^{6}F6 上使用对偶坐标;
- 力矢量和运动矢量遵循不同的坐标变换规则;
- 有两个叉积运算符:一个用于运动矢量,一个用于力矢量(参见 §2.9\S 2.9§2.9 )。
M6\mathrm{\boldsymbol{M}}^{6}M6 和 F6\mathrm{\boldsymbol{F}}^{6}F6 上的对偶坐标系是由两个底 {d1,…,d6}⊂M6\left\{\boldsymbol{d}_{1}, \ldots, \boldsymbol{d}_{6}\right\} \subset \mathrm{\boldsymbol{M}}^{6}{d1,…,d6}⊂M6 和 {e1,…,e6}⊂F6\left\{\boldsymbol{e}_{1}, \ldots, \boldsymbol{e}_{6}\right\} \subset \mathrm{\boldsymbol{F}}^{6}{e1,…,e6}⊂F6,其中基矢量满足条件
di⋅ej={1 if i=j0 otherwise. (2.11)
\boldsymbol{d}_{i} \cdot \boldsymbol{e}_{j}= \begin{cases}1 & \text { if } i=j \\ 0 & \text { otherwise. }\end{cases} \tag{2.11}
di⋅ej={10 if i=j otherwise. (2.11)
根据式2.2和2.7中 DO\mathcal{D}_{O}DO 和 EO\mathcal{E}_{O}EO 的定义。可以看出这些基底形成了一个对偶坐标系。(将 dOx\boldsymbol{d}_{O x}dOx 视为 d1,dOy\boldsymbol{d}_{1}, \boldsymbol{d}_{O y}d1,dOy 作为 d2\boldsymbol{d}_{2}d2,等等。对偶坐标系最重要的性质是,如果 m‾\underline{\boldsymbol{m}}m 和 f‾\underline{\boldsymbol{f}}f 表示 m∈M6\boldsymbol{m} \in \mathrm{\boldsymbol{M}}^{6}m∈M6 和 f∈F6\boldsymbol{f} \in \mathrm{\boldsymbol{F}}^{6}f∈F6 在对偶坐标系中的元素,则
m⋅f=m‾Tf‾.(2.12)
\boldsymbol{m} \cdot \boldsymbol{f}=\underline{\boldsymbol{m}}^{\mathrm{T}} \underline{\boldsymbol{f}} . \tag{2.12}
m⋅f=mTf.(2.12)
这一特性的直接结果是,我们需要为运动和力建立不同的坐标变换矩阵 。如果矩阵 X\boldsymbol{X}X 对运动矢量进行了坐标变换,而 X∗\boldsymbol{X}^{*}X∗ 对力矢量进行了相同的变换,则两者的关系为
X∗=X−T(2.13)
\boldsymbol{X}^{*}=\boldsymbol{X}^{-\mathrm{T}} \tag{2.13}
X∗=X−T(2.13)
这个公式由这个条件推导出: m‾Tf‾=(Xm‾)T(X∗f‾)\underline{\boldsymbol{m}}^{\mathrm{T}} \underline{\boldsymbol{f}}=(\boldsymbol{X} \underline{\boldsymbol{m}})^{\mathrm{T}}\left(\boldsymbol{X}^{*} \underline{\boldsymbol{f}}\right)mTf=(Xm)T(X∗f) 对于所有 m‾\underline{\boldsymbol{m}}m 和 f‾\underline{\boldsymbol{f}}f 成立。
2.7 使用空间矢量(Using Spatial Vectors)
空间矢量是表达和分析刚体和刚体系统动力学的工具。本节列出了空间矢量的使用规则,描述了空间矢量与其表示的物理现象之间的联系。最后几个条目预览了一些我们尚未遇到的量的规则:加速度、动量和惯性。这个列表并不完整。
用法:M6\mathrm{\boldsymbol{M}}^{6}M6 的元素描述刚体运动的各个方面,例如:速度、加速度、无穷小位移以及运动自由度和约束的方向。 F6\mathrm{\boldsymbol{F}}^{6}F6 的元素描述作用在刚体上的力,以及与力相关的量,例如:动量、冲量以及力自由度和约束的方向。
唯一性:M6\mathrm{\boldsymbol{M}}^{6}M6 的元素与刚体所有可能运动的集合之间存在 1:1 映射。同样,F6\mathrm{\boldsymbol{F}}^{6}F6 的元素与作用在刚体上的所有可能力的集合(即所有wrenches的集合)之间存在 1:11: 11:1 映射。
相对速度:如果刚体 B1B_{1}B1 和 B2B_{2}B2 的速度分别为 v1\boldsymbol{v}_{1}v1 和 v2\boldsymbol{v}_{2}v2,则B2B_{2}B2 相对于 B1B_{1}B1 的相对速度为 vrel=v2−v1\boldsymbol{v}_{r e l}=\boldsymbol{v}_{2}-\boldsymbol{v}_{1}vrel=v2−v1。
刚性连接:如果两个物体刚性连接在一起,则它们的速度相同。
力的总和:如果力 f1\boldsymbol{f}_{1}f1 和 f2\boldsymbol{f}_{2}f2 都作用在同一刚体上,则它们相当于单个力 ftot \boldsymbol{ f}_{\text {tot }}ftot ,由 ftot =f1f2\boldsymbol{f}_{\text {tot }}=\boldsymbol{f}_{1} \boldsymbol{f}_{2}ftot =f1f2 给出。
作用力和反作用力:如果刚体 B1B_{1}B1 对刚体 B2B_{2}B2 施加 f\boldsymbol{f}f 的力,则 B2B_{2}B2 对B1B_{1}B1 产生−f-\boldsymbol{f}−f 的力(牛顿第三定律)。
标量积:如果力 f\boldsymbol{f}f 作用在速度为 v\boldsymbol{v}v 的刚体上,则该力传递的功率为 f⋅v\boldsymbol{f} \cdot \boldsymbol{v}f⋅v。
缩放:作用在速度为 βv\beta \boldsymbol{v}βv 的刚体上的 αf\alpha \boldsymbol{f}αf 的力,所产生的功率是是作用在速度为 v\boldsymbol{v}v 的物体上的 f\boldsymbol{f}f 力所产生的能量的 αβαβαβ 倍。以 v\boldsymbol{v}v 等速运动的刚体在 α\alphaα 个单位时间内进行的运动与以 αv\alpha \boldsymbol{v}αv 速度运动的刚体在一个单位时间内进行的运动相同。
加速度:空间加速度是空间速度的变化率。空间加速度是真正的矢量,并遵循与速度相同的求和规则。例如,如果 vrel=v2−v1\boldsymbol{v}_{r e l}=\boldsymbol{v}_{2}-\boldsymbol{v}_{1}vrel=v2−v1 则 arel=a2−a1\boldsymbol{a}_{r e l}=\boldsymbol{ a}_{2}-\boldsymbol{a}_{1}arel=a2−a1。
惯性之和:如果刚体 B1B_{1}B1 和 B2B_{2}B2 的惯性分别为 I1\boldsymbol{I}_{1}I1 和 I2\boldsymbol{I}_{2}I2,并且它们是相连的在一起形成单个复合刚体,则复合体的惯性为 I1+I2\boldsymbol{I}_{1} + \boldsymbol{I}_{2}I1+I2。
动量:如果刚体的空间惯性为 I\boldsymbol{I}I,速度为 v\boldsymbol{v}v,则其动量为 Iv\boldsymbol{I} \boldsymbol{v}Iv。
运动方程:刚体动量的变化率等于作用在其上的力;即f=d/dt(Iv)\boldsymbol{f}=\mathrm{d} / \mathrm{d} t(\boldsymbol{I} \boldsymbol{v})f=d/dt(Iv)。如果我们进行微分,则得到公式 f=Iav×∗Iv\boldsymbol{f}=\boldsymbol{I} \boldsymbol{a} \boldsymbol{v} \times^{*} \boldsymbol{I} \boldsymbol{v}f=Iav×∗Iv 。
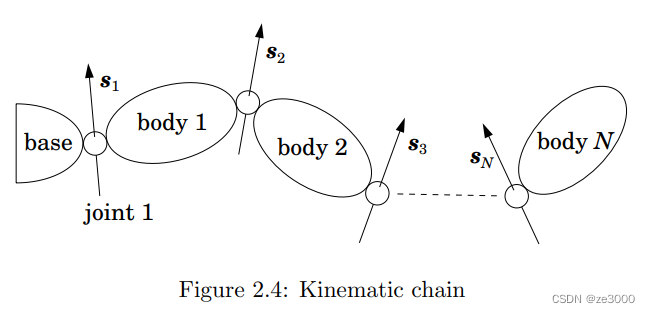
示例 2.3 图 2.4 显示了一个由多个刚体组成的运动链,一端连接到固定基座。这样的系统是典型的工业机械臂,称为运动链。该系统中共有NNN个运动刚体和NNN个关节,这些刚体连接在一起,使得关节 iii 从体 i−1i-1i−1 连接到体iii。 (基座为刚体 0。)我们说关节连接着 “从” 一个刚体 "到 " 另一个刚体,这样我们就可以将穿过关节的速度定义为 “到” 刚体相对于 "从"刚体的速度。因此,如果 vJi\boldsymbol{v}_{J i}vJi 是跨关节 iii 的速度,而 vi\boldsymbol{v}_{i}vi 是刚体 iii 的速度,那么
vJi=vi−vi−1.(2.14)
\boldsymbol{v}_{J i}=\boldsymbol{v}_{i}-\boldsymbol{v}_{i-1} . \tag{2.14}
vJi=vi−vi−1.(2.14)
我们假设每个关节只有一个自由度,因此 vJi\boldsymbol{v}_{J i}vJi 可以被描述为单个运动矢量的标量倍数。即
vJi=siq˙i(2.15)
\boldsymbol{v}_{\mathrm{J} i}=\boldsymbol{s}_{i} \dot{q}_{i} \tag{2.15}
vJi=siq˙i(2.15)
其中 si\boldsymbol{s}_{i}si 和 q˙i\dot{q}_{i}q˙i 是关节 iii 的轴矢量和速度变量。如果关节 iii 是 旋转关节,则 si\boldsymbol{s}_{i}si 将是一个单位旋转矢量,因此 vJi\boldsymbol{v}_{\mathrm{J} i}vJi 在 q˙i=1\dot{q}_{i}=1q˙i=1 时将是单位旋转速度。同样,如果关节 iii 是平移关节,则 si\boldsymbol{s}_{i}si 将是一个单位平移矢量。
让我们计算出系统中每个刚体的速度。从等式 2.14 和 2.15 我们有
vi=vi−1+siq˙i.(v0=0)(2.16)
\boldsymbol{v}_{i}=\boldsymbol{v}_{i-1}+\boldsymbol{s}_{i} \dot{q}_{i} . \quad\left(\boldsymbol{v}_{0}=\mathbf{0}\right) \tag{2.16}
vi=vi−1+siq˙i.(v0=0)(2.16)
通过这个等式,我们可以依次计算出每个刚体的速度,从基座开始,一直计算到运动链的自由端。速度的另一个表达式是
vi=∑j=1isjq˙j \boldsymbol{v}_{i}=\sum_{j=1}^{i} \boldsymbol{s}_{j} \dot{q}_{j} vi=j=1∑isjq˙j
从计算角度来看,公式 2.16 比公式 2.17 更有效率,因为它重复使用了 之前的计算结果。vi\boldsymbol{v}_{i}vi 的另一个表达式是
vi=[s1s2⋯si0⋯0][q˙1⋮q˙N]=Jiq˙.
\boldsymbol{v}_{i}=\left[\begin{array}{lllllll}
\boldsymbol{s}_{1} & \boldsymbol{s}_{2} & \cdots & \boldsymbol{s}_{i} & \mathbf{0} & \cdots & \mathbf{0}
\end{array}\right]\left[\begin{array}{c}
\dot{q}_{1} \\
\vdots \\
\dot{q}_{N}
\end{array}\right]=\boldsymbol{J}_{i} \dot{\boldsymbol{q}} .
vi=[s1s2⋯si0⋯0]q˙1⋮q˙N=Jiq˙.
在这个公式里, Ji\boldsymbol{J}_{i}Ji 是一个 6×N6 \times N6×N 的矩阵,称为第 iii 个刚体的雅可比矩阵, 且 q˙\dot{\boldsymbol{q}}q˙ 关节空间速度矢量。





















 1117
1117

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








