Sequential Logic-Latchs and Flip-Flops

原创

已于 2022-02-12 15:04:52 修改 · 349 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#fpga开发

于 2022-01-25 14:26:09 首次发布

本文详细介绍了数字系统设计中的各种触发器实现方法，包括基本的D触发器、带同步复位的D触发器、16位D触发器、锁存器、JK触发器以及脉冲边沿检测等高级应用。同时探讨了这些触发器如何用于信号检测和状态维护。

D触发器：

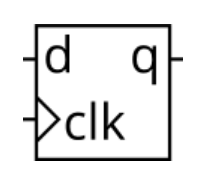
module top_module (
    input clk,    // Clocks are used in sequential circuits
    input d,
    output reg q );//
    always @(posedge clk) begin
         q<=d;
    end
    // Use a clocked always block
    //   copy d to q at every positive edge of clk
    //   Clocked always blocks should use non-blocking assignments

endmodule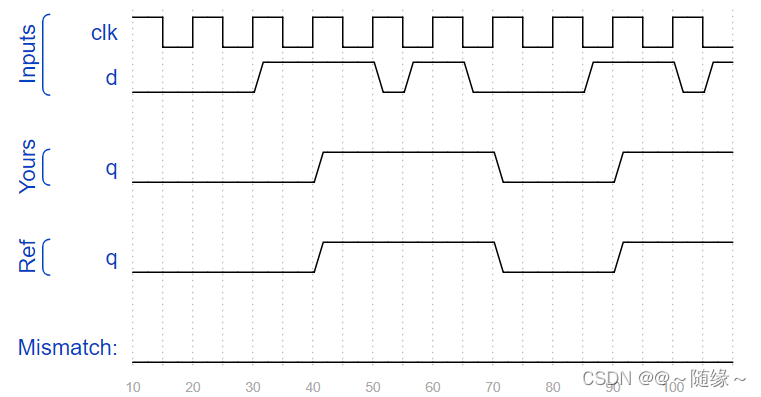

加reset：

Create 8 D flip-flops with active high synchronous reset. All DFFs should be triggered by the positive edge of clk.

module top_module (
    input clk,
    input reset,            // Synchronous reset
    input [7:0] d,
    output [7:0] q
);
    always @(posedge clk) begin
        if(!reset)
            q<=d;
        else
            q<=1'b0;
    end
endmodule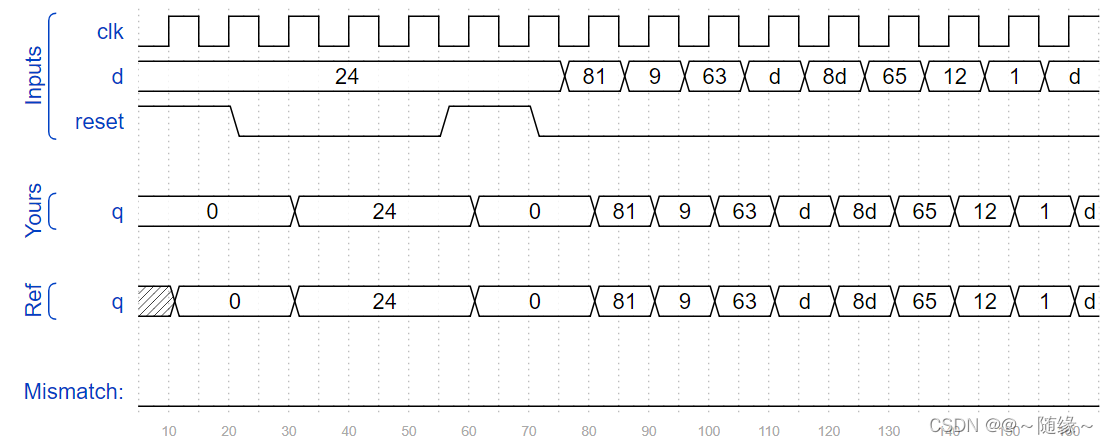

创建一个16D触发器，有时我们仅需要修改部分触发器中的值。字节使能信号控制当前时钟周期中16个寄存器中哪个字节需被修改。byteena[1]控制高字节d[15:8]，而byteena[0]控制低字节d[7:0]。

resetn是一个同步，低复位信号。

所有的D触发器由时钟的上升沿触发。

module top_module (
    input clk,
    input resetn,
    input [1:0] byteena,
    input [15:0] d,
    output [15:0] q
);

    always @(posedge clk) begin
        if(resetn) begin
            if(byteena[1])