斐波那契数列的三种解法

斐波那契数列是面试过程中很基础的问题，数列的定义如下所示，每个数字都可以拆解成之前两个数的和，直至拆解到0和1的组合。这种递归拆解的问题，如果拆解算法取用的方式不同，计算量和计算速度有着天壤之别。

1.采用树形递归进行求解

采用树形递归方法，作为典型的树形递归具有教育意义，但是却是一种很糟糕的计算方式，因为做了太多的冗余计算。

 

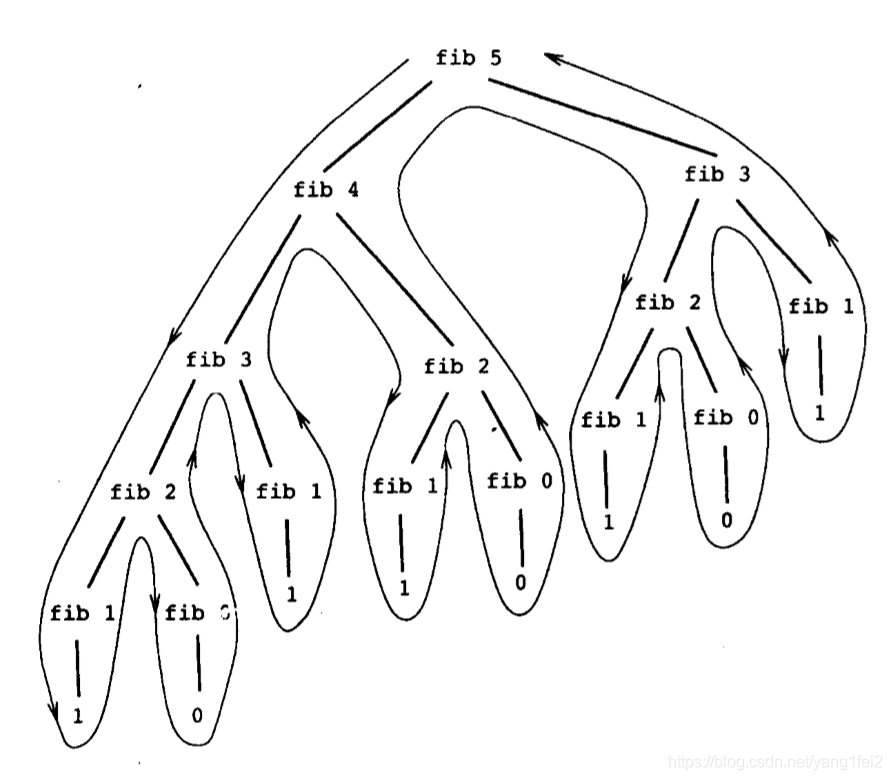
可以证明Fib(n)值的增长相对于n是指数关系，该过程所用的计算步骤数将随着输入增长而指数性的增长，另一方面其空间需求随着输入增长而线性增长，因为, 在计算中的每一点，我们都只需保存树中在此之上的结点的轨迹。一般说，树形递归计算过程里所需的步骤数将正比于树中的结点数，其空间需 求正比于树的最大深度。

 

2.Fib(n)就是最接近某个表达式的整数

该表达式如下所示:

 

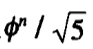
其中∅就是黄金分割比，满足如下表达式

 

 

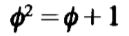
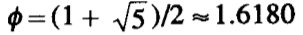
这是一个经验总结，至于如何推导也没搞明白，但确是正确的

3.以线性迭代的方式计算斐波那契数列

(define (fib n)
    (fib-itor 1 0 n))
(define (fib-iter a b count)
    (if (= count 0)
        b
        (fib-iter (+ a b) a (- count 1))))    

计算Fib(n)这种方法是一个线性迭代，和树状展开相比这两种方法在计算所需的步骤上有很大的差异巨大，后一个方法相对于n为线性的，前一个相对于n是指数的。虽然第一个fib过程远比第二个低效，但它却更加直截了当，基本上就是将斐波那契序列的定义直接翻译为Lisp语言。

下面通过C++语言实现三种计算斐波那契数列的方法，供大家参考，大家可以比较一下计算效率。

#include <iostream>
long long fib(int n)
{
	if (n == 0)
	{
		return 0;
	}
	if (n == 1)
	{
		return 1;
	}
	return fib(n - 1) + fib(n-2);
}
long long fib_split(int n)
{
	double splitValue = (1.0 + sqrt(5)) / 2.0;
	return round(pow(splitValue,n) / (double)sqrt(5));
}

long long fib_thread_sub(int a, int b, int count)
{
	if (count == 0)
	{
		return b;
	}
	return fib_thread_sub(a + b, a, count - 1);
}

long long fib_thread(int n)
{
	return fib_thread_sub(1, 0, n);
}
int main()
{
	for (int index = 0; index < 20; ++index)
	{
		std::cout << fib(index) << ":" << fib_split(index) << ":" << fib_thread(index) << std::endl;
	}

}

没有对比就没有伤害，当n的值足够大的时候，三种解法的计算速度有着天壤之别，所以说在解决特定的问题的时候换个思路可能会有意想不到的效果。