[学习笔记]省选算法·点分治&动态点分治

一、开头

（四川省神犇协会）
神犇 1 号：所有神犇集合！我们协会里要开一场关于 D xyz32768 的会议。
（会议）
神犇 1 号：大家决定用什么算法去 D xyz32768 呢？
神犇 16 号：当然是用协会里没有一个人不会，但 xyz32768 不会的点分治了！
神犇 1 号：Good job!就这样！
（X省Y市）
xyz32768：你们是哪省神犇协会派来的人啊？
神犇 11111 号：当然是 SC 了！我们派来了 $10^5$ 个人专门来考察你会不会点分治这种 sb 算法。
xyz32768：淀粉质是个什么算法？难不成是 (C6H10O5)n ？
神犇 15 号 & 神犇 174 号：哈哈，菜啊！既然你不知道什么叫点分治，就来问你：一个 $n$ 个点的树，树有边权，求有多少对点 $(u,v)$ 满足 $u$ 到 $v$ 的距离小于等于一个给定的整数 $k$ ？
xyz32768：仿佛只会 $O(n^2\log n)$ 啊。
神犇 3377 号：你必须在 $10^{-13}$ 秒内想出一个 $O(n\log^2n)$ 的算法，否则我们会对全世界说 xyz32768 最菜！
xyz32768：啥？ $O(n\log^2n)$ ？
神犇 1010 号（大声唱）：千年 D 一回， D 一会啊！千年 D 一回， xyz32768 好菜啊！是谁在耳边说：xyz32768 好垃圾……

二、引言

开头中 SC 神犇 15 号 & 174 号提出的问题就是点分治的一个经典模型：
一个 $n$ 个节点的树，求树上有多少对点 $(u,v)$ 满足 $u$ 到 $v$ 的距离小于等于 $k$ 。
点分治是树分治中的一种。树分治可用来解决关于树上路径的问题。

三、点分治

点分治的基本思想是：
找到树的重心（分出的子树最小的节点） $x$ （可以证明 $x$ 分出的子树大小不大于整棵树的一半），然后处理好经过点 $x$ 的路径，再往每个子树递归下去。
即要处理三种情况：
（1） $u$ 和 $v$ 属于同一子树：

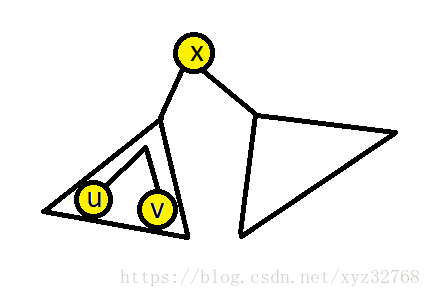
（2） $u$ 和 $v$ 属于不同子树：

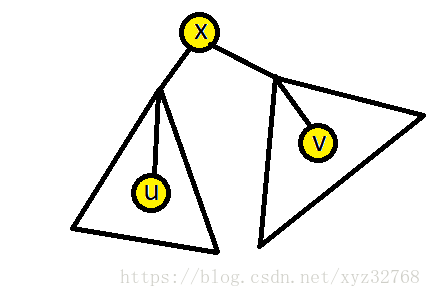
（3）路径的一个端点为 $x$ ：

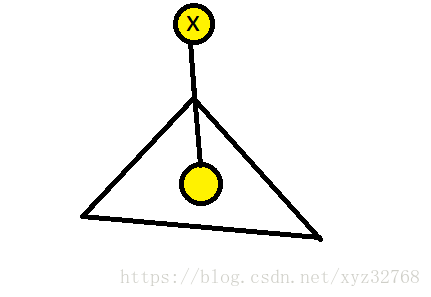
情况（1）可以往子树递归处理。情况（2）（3）则是过点 $x$ 的路径。
下面就 SC 神犇提出的问题进行讨论：
求出 $x$ 的子树内所有点 $u$ 到 $x$ 的距离 $d_u$ 。那么一条路径 $(u,v)$ （ $u$ 和 $v$ 不在同一子树内）就可以表示成 $d_u+d_v$ 的形式。
然后可以发现（2）（3）实际上是同一种情况，都可以表示成 $d_u+d_v$ 的形式。
先不考虑 $u$ 和 $v$ 是否在同一子树内。
这时候就是求 $x$ 的子树内有多少对 $u,v$ 满足 $d_u+d_v\leq k$ 。
将 $d$ 值排序之后，使用两个指针扫描 $d$ ，就可以得出一个 $O(结点个数)$ 的算法。
当然，这时候还需要去除 $u$ 和 $v$ 来自同一子树带来的影响。也就是说，这时候要枚举 $x$ 的子节点 $w$ ，然后把答案减去 $w$ 的子树内满足 $d_u+d_v\leq k$ 的点对数。
由于每一次都进行了排序，每递归一次子问题规模至少降低一半，
所以复杂度 $O(n\log^2n)$ 。
树分治的过程就是：
1、找重心→2、处理过重心的路径→3、往子树递归。

四、模板

找重心：

void dfs1(int u, int fu) { // 计算每个点的 size
    maxs[u] = 0; sze[u] = 1; Edge(u) {
        if ((v = go[e]) == fu || vis[v]) continue;
        dfs1(v, u); sze[u] += sze[v]; maxs[u] = max(maxs[u], sze[v]);
    }
}
void dfs2(int r, int u, int fu) {
    maxs[u] = max(maxs[u], sze[r] - sze[u]);
    // maxs[u] 为 u 分出的最大子树的大小
    if (maxs[u] < maxs[G]) G = u; Edge(u) {
        if ((v = go[e]) == fu || vis[v]) continue;
        dfs2(r, v, u);
    }
}
void calcG(int u) {dfs1(u, 0); G = u; dfs2(u, u, 0);} // 找重心

点分治：

void solve(int u) {
    calcG(u); deal(G); // 处理 G 的子树内过重心的路径
    vis[G] = 1; // 找到重心后将重心标记，避免重复经过
    Edge(G) if (!vis[v = go[e]]) solve(v); // 往子树递归
}

五、动态点分治

有时候我们的目的不仅仅是在树上进行统计，还要在分治结束之后对树进行一些询问，甚至修改，如 BZOJ 1095 / ZJOI 2007 捉迷藏。这时候就需要扩展到动态点分治。动态点分治，实际上和点分治比较相似：

void dfs3(int u, int fu) {
    calcG(u); deal(G); vis[G] = 1; fa[G] = fu; int t = G;
    Edge(G) if (!vis[v = go[e]]) dfs3(v, t);
}

注意到多了一句：

fa[G] = fu;

也就是建立了一棵分治树，在分治的过程中，如果某一次以 $x$ 为重心进行分治， $x$ 有一个子树的重心为 $y$ ，就把 $x$ 作为 $y$ 在分治树上的父亲。也就是说，动态点分治就是在分治的过程中，对于每个分治重心 $x$ ，从 $x$ 向 $x$ 的所有子树的重心连了一条边，形成了一棵分治树。
这样就能对树进行查询，甚至修改操作了。
图解大概这样（虚线表示分治树上的边，父亲指向儿子）：

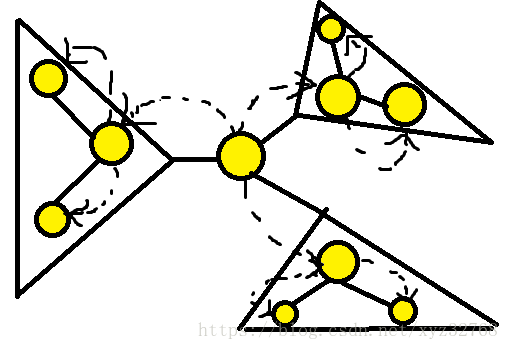
六、动态点分治之加点操作

这一部分还是要从 WC 2014 紫荆花之恋说起。由于此题不是简单地修改，而是每次动态地添加一个叶子节点。这时候如果要加点 $y$ 并将 $x$ 作为 $y$ 的父亲，那么看上去只需要在分治树上将 $x$ 作为 $y$ 的父亲即可，但这样会遇到复杂度的问题：这样建出的分治树是不平衡的。因此还需要利用替罪羊树的思想，在分治树上加边 $(x,y)$ 后，要在 $x$ 的祖先里找到一个深度最小的，不满足平衡性质的点 $u$ ，然后暴力重构 $u$ 的子树。利用势能分析可以得出复杂度为均摊 $O(\log^2n)$ 。

七、题目

点分治：
1、[BZOJ1758][Wc2010]重建计划：
https://www.lydsy.com/JudgeOnline/problem.php?id=1758
2、[BZOJ2599][IOI2011]Race：
https://www.lydsy.com/JudgeOnline/problem.php?id=2599
3、[BZOJ4598][Sdoi2016]模式字符串：
https://www.lydsy.com/JudgeOnline/problem.php?id=4598
动态点分治：
1、[BZOJ1095][ZJOI2007]Hide 捉迷藏：
https://www.lydsy.com/JudgeOnline/problem.php?id=1095
2、[BZOJ3924][Zjoi2015]幻想乡战略游戏：
https://www.lydsy.com/JudgeOnline/problem.php?id=3924
3、[BZOJ4012][HNOI2015]开店：
https://www.lydsy.com/JudgeOnline/problem.php?id=4012
4、[BZOJ3435][UOJ55][Wc2014]紫荆花之恋：
https://www.lydsy.com/JudgeOnline/problem.php?id=3435
http://uoj.ac/problem/55