动态点分治详解

动态点分治大意：利用没有树结构修改的性质预处理重心树优化时间

其实就是很暴力的思想，因为树的结构不变，所以每一次找到的重心都一样，可以用一次点分树预处理一下点分治的重心，再连接相邻的重心便是点分树。

---

前置知识：点分治

见另一篇blog：

---

算法：

好像就没什么了，上面就是全过程
详细一点的分析：

1. 找到当前子树重心x
2. 深搜x的每一个儿子的子树，找到每一棵子树的重心y（两个重心的话随便取一个）
3. 对每一个y重复操作1和2
   

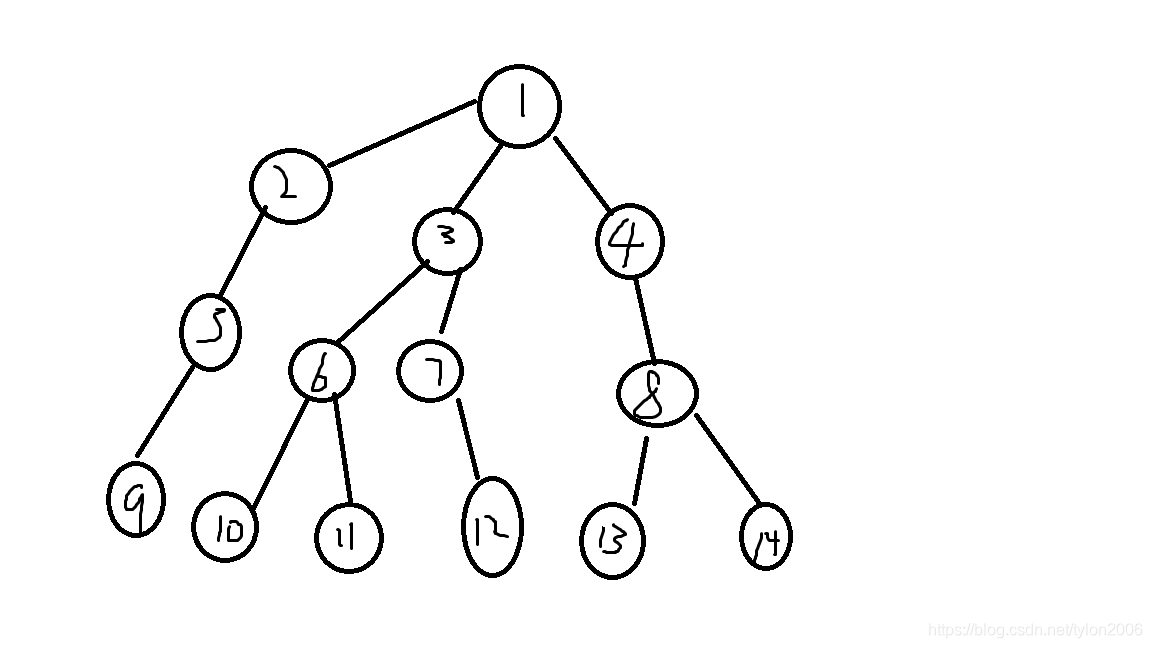
这里有一棵丑陋的树，我们模拟一下建点分树的过程，"-"表示深搜和连边：

• (1)
• (1->3,5,8)
• (5->2,9) (3->6,7) (8->4,13,14)
• (2) (4) (6->10,11) (7->12) (9) (13) (14)
• (10) (11) (12)

建出来长这样：

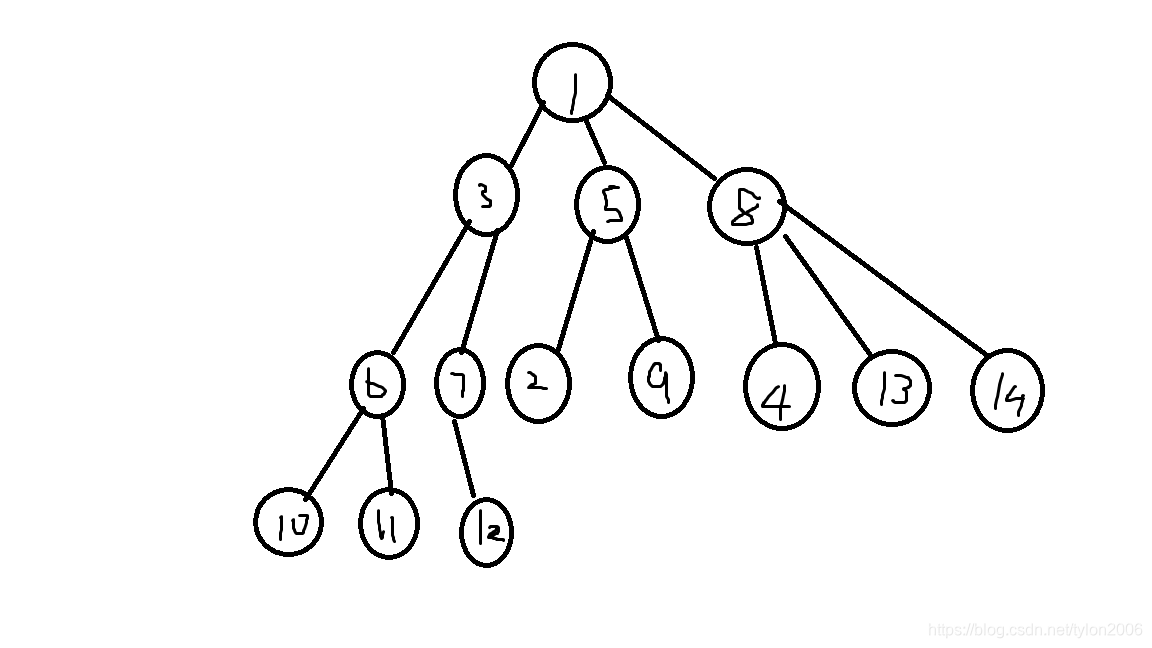
这个东西明显有两个性质：

1. 点分树上的子树必然包括原树上的子树（请读者自行思考）
2. 点分树的树高最大为$\log n$（证明如下，其实也应该自己思考）
   重心的每一棵子树的大小都小于原树的二分之一
   那么每次至少都会把原树劈成两半
   我们最多需要$\log n$次把树劈没
   即树高最大为$\log n$，而且严重跑不满（完全二叉警告

一般来说是不需要真的建出来的，拿一个fa记一下父亲上跳就行，原因见下文。

对于大部分题都是求路径，操作为查询和单点修改，根据点分治的性质，每次修改x只会影响到点分树上根到x的点的权值，所以从下往上跳就行了。

这种问题一般不包括修改树结构的操作，因为一改全树重心都会改变，属于LCT问题，求大佬踩
对于有修改的题一般是在上一次答案的基础上修改

---

模板：

#include<bits/stdc++.h>
using namespace std;
int e[1000010],nxt[1000010],head[100010],cnt;
int fa[100010],dis[100010],siz[100010];
bool vis[100010]；
int n,q,maxn=2e9,ss,len