1.列空间
2.零空间
1.列空间
1).列空间简介
设A是一个m * n的矩阵, 其列向量为a1, a2, ... an, 其中ai ∈ R^n
a.矩阵A的列空间, 记作Col(A)或C(A), 定义如下:
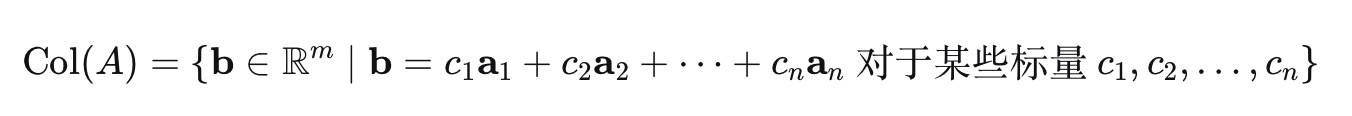
b.换句话说, Col(A)是矩阵A"线性无关的列向量"线性组合形成的集合, 它是R^m的一个子空
间; 因此,
Col(A) = Span {a1, a2.. an}, 矩阵A的列向量张成的空间
2).列空间与线性方程组的联系
列空间最直接, 最重要的应用在于理解线性方程组Ax = b的解的情况, 考虑方程组: Ax = b
其中A是m * n矩阵, x是n维未知向量, b是m维常数向量; 根据矩阵乘法的列视角, 这个方程可
以写成:
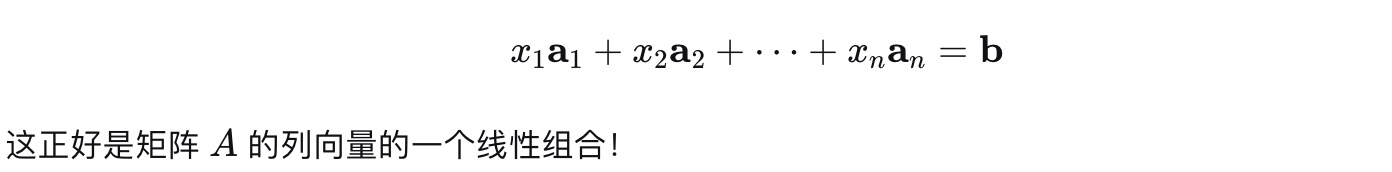
我们可以得出一个重要的结论:
"线性方程组Ax = b存在解, 当前仅当向量b在矩阵A的列空间中"

2.零空间
零空间就是"方程Ax = 0的所有解的集合"

1).Ax = 0的实例



2).判断方程组解的唯一性
对于方程Ax = b, 如果A的零空间只有零向量, 那么当Ax = b有解时, 也是唯一的


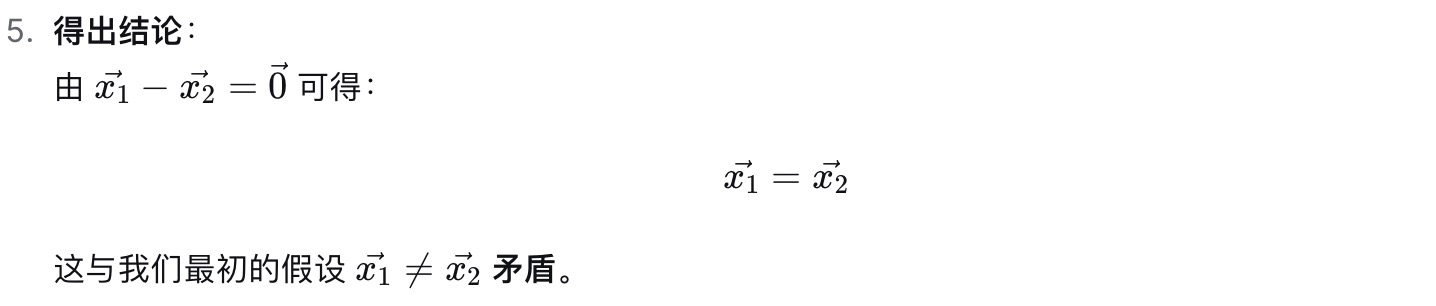






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








