【LeetCode热题100道笔记】杨辉三角

题目描述

给定一个非负整数 numRows，生成「杨辉三角」的前 numRows 行。

在「杨辉三角」中，每个数是它左上方和右上方的数的和。

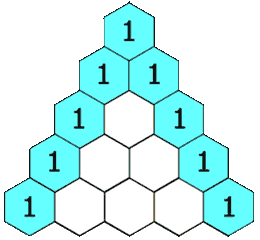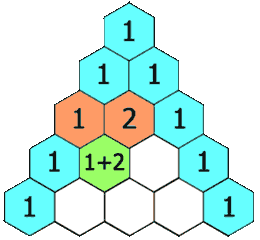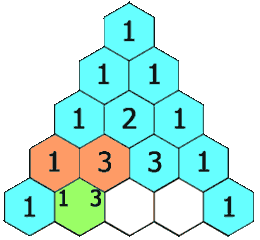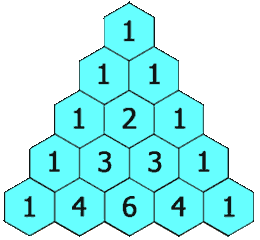
示例 1:
输入: numRows = 5
输出: [[1],[1,1],[1,2,1],[1,3,3,1],[1,4,6,4,1]]

示例 2:
输入: numRows = 1
输出: [[1]]

提示:

• 1 <= numRows <= 30

思考

基于杨辉三角的数学性质，采用逐行模拟构建的思路：

1. 杨辉三角的核心规律：
   • 每行的首尾元素均为 1；
   • 每行中间的第 j 个元素（1 < j < 行长度-1），等于上一行第 j-1 个元素与第 j 个元素之和。
2. 算法逻辑：用二维数组存储结果，先初始化第 1 行（固定为 [1]），再从第 2 行开始，根据上一行的元素逐行生成当前行，直至生成 numRows 行。

算法过程

1. 初始化结果：创建二维数组 result，存入第 1 行 [1]（杨辉三角第 1 行固定为 1）。
2. 逐行生成（从第 2 行到第 numRows 行）：
   • 设当前生成第 i 行（i 从 2 到 numRows），该行长度为 i，先初始化数组 row，并将首尾元素 row[0] 和 row[i-1] 设为 1；
   • 计算中间元素（j 从 1 到 i-2）：row[j] = result[i-2][j-1] + result[i-2][j]（result[i-2] 对应上一行，因数组索引从 0 开始）；
   • 将生成的 row 加入 result。
3. 返回结果：result 即为 numRows 行的杨辉三角。

时空复杂度

• 时间复杂度：O(numRows²)，共生成 numRows 行，第 i 行需计算 i-2 个中间元素，总操作数为 1+2+...+(numRows-1) = numRows×(numRows-1)/2，属于 O(numRows²)。
• 空间复杂度：O(numRows²)，需用二维数组存储所有行的元素（无额外冗余空间）。

代码

/**
 * @param {number} numRows
 * @return {number[][]}
 */
var generate = function(numRows) {
    const result = [[1]];
    for (let i = 2; i <= numRows; i++) {
        const row = Array(i);
        row[0] = 1;
        row[i-1] = 1;
        for (let j = 1; j < i-1; j++) {
            row[j] = result[i-2][j-1] + result[i-2][j];
        }
        result.push(row);
    }

    return result;
};