【OD机试题解法笔记】矩阵匹配

原创已于 2025-11-24 18:01:52 修改 · 1.4k 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2025-06-09 14:05:55 首次发布

OD机试题笔记专栏收录该内容

70 篇文章

订阅专栏

题目

从一个 N * M（N ≤ M）的矩阵中选出 N 个数，任意两个数字不能在同一行或同一列，求选出来的 N 个数中第 K 大的数字的最小值是多少。

输入描述
输入矩阵要求：1 ≤ K ≤ N ≤ M ≤ 150

输入格式
N M K
N*M矩阵

输出描述
N*M 的矩阵中可以选出 M! / (M-N)! 种组合数组，每个组合数组中第 K 大的数中的最小值。无需考虑重复数字，直接取字典排序结果即可。

备注
注意：结果是第 K 大的数字的最小值

用例

输入	输出	说明
3 4 2 1 5 6 6 8 3 4 3 6 8 6 3	3	N*M的矩阵中可以选出 M！/ (M - N)！种组合数组，每个组合数组种第 K 大的数中的最小值；上述输入中选出数组组合为： 1,3,6; 1,3,3; 1,4,8; 1,4,3; ...... 上述输入样例中选出的组合数组有24种，最小数组为1,3,3，则第2大的最小值为3

输入

输出

说明

3 4 2

1 5 6 6

8 3 4 3

6 8 6 3

N*M的矩阵中可以选出 M！/ (M - N)！种组合数组，每个组合数组种第 K 大的数中的最小值；

上述输入中选出数组组合为：

1,3,6;

1,3,3;

1,4,8;

1,4,3;

......

上述输入样例中选出的组合数组有24种，最小数组为1,3,3，则第2大的最小值为3

思考一（暴力解法）

N*M 的矩阵中可以选出 M！/ (M - N)！种组合数组是怎么计算的？题目要求从 N 行 M 列（N≤M）的矩阵中选 N 个数，满足 “任意两个数字不在同一行或同一列”。这种选法的本质是：

每行必须选 1 个数（因为共 N 行，要选 N 个数，每行恰好 1 个）；
列不能重复（每个数的列索引必须唯一）。

因此，选法的核心是为每一行分配一个唯一的列索引，即从 M 列中 “有序地选择 N 列”（因为不同行对应不同列的顺序不同，算不同的选法）。

排列数计算：

从 M 列中选 N 列并 “有序排列”（对应 N 行的顺序），这是排列问题，计算公式为：
P(M, N) = M × (M-1) × (M-2) × ... × (M - N + 1) = M! / (M - N)!

例如：当 N=3，M=4 时，选法总数为 4×3×2 = 24，即 4! / (4-3)! = 24 / 1 = 24，与实际计算一致

暴力解法就是根据约束条件枚举这么多组合计算每个组合的第 K 小的数字再更新全局第 K 小的数字。由于所有数字不能同行同列，不能像 DFS 搜索矩阵那样上下左右递归搜索。但是思路应该是相似的，难点在于没有限制只能访问当前位置的相邻元素，可以是不相邻的，而且必须是和当前搜索路径中已经搜索的所有数字不同行同列。以当前位置搜索下一个元素就不是从当前位置周边展开搜索了，这样代码也不好写，试想我可以搜索周围四个角的位置元素，它们和当前位置不同行不同列，但是未必和之前搜索过的数字也不同行不同列，那么正确的做法是不是从头开始遍历整个矩阵，排除和已经访问过数字同行或同列的数字，其余就是可以访问的数字。可以定义行哈希集合和列哈希集合存储每条路径访问过的数字位置行列索引，这样下次访问别的数字就可以进行位置一一比对筛选不同行不同列数字，回溯的时候再移除最新加入的元素。每次怎么记录第 K 小的数字，每次路径搜索结束时访问的数字序列长度达到 N 时就对序列降序排序取第 K 个元素，用快速排序需要O(N log(N))复杂度，感觉有些浪费，可以用优先队列维护 K 个元素，堆顶记录第 K 大（小）元素，复杂度是O(log n)要比排序更好。回溯时要从优先队列移除之前添加的元素，优先队列每次添加元素会发生堆调整，比较麻烦，需要记录添加的元素位置，以便回溯的时候删除。

基本思路：

枚举矩阵中每个数字作为起点进行搜索，定义一个count作为dfs函数参数记录访问的数字数量，到K时终止一次搜索路径。定义rowSet和colSet存放行列索引，每次搜索时查询set筛选不同行不同列数字；
选择下一个不同行不同列且未访问过的数字进行搜索，利用备忘录 visited 记录访问过的位置避免下次回溯又重复访问，维护一个优先队列（最小堆）存放 K 个数字；
当搜索序列长度达到 N 时从优先队列中取出堆顶的数字即局部第K大的数字更新全局所有第K大的数字中的最小值。

最小堆的作用：动态维护前 K 大元素

最小堆的堆顶是堆中最小的元素。
当需要维护当前最大的 K 个元素时，最小堆可以保证：
- 堆中始终保存当前已知的最大 K 个元素。
- 堆顶是这 K 个元素中的最小值（即第 K 大元素）。

时间复杂度很高 O(M!/(M-N)!)，只能处理很小的数据量，没有实际价值。

思考二（二分查找+二分图最大匹配数)

暴力解法（DFS + 最小堆）在理论上可以解决问题，但无法满足题目给定的规模输入（N≤M≤150）。查阅资料得知可以用二分查找 + 增广路径算法解决。在一个矩阵中选取 N 个元素，要求这些元素位于不同的行和列。可以将行号和列号分别看作二分图的两个部分，寻找 N 个互不同行同列的元素，就相当于在这个二分图中找到 N 条边的匹配。理解这个问题需要先明白什么是二分图？

我记忆中根据染色来判断一个图是不是二分图，能使用两种颜色对所有图节点染色且使所有相邻节点颜色不同，这样的图就是二分图。更严谨地说，二分图是一种特殊的图结构，其顶点可以被分为两个不相交的集合（通常称为 “左部” 和 “右部”），且图中所有的边都只连接左部集合和右部集合中的节点，同一集合内的节点之间没有边。

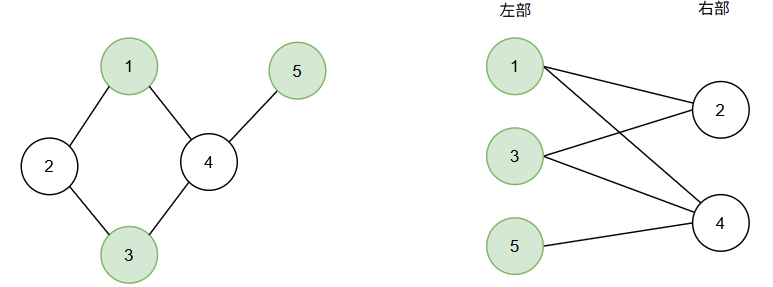
那么矩阵中不同行不同列的元素怎么和二分图挂钩？把矩阵的行和列分别看成二分图的左部和右部，二分图的每条边可以看成是行和列的匹配，不同行不同列的元素就是一组没有公共节点的边，比如上图中的边（1，2）和（1，4）就公用了左部（行）中的顶点1，就不匹配结果。只要在 NxM （左部包含N个顶点，右部包含M个顶点）二分图中找到 N 个不公用顶点的边的集合，就等价于在 NxM矩阵中找到 N 个不同行不同列的元素的一个组合。如下图用例：

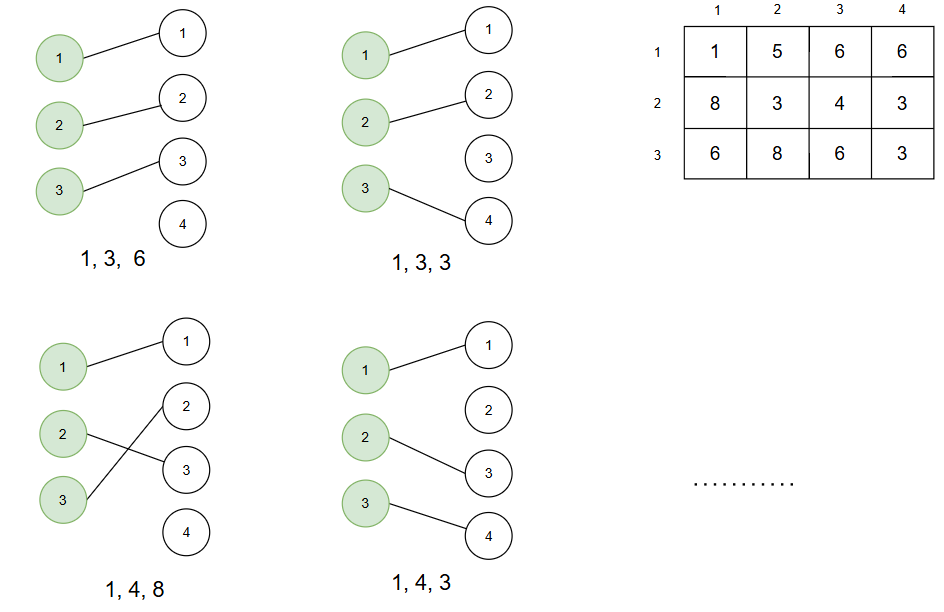
假设已经构建了二分图，理论上可以找到多种这样的匹配。但若逐一列出所有匹配并比较其中第 K 大的元素，还是暴力解法，效率低下。转换思路，我们假设已知第 K 大元素的最小值为 kth。那么，矩阵中至多有 N−K+1 个元素值 ≤kth，且这些元素需互不同行同列。因为在这 N 个元素中，有 K−1 个元素比 kth 大，剩下的 N−(K−1)=N−K+1 个元素 ≤kth，这 N−K+1 个元素中包含了 kth（第 K 大值）本身。

kth 的大小和二分图的最大匹配数存在正相关关系。当 kth 越小时，满足 ≤kth 的矩阵元素就越少；而 kth 越大，满足 ≤kth 的元素就越多。基于这种关系，我们可以采用二分法来枚举 kth 的值。二分枚举的范围是 1 到矩阵元素的最大值。即使枚举到的 kth 不是矩阵中的元素也无需担心，最终我们要找到的第 K 大元素必然收敛到矩阵中的某个值。在二分枚举过程中，若当前枚举的 kth 值使得二分图的最大匹配数 ≥N−K+1，则说明 kth 取大了，应将二分的右边界缩小为 kth - 1；反之，若最大匹配数 < N−K+1，则 kth 取小了，需将二分的左边界扩大为 kth + 1。如此反复，即可高效地找到满足条件的第 K 大元素的最小值。

为什么 `mid` 不在矩阵中也没关系？

假设 mid 是一个不在矩阵中的值（例如矩阵中有 5 和 7，mid=6）：

若 mid=6 满足条件（即存在足够多的元素 ≤ 6），说明一定存在比 6 小的矩阵元素也满足条件（比如 5）。因此算法会向左收缩（right=mid-1），继续寻找更小的可行值。
若 mid=6 不满足条件，说明需要更大的值（至少 7），算法会向右收缩（left=mid+1）。

通过这种收缩，最终的 ans 一定会落到矩阵中的某个元素上。因为：

初始的 left 和 right 是矩阵中的最小值和最大值（min(...flat) 和 max(...flat)），区间内包含所有可能的候选值。
当区间收缩到 left = right 时，这个值必然是矩阵中的元素（因为初始范围是矩阵元素的范围，且每次收缩都基于整数步长）。

求解 NxM 矩阵中找到 N 个不同行不同列的元素的排列数转为求二分图边的最大匹配数，最大匹配表明至少为 N （N<=M) 条边满足不公用顶点，满足题目要求。求二分图边最大匹配数用增广路径算法可实现在 O(VE) 复杂度内完成，优于暴力解法的 O(P(M, N))，P(M,N) 表示在M中任取N个元素的全排列数量。

增广路径算法的核心是通过寻找增广路径来扩展匹配：

增广路径：指从一个未匹配的左部节点出发，交替经过未匹配边和匹配边，最终到达一个未匹配的右部节点的路径。
扩展匹配：找到增广路径后，将路径上的 “未匹配边” 改为 “匹配边”，“匹配边” 改为 “未匹配边”，即可使匹配数增加 1。

通过不断寻找增广路径并扩展匹配，直到无法找到新的增广路径，此时的匹配即为最大匹配。

我们以给定的 3×4 矩阵为例，用增广路径算法求解最大匹配数。首先需要明确：二分图的左部为矩阵的行（3 个节点：R0、R1、R2），右部为矩阵的列（4 个节点：C0、C1、C2、C3），每行与每列都有边（因为矩阵每个位置都有元素）。

增广路径算法流程（分步解析）

初始状态

匹配关系：无任何匹配（用 match_to[v] = -1 表示列 v 未匹配，v=0,1,2,3）
匹配数：0

第 1 步：处理行节点 R0（左部第 1 个节点）

目标：为 R0 找到一个未匹配的列，形成匹配。

遍历 R0 可连接的列（C0、C1、C2、C3，矩阵每行都有 4 列）。
先尝试 C0：C0 未匹配（match_to[0] = -1），直接匹配 R0-C0。
- 更新匹配关系：match_to[0] = 0（C0 匹配 R0）
- 匹配数变为 1。

当前匹配：R0-C0

第 2 步：处理行节点 R1（左部第 2 个节点）

目标：为 R1 找到匹配，若目标列已被匹配，则尝试让已匹配的行 “让贤”。

遍历 R1 可连接的列（C0、C1、C2、C3）。
先尝试 C0：C0 已匹配 R0（match_to[0] = 0），需检查 R0 是否能换其他列。
- 标记 C0 为已访问（避免重复检查）。
- 让 R0 尝试其他列（C1、C2、C3），发现 C1 未匹配（match_to[1] = -1）。
- 解除 R0-C0 的匹配，改为 R0-C1，此时 C0 变为未匹配。
R1 匹配 C0：
- 更新匹配关系：match_to[1] = 0（C1 匹配 R0），match_to[0] = 1（C0 匹配 R1）
- 匹配数变为 2。

当前匹配：R0-C1，R1-C0

第 3 步：处理行节点 R2（左部第 3 个节点）

目标：为 R2 找到匹配，若列已被匹配，递归让已匹配的行换列。

遍历 R2 可连接的列（C0、C1、C2、C3）。
先尝试 C0：C0 已匹配 R1（match_to[0] = 1），检查 R1 是否能换列。
- 标记 C0 为已访问。
- R1 尝试其他列（C1、C2、C3），C1 已匹配 R0（match_to[1] = 0），检查 R0 是否能换列。
  - 标记 C1 为已访问。
  - R0 尝试其他列（C2、C3），C2 未匹配（match_to[2] = -1）。
  - 解除 R0-C1 的匹配，改为 R0-C2，此时 C1 变为未匹配。
- R1 可以匹配 C1（此时 C1 已未匹配），解除 R1-C0 的匹配，改为 R1-C1，此时 C0 变为未匹配。
R2 匹配 C0：
- 更新匹配关系：match_to[2] = 0（C2 匹配 R0），match_to[1] = 1（C1 匹配 R1），match_to[0] = 2（C0 匹配 R2）
- 匹配数变为 3。

当前匹配：R0-C2，R1-C1，R2-C0

最终结果

所有行节点（3 个）都已匹配，最大匹配数为 3。

解决了计算二分图最大匹配数问题，我们就可以通过二分查找搜索最小的 kth，这个二分查找也称为二分答案，就是通过二分查找来猜答案。

算法过程

输入处理：读取输入的矩阵维度（N, M, K）和矩阵数据。
二分搜索初始化：确定搜索范围，左边界为矩阵最小值，右边界为矩阵最大值。
二分搜索过程：
- 构建二分图：对于当前候选值mid，构建一个二分图，其中边表示矩阵中小于等于mid的元素位置。
- 增广路径算法：计算二分图的最大匹配数，即最多可以选择多少个不同行和列的小于等于mid的元素。
- 判定条件：如果最大匹配数至少为N-K+1，说明当前mid可行，记录并尝试更小的mid值；否则，尝试更大的mid值。
输出结果：最终输出的ans即为满足条件的第K大数字的最小值。
时间复杂度约 O(N²M log(maxVal))

参考代码

// 二分图最大匹配（增广路径算法）解法
function solution(N, M, K, mtx) {
  // 构建二分图
  const buildGraph = mid => {
    const graph = Array.from({ length: N }, () => []);
    for (let i = 0;  i < N; i++) {
      for (let j = 0; j < M; j++) {
        if (mtx[i][j] <= mid) {
          graph[i].push(j);
        }
      }
    }
    return graph;
  };

  // 求二分图最大匹配数
  const bipartieMaxMatch = graph => {
    const matchTo = Array(M).fill(-1); // M是列，初始化为-1表示列都未匹配
    let result = 0;

    const dfs = (u, visited) => {
      for (const v of graph[u]) { // 遍历当前行u对应的每列
        if (!visited[v]) { 
          visited[v] = true; //标记 v 为已访问（避免重复检查)
          // 当前列未匹配就直接匹配，否则递归查找已匹配的matchTo[v]能否换列
          if (matchTo[v] === -1 || dfs(matchTo[v], visited)) {
            matchTo[v] = u; // 更新匹配关系
            return true;
          }
        }
      }
      return false;
    };

    for (let u = 0; u < N; u++) { // 遍历每一行，每条边的起点，目标是为当前行找到一个未匹配的列，形成匹配
      const visited = Array(M).fill(false);
      if (dfs(u, visited)) {
        result++; //找到一条增广路径，匹配数+1
      }
    }
    return result;

  };

  const flat = mtx.flat();
  let left = Math.min(...flat);
  let right = Math.max(...flat);
  let ans = right;

  while (left <= right) {
    const mid = Math.floor(left + (right - left) / 2);
    const graph = buildGraph(mid);
    const maxMatch = bipartieMaxMatch(graph);

    if (maxMatch >= N - K + 1) {
      ans = mid;
      right = mid - 1;
    } else {
      left = mid + 1;
    }

  }

  return ans;
}


function entry() {
  let [N, M, K] = readline().split(" ").map(Number);
  const mtx = [];
  for (let i = 0; i < N; i++) {
    mtx[i] = readline().split(" ").map(Number);
  }

  const result = solution(N, M, K, mtx);
  console.log(result);
}


const cases = [
  `3 4 2
1 5 6 6
8 3 4 3
6 8 6 3`,
`10 15 6
112 47 62 99 54 87 129 60 12 59 12 38 128 65 18
88 124 17 37 69 144 66 91 6 42 2 108 121 150 29
28 132 90 110 132 146 139 61 12 71 8 143 82 83 48
105 39 48 54 40 107 22 3 52 20 6 23 26 56 146
108 67 54 40 42 51 140 26 122 16 124 97 132 58 35
16 105 102 114 98 81 107 83 18 103 80 65 88 35 11
100 85 150 138 112 31 140 89 68 128 68 54 7 87 148
95 134 143 25 69 104 76 4 21 70 93 110 117 18 74
49 131 82 81 80 37 110 20 79 119 103 85 31 84 11
5 34 103 71 75 61 85 79 95 49 139 139 66 12 125`
];

(function() {
  function generateMtx(N, M, K) {
    if (N > M) {
      throw Error("N must be greater than M.");
    }
    if (K > N) {
      throw Error("K must be less than N.");
    }
    let s = `${N} ${M} ${K}`;
    let mtx = [];
    for (let i = 0; i < N; i++) {
      let row = Array(M).fill(0).map(() => 1 + Math.round(Math.random() * N * M));
      mtx.push(row.join(' '));
    }
    s += '\n' + mtx.join('\n');
    return s;
  }

  cases.push(generateMtx(30, 35, 10));
}());




let caseIndex = 0;
let lineIndex = 0;

const readline = (function () {
  let lines = [];
  return function () {
    if (lineIndex === 0) {
      lines = cases[caseIndex]
        .trim()
        .split("\n")
        .map((line) => line.trim());
    }
    return lines[lineIndex++];
  };
})();

cases.forEach((_, i) => {
  caseIndex = i;
  lineIndex = 0;
  entry();
  console.log('-------');
});