【LeetCode 热题100道笔记】柱状图中最大的矩形

题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 1:

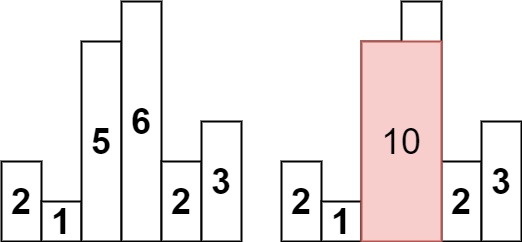
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

示例 2：

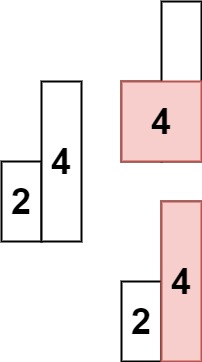
输入： heights = [2,4]
输出： 4

提示：

• $1<=heights.length<=10^5$
• $0<=heights[i]<=10^4$

思考

采用单调栈算法，核心思想是：对于每个柱子，找到其左侧和右侧第一个高度小于它的柱子，以当前柱子高度为矩形高度，两侧边界距离为宽度，计算面积并更新最大值。通过单调栈可高效确定每个柱子的左右边界，避免暴力枚举过高的时间开销。

算法过程

1. 初始化栈与最大面积：

   • 栈中初始存入 -1（作为左边界的哨兵，简化边界判断）。
   • maxArea 记录最大矩形面积（初始为0）。

2. 正向遍历数组（确定右边界）：

   • 对每个柱子索引 i：
     • 若栈顶元素不是 -1 且当前柱子高度 heights[i] 小于栈顶索引对应的柱子高度：
       • 弹出栈顶索引 curHeightIndex（以该索引对应的柱子为当前计算高度）。
       • 计算宽度：i - 栈顶索引 - 1（栈顶索引为左侧第一个矮于当前高度的柱子，i 为右侧第一个矮于当前高度的柱子）。
       • 计算面积 height × width，更新 maxArea。
     • 将当前索引 i 入栈（维持栈的单调性）。

3. 处理栈中剩余元素（确定左边界）：

   • 遍历结束后，栈中仍有除 -1 外的索引（这些柱子右侧无更矮的柱子，右边界为数组长度 n）。
   • 依次弹出栈顶索引 i：
     • 高度为 heights[i]。
     • 宽度为 n - 栈顶索引 - 1。
     • 计算面积并更新 maxArea。

4. 返回结果：maxArea 即为最大矩形面积。

时空复杂度分析

• 时间复杂度：O(n)，每个柱子最多入栈和出栈各一次，总操作次数为O(n)。
• 空间复杂度：O(n)，栈的最大长度为n（当柱子高度单调递增时，所有索引入栈）。

代码

/**
 * @param {number[]} heights
 * @return {number}
 */
var largestRectangleArea = function(heights) {
    const n = heights.length;
    const stack = [-1];
    let maxArea = 0;
    for (let i = 0; i < n; i++) {
       while (stack[stack.length - 1] !== -1 && heights[i] < heights[stack[stack.length - 1]]) {
           const curHeightIndex = stack.pop();
           const height = heights[curHeightIndex];
           const width = i - stack[stack.length-1]-1;
           maxArea = Math.max(maxArea, width * height);
       }
       stack.push(i);
    }

    while (stack.length > 1) {
        const i = stack.pop();
        const height = heights[i];
        const width = n - stack[stack.length-1]-1;
        maxArea = Math.max(maxArea, width * height);
    }

    return maxArea;    
};