【LeetCode热题100道笔记】二叉树中的最大路径和

题目描述

二叉树中的 路径 被定义为一条节点序列，序列中每对相邻节点之间都存在一条边。同一个节点在一条路径序列中 至多出现一次 。该路径 至少包含一个 节点，且不一定经过根节点。
路径和 是路径中各节点值的总和。
给你一个二叉树的根节点 root ，返回其 最大路径和 。

示例 1：

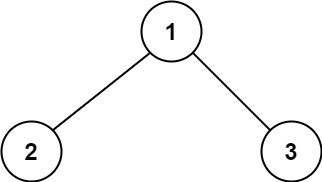
输入：root = [1,2,3]
输出：6
解释：最优路径是 2 -> 1 -> 3 ，路径和为 2 + 1 + 3 = 6

示例 2：

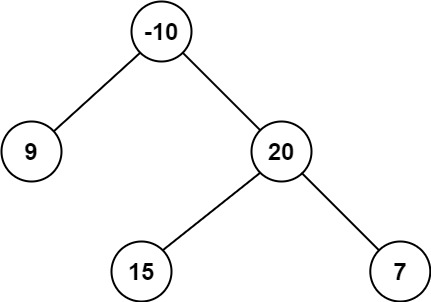
输入：root = [-10,9,20,null,null,15,7]
输出：42
解释：最优路径是 15 -> 20 -> 7 ，路径和为 15 + 20 + 7 = 42

提示：
树中节点数目范围是 [1, 3 * 104]
-1000 <= Node.val <= 1000

思考

递归计算每个子树的最长路径，注意分类讨论不能遗漏：根节点本身是最大路径和、左子树最大路径和不包含根节点、左子树最大路径和包含根节点、右子树最大路径和不包含根节点、右子树最大路径和包含根节点、最大路径和跨越左右子树和根节点。

算法过程

1. 初始化全局最大路径和：定义 maxSum 并设为负无穷，用于存储整棵树的最大路径和（应对节点值全为负数的场景）。
2. 递归函数定义与终止条件：
   定义 pathSum 函数，输入为当前节点，返回“以当前节点为起点，向父节点延伸的最大路径和”（即当前节点对上层的“贡献值”）；若当前节点为 null，返回 0（空节点对路径和无贡献）。
3. 计算左右子树贡献值：
   递归调用 pathSum 分别计算左子树（leftSum）和右子树（rightSum）的贡献值，直接使用原始计算结果（不主动过滤负数，后续通过比较涵盖负数场景）。
4. 更新全局最大路径和：
   考虑所有可能的路径情况，用以下值的最大值更新 maxSum：
   • 全局当前 maxSum（保留历史最大值）；
   • 当前节点值本身（路径仅含当前节点）；
   • 当前节点值 + 左子树贡献值（路径含当前节点和左子树）；
   • 当前节点值 + 右子树贡献值（路径含当前节点和右子树）；
   • 左子树贡献值 + 当前节点值 + 右子树贡献值（路径跨越左右子树和当前节点）。
5. 返回当前节点的贡献值：
   贡献值取“当前节点值”“当前节点值+左子树贡献值”“当前节点值+右子树贡献值”中的最大值（确保向父节点延伸时，传递的是最优路径和）。
6. 最终结果处理：
   调用 pathSum(root) 触发递归后，返回 maxSum 与递归返回值 sum 的最大值（覆盖所有可能的路径场景，确保结果正确）。

时空复杂度

• 时间复杂度：O (n)，n 为二叉树节点总数。
  原因：每个节点仅被访问 1 次（后序遍历），每个节点的计算操作（更新贡献值和最大和）均为 O (1)，总时间与节点数线性相关。
• 空间复杂度：O (h)，h 为二叉树高度。
  原因：递归调用栈深度取决于树高，平衡树 h=O (log n)，链状树 h=O (n)。

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxPathSum = function(root) {
    let maxSum = -Infinity;
    const pathSum = function(node) {
        if (!node) return 0;
        let val = node.val;
        let leftSum = pathSum(node.left);
        let rightSum = pathSum(node.right);

        maxSum = Math.max(maxSum, val, val + leftSum, val + rightSum, leftSum + val + rightSum);
        
        return Math.max(val, leftSum + val, rightSum + val);
    };
    const sum = pathSum(root);
    return Math.max(maxSum, sum); 
};