【LeetCode热题100道笔记】二叉树的最大深度

题目描述

给定一个二叉树 root ，返回其最大深度。
二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

示例 1：

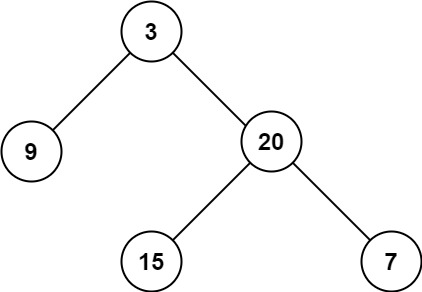
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2：
输入：root = [1,null,2]
输出：2

提示：
树中节点的数量在 $[0,10^4]$ 区间内。
-100 <= Node.val <= 100

思考一：深度优先搜索

二叉树的“最大深度”定义为从根节点到最远叶子节点的最长路径上的节点数。从递归视角看，根节点的深度由其左右子树的深度决定：

1. 若当前节点为空（如叶子节点的左/右子树），其深度为0（递归终止条件）；
2. 若当前节点非空，需先递归计算左子树的最大深度和右子树的最大深度；
3. 当前节点的深度 = 左右子树深度的最大值 + 1（“+1”是因为要包含当前节点本身）；
4. 从根节点开始递归，最终返回的就是整棵树的最大深度。

该思路通过“自下而上”的回溯，将整棵树的深度问题拆解为子树的深度问题，符合深度优先搜索“深入子节点再回溯”的核心逻辑。

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function(root) {
    if (!root) return 0;
    return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;    
};

思考二：广度优先搜索

广度优先搜索以“层”为单位遍历二叉树，而二叉树的“层数”恰好等于其“最大深度”（根节点为第1层，子节点为第2层，以此类推）。因此可通过统计遍历的层数来获取最大深度：

1. 若根节点为空，深度为0（边界条件）；
2. 用队列存储当前层的所有节点，初始时队列仅包含根节点，层数计数器count初始为0；
3. 循环处理每一层：
   • 新建临时数组tmp，用于存储下一层的所有节点；
   • 遍历当前队列，弹出每个节点，将其左、右子节点（若存在）加入tmp；
   • 当前层处理完毕后，将队列更新为tmp，层数计数器count加1；
4. 当队列为空时，所有层已遍历完毕，count即为整棵树的最大深度。

该思路通过“自上而下”的层序遍历，直接将“深度”转化为“层数”，无需递归，适合处理深度较大的树（避免栈溢出）。

代码

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var maxDepth = function(root) {
    if (!root) return 0;
    let queue = [root];
    let count = 0;
    while (queue.length) {
        let tmp = [];
        while (queue.length) {
            let p = queue.pop();
            if (p.left) {
                tmp.push(p.left);
            }
            if (p.right) {
                tmp.push(p.right);
            }
        }
        queue = tmp;
        count++;
    }
    return count;
};