【Virtual Globe 渲染技术笔记】4 椭球面上的曲线

椭球面上的曲线

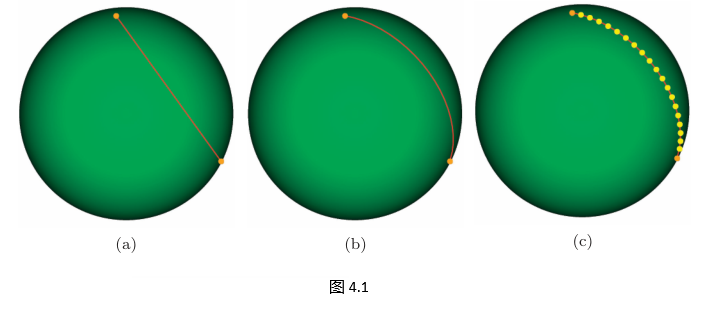
在虚拟地球中，经常需要在椭球面上连接两个端点。
如果直接用直线连接，路径会切入椭球内部（图 4.1$(a)$）。更好的做法是用一系列采样点构造一条“贴”着椭球曲面前进的路径（图 4.1 $(b)$、$(c)$）。

常见曲线类型

• 大地线（geodesic）：两点间最短路径。
• 等角航线（rhumb line）：方位角恒定；虽非最短，却因导航简便而广泛使用。

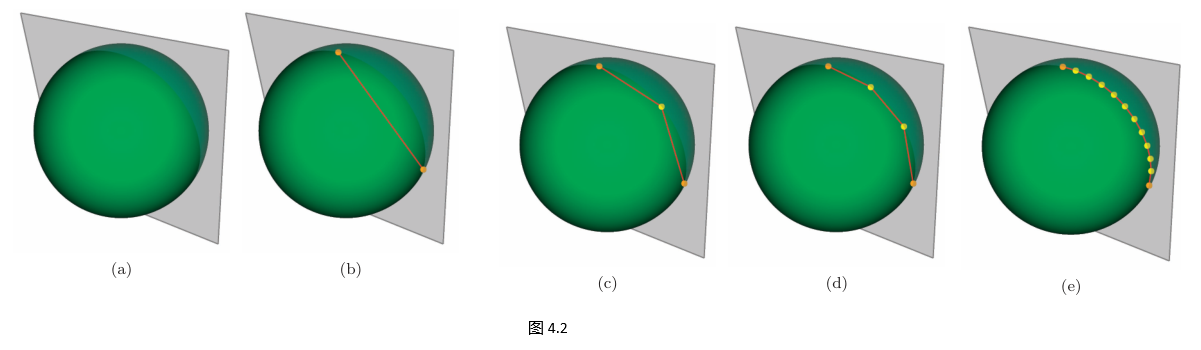
本节介绍一种简单方法：用平面与椭球面相交来生成曲线（图 4.2(a)）。
在球面上，过球心的平面与球面相交得大圆，其短弧即为最短路径。类似地，对接近球形的椭球（如地球扁球），只要端点相距不远，用此法得到的曲线已足够用于渲染。

算法步骤

给定端点 $\mathbf{p},\mathbf{q}$、角度粒度 $\gamma$、椭球 $(a,b,c)$，计算一条以 $\gamma$ 为角间距的采样路径。
如图 4.2(c–e)，$\gamma$ 越小，采样越密，曲线越平滑。

注：除 $\gamma \to 0$ 极限外，线段仍会轻微切入椭球；后续章节将给出一种深度测试策略，使线段仍能被正确绘制。

1. 求平面法向量
   $$\tilde{\mathbf{p}}=\mathbf{p}-0,\tilde{\mathbf{q}}=\mathbf{q}-0,\mathbf{m}=\tilde{\mathbf{p}}\times \tilde{\mathbf{q}},\hat{\mathbf{n}}=\frac{\mathbf{m}}{\Vert \mathbf{m}\Vert }$$

2. 计算端点夹角
   $$\hat{\mathbf{p}}=\frac{\tilde{\mathbf{p}}}{\Vert \tilde{\mathbf{p}}\Vert },\hat{\mathbf{q}}=\frac{\tilde{\mathbf{q}}}{\Vert \tilde{\mathbf{q}}\Vert },\theta =\arccos (\hat{\mathbf{p}}\cdot \hat{\mathbf{q}})$$

3. 采样点数
   $$n=\lfloor \frac{\theta }{\gamma }\rfloor -1,s=\max (n,0)$$

4. 生成采样点
   对每个 $i=0,1,\dots ,s$，取
   $${\varphi }_i=i\gamma$$
   将 $\tilde{\mathbf{p}}$ 绕 $\hat{\mathbf{n}}$ 旋转 ${\varphi }_i$ 得 ${\mathbf{v}}_i$，再用地心缩放把 ${\mathbf{v}}_i$ 缩放到椭球面上，即得第 $i$ 个采样点。
   （使用地心缩放而非大地缩放，可确保点仍在原平面内，从而落在期望曲线上。）

---

思考题
如果不用角度粒度和绕法向量旋转，而是直接对端点做线性插值得到一组点，再对每点调用 scaleToGeocentricSurface，有何优缺点？

• 优点

  • 实现更简单；
  • 采样点在三维空间均匀分布。

• 缺点

  • 插值点不一定共面，生成的曲线可能偏离期望平面；
  • 在椭球高曲率区域，路径可能出现明显扭曲；
  • 均匀线性插值在椭球表面上的角距不均匀，导致视觉密度不一致。

---

参考：

• Cozi, Patrick; Ring, Kevin. 3D Engine Design for Virtual Globes. CRC Press, 2011.