【Virtual Globe 渲染技术笔记】5 曲面细分

曲面细分（Tessellation）

GPU 只能绘制三角形，因此要把一个椭球体渲染成“地球”，必须先计算出一组能近似椭球表面的三角形——这一过程称为曲面细分。本节介绍三种最常用的椭球细分算法，并比较它们的优劣。

---

5.1 细分曲面（Subdivision Surfaces）

核心思想
先在原点构造单位球的网格，再用椭球半径 $(a,b,c)$ 缩放即可得到椭球。这样既简洁又无需三角函数。

步骤

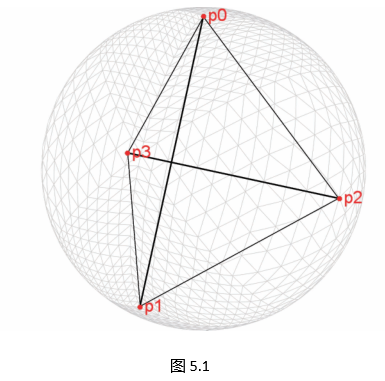
1. 从正四面体开始（图 5.1）。
   顶点坐标：
   $$\begin{array}{rl}{\mathbf{p}}_0& =(0,0,1),\\ {\mathbf{p}}_1& =(0,\frac{2\sqrt{2}}{3},-\frac{1}{3}),\\ {\mathbf{p}}_2& =(-\frac{\sqrt{6}}{3},-\frac{\sqrt{2}}{3},-\frac{1}{3}),\\ {\mathbf{p}}_3& =(\frac{\sqrt{6}}{3},-\frac{\sqrt{2}}{3},-\frac{1}{3}).\end{array}$$

2. 对每个三角形四等分：

   • 取三边中点 ${\mathbf{p}}_{ij}=({\mathbf{p}}_i+{\mathbf{p}}_j)/2$；
   • 归一化到单位球面：${\mathbf{p}}_{ij}\leftarrow {\mathbf{p}}_{ij}/\Vert {\mathbf{p}}_{ij}\Vert$。
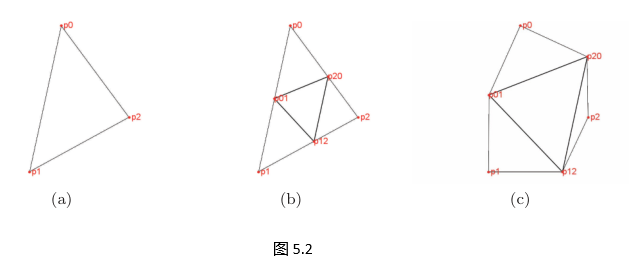
     结果得到 4 个新的几乎等边三角形（图 5.2）。
     

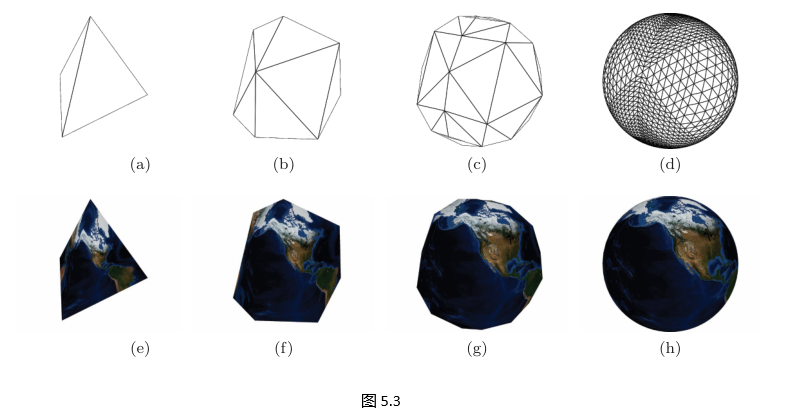
3. 递归执行，直到满足停止条件（递归深度 $n$）。

   • $n$ 次细分后三角面数为 $4^{n+1}$。
   • 深度越大，网格越密（图 5.3），但计算与显存开销也随之增加。
     

LOD（细节层次）

• 视角靠近时可用大 $n$；
• 视角远离时减小 $n$ 以节省资源。

替代拓扑
正四面体只有 4 个面；使用更多面的正多面体（八面体、二十面体）可减少所需细分次数，但实现复杂度略增。

---

5.2 细分曲面实现（Subdivision-Surfaces Implementation）

• 先创建包含 4 个初始顶点的 Mesh。
• 递归函数 Subdivide负责：
  1. 若 level == 0：直接记录当前三角形索引；
  2. 否则：计算三条边中点→归一化→递归细分 4 次。
• 顶点顺序始终为逆时针，确保正面剔除方向一致。

实现代码

Mesh* SubdivisionSphereTessellatorSimple::compute(int numberOfSubdivisions) {
        if (numberOfSubdivisions < 0) {
            throw std::out_of_range("numberOfSubdivisions");
        }

        Mesh* mesh = new Mesh();
        mesh->setPrimitiveType(PrimitiveType::Triangles);
        mesh->setFrontFaceWindingOrder(WindingOrder::Counterclockwise);

        size_t vertexCount = SubdivisionUtility::numberOfVertices(numberOfSubdivisions);
        VertexAttributeDoubleVector3* positionsAttribute = new VertexAttributeDoubleVector3("position", vertexCount);
        mesh->attributes()->add(positionsAttribute);

        size_t indexCount = 3 * SubdivisionUtility::numberOfTriangles(numberOfSubdivisions);
        IndicesUnsignedInt* indices = new IndicesUnsignedInt(indexCount);
        mesh->setIndices(indices);

        double negativeRootTwoOverThree = -std::sqrt(2.0) / 3.0;
        const double negativeOneThird = -1.0 / 3.0;
        double rootSixOverThree = std::sqrt(6.0) / 3.0;

        std::vector<glm::dvec3>& positions = positionsAttribute->values();
        positions.push_back(glm::dvec3(0.0, 0.0, 1.0));
        positions.push_back(glm::dvec3(0.0, (2.0 * std::sqrt(2.0)) / 3.0, negativeOneThird));
        positions.push_back(glm::dvec3(-rootSixOverThree, negativeRootTwoOverThree, negativeOneThird));
        positions.push_back(glm::dvec3(rootSixOverThree, negativeRootTwoOverThree, negativeOneThird));

        subdivide(positions, *indices, TriangleIndicesUnsignedInt(0, 1, 2), numberOfSubdivisions);
        subdivide(positions, *indices, TriangleIndicesUnsignedInt(0, 2, 3), numberOfSubdivisions);
        subdivide(positions, *indices, TriangleIndicesUnsignedInt(0, 3, 1), numberOfSubdivisions);
        subdivide(positions, *indices, TriangleIndicesUnsignedInt(1, 3, 2), numberOfSubdivisions);

        return mesh;
    }

    void SubdivisionSphereTessellatorSimple::subdivide(std::vector<glm::dvec3>& positions,
                                                       IndicesUnsignedInt& indices,
                                                       const TriangleIndicesUnsignedInt& triangle,
                                                       int level) {
        if (level > 0) {
            glm::dvec3 mid01 = (positions[triangle.I0()] + positions[triangle.I1()]) * 0.5;
            mid01 = glm::normalize(mid01);
            positions.push_back(mid01);

            glm::dvec3 mid12 = (positions[triangle.I1()] + positions[triangle.I2()]) * 0.5;
            mid12 = glm::normalize(mid12);
            positions.push_back(mid12);

            glm::dvec3 mid20 = (positions[triangle.I2()] + positions[triangle.I0()]) * 0.5;
            mid20 = glm::normalize(mid20);
            positions.push_back(mid20);

            int i01 = static_cast<int>(positions.size()) - 3;
            int i12 = static_cast<int>(positions.size()) - 2;
            int i20 = static_cast<int>(positions.size()) - 1;

            --level;
            subdivide(positions, indices, TriangleIndicesUnsignedInt(triangle.I0(), i01, i20), level);
            subdivide(positions, indices, TriangleIndicesUnsignedInt(i01, triangle.I1(), i12), level);
            subdivide(positions, indices, TriangleIndicesUnsignedInt(i01, i12, i20), level);
            subdivide(positions, indices, TriangleIndicesUnsignedInt(i20, i12, triangle.I2()), level);
        } else {
            indices.addTriangle(triangle);
        }
    }

---

5.3 立方体贴图细分（Cube-Map Tessellation）

思路
把一个轴对齐并绕 z 轴旋转 45° 的单位立方体先均匀细分，再把每个顶点透视投影到椭球面（先归一化，再乘半径 $(a,b,c)$）。

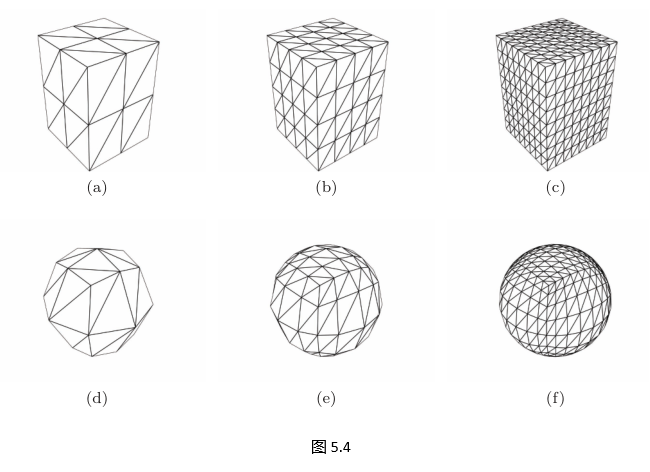
• 立方体 6 个面，每个面先划分成规则网格（2×2、4×4、8×8…）（图 5.4(a–c)）。
• 网格越密，椭球近似越精细（图 5.4(d–f)）。
• 直线在立方体面上→椭球面上变为“类测地”曲线，非经纬线，但极点无过度细分。

实现
CubeMapEllipsoidTessellator::compute 接收椭球参数、网格分区数、顶点属性需求，返回网格。
步骤：

1. 生成 8 个角点；
2. 在 12 条边上插入中间点；
3. 逐行细分每个面；
4. 最后将点投影到椭球并计算法线/纹理坐标。

---

5.4 经纬网格细分（Geographic-Grid Tessellation）

两步法

1. 生成点
   嵌套循环：

   • 纬度 $\phi \in [0,\pi ]$，经度 $\theta \in [0,2\pi ]$
   • 步长可分别设置
     用球坐标转笛卡尔：
     $$\begin{array}{rl}x& =a\cos \theta \sin \phi ,\\ y& =b\sin \theta \sin \phi ,\\ z& =c\cos \phi .\end{array}$$
     极点特殊处理：$\phi =0,\pi$ 时各用一个顶点 $(0,0,\pm c)$。

2. 生成索引

   • 极区用三角形扇（triangle fan）；
   • 其余行用三角形条带（triangle strip）。

图 5.5 展示不同密度的网格；图 5.6 显示极点处三角形过密。

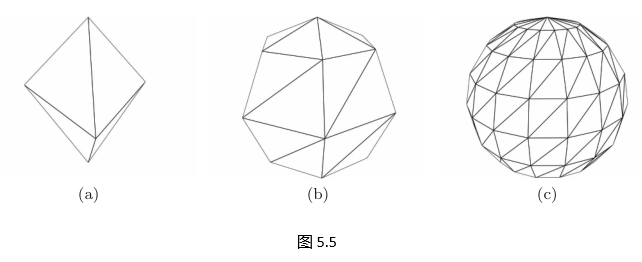
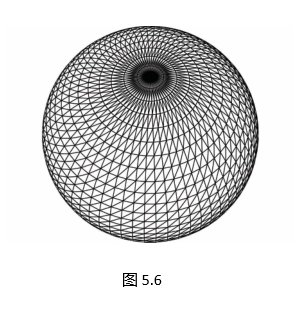
优缺点

• 实现直观；
• 避免跨越国际日期变更线（IDL）；

缺点：

• 极点三角形极细，导致光照/纹理伪影、片段冗余、裁剪效率低。
  可通过按纬度调节密度（如按 $\sin \phi$ 缩放）缓解。

---

5.5 三种算法对比

特性	细分曲面	立方体贴图	经纬网格
极点过采样	无	无	有（可调）
跨 IDL 三角形	有（可处理）	有（可处理）	无
实现复杂度	低	中	低
三角形形状	接近等边	面中央好，角部略畸变	纬度低处好，近极细长
典型应用	Spore 星球	NASA World Wind（实验版）	早期 World Wind、STK、Insight3D

没有绝对的“最佳”方案；根据需求（极点质量、实现难度、LOD 灵活性）选择即可。

---

参考：

• Cozi, Patrick; Ring, Kevin. 3D Engine Design for Virtual Globes. CRC Press, 2011.