【Virtual Globe 渲染技术笔记】1 虚拟地球坐标系

最新推荐文章于 2025-12-09 16:25:48 发布

原创最新推荐文章于 2025-12-09 16:25:48 发布 · 857 阅读

19 ·

CC 4.0 BY-SA版权

文章标签：

#笔记 #图形渲染 #GIS

GIS 专栏收录该内容

22 篇文章

订阅专栏

概述

精确渲染虚拟地球的核心在于对地球的椭球体表示。本章将介绍这种表示方法的设计动机与相关数学原理，重点是构建一个可复用的“椭球体（Ellipsoid）”类，该类包含计算表面法向量、进行坐标系转换、求解椭球体表面曲线等多种功能。

本章包含大量的数学知识和推导过程，实现虚拟地球仪并不需要记住本章中的推导过程，相反，目标是形成对这些数学知识的宏观理解与认知，并掌握如何使用本章介绍的椭球体方法。

1.1 虚拟地球坐标系

所有图形引擎都要用到一种或多种坐标系，虚拟地球也不例外。虚拟地球主要涉及两种坐标系：一种是用于指定地球上或相对于地球位置的地理坐标系，另一种是用于渲染的笛卡尔坐标系。

1.1.1 地理坐标系

地理坐标系通过（经度、纬度、高度）三元组来定义地球上的每个位置，这与球坐标系通过（方位角、倾角、半径）三元组定义位置的方式类似。直观来说，经度是从西到东的角度度量，纬度是从南到北的角度度量，高度则是相对于地表的线性距离（可正可负，正为上方，负为下方）。在1.2.3节中，我们会更精确地定义纬度和高度。

地理坐标系应用广泛：大多数矢量数据都基于地理坐标系定义。即便在虚拟地球之外，地理坐标系也被用于全球定位系统（GPS）等领域。

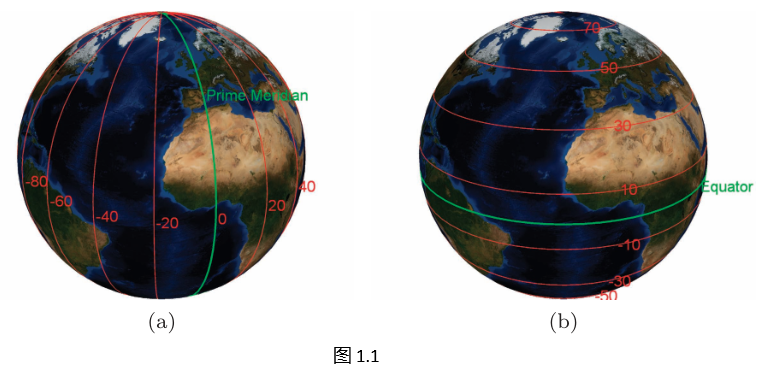
我们采用常用的约定，将经度范围定义为[-180°，180°]。如图1.1（a）所示，本初子午线（西半球与东半球的交界线）处的经度为0°。经度值增大表示向东移动，经度值减小表示向西移动；东半球的经度为正值，西半球的经度为负值。经度值持续增大或减小，最终会到达对向子午线（即±180°经线），这条经线是太平洋上国际日期变更线（IDL）的基准。尽管国际日期变更线在某些地方会为了避开陆地而发生弯折，但在我们的研究范围内，将其近似为±180°经线。许多算法都需要对国际日期变更线进行特殊处理。

经度有时也被定义在[0°，360°]范围内，其中本初子午线处为0°，向东直至国际日期变更线逐渐增大。若要将[0°，360°]范围内的经度转换为[-180°，180°]范围，只需在经度值大于180°时减去360°即可。

纬度是从南到北的角度度量，范围为[-90°，90°]。如图1.1（b）所示，赤道处的纬度为0°，从南到北逐渐增大。北半球的纬度为正值，南半球的纬度为负值。
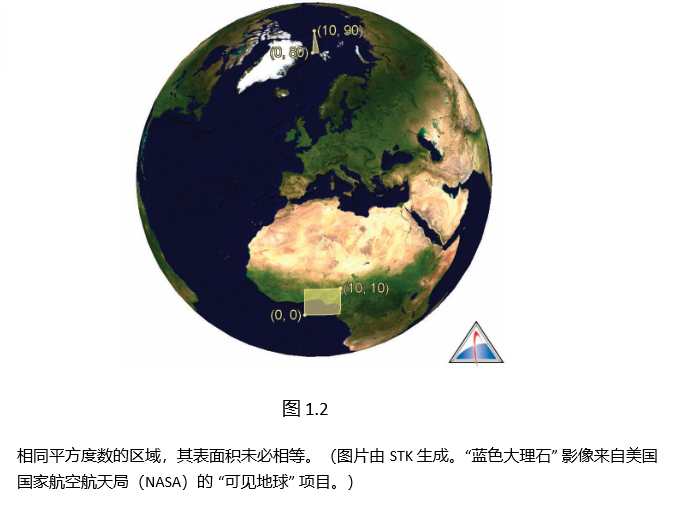
在这里插入图片描述

经度和纬度不应被当作二维笛卡尔坐标系中的x和y坐标来处理。随着纬度逐渐接近极点，等经度线会逐渐汇聚。例如，以（0°，0°）为西南角、（10°，10°）为东北角的区域，其表面积远大于从（0°，80°）到（10°，90°）的区域，尽管两者都是1平方度（见图1.2）。因此，基于均匀经纬度网格的算法在极点附近会出现采样过度的问题，例如1.1.4节中介绍的地理网格细分算法就是如此。
在这里插入图片描述
我们使用度来表示经度和纬度，但代码示例除外——在代码示例中，经度和纬度以弧度表示，因为C++和GLSL函数要求输入弧度。度与弧度之间的转换很简单：一个圆周为2π弧度或360度，因此1弧度等于π/180度，1度等于180/π弧度。经度和纬度有时也用角分和角秒来度量。1度等于60角分，1角分等于60角秒。

在项目中，地理坐标通过Geodetic2D和Geodetic3D来表示，二者的区别在于前者不包含高度信息，默认位置在地表上。
一个静态类Trig提供了toRadians（转换为弧度）和toDegrees（转换为度）这两个转换函数。这些类型的简单示例如代码清单1.1所示。

/*---------------代码清单1.1------------------*/
Geodetic3D p{Trig::toRadians(new Geodetic3D(180.0, 0.0, 5.0));
std::cout << p.longitute() << std::endl;
std::cout << p.latitude() << std::endl;
std::cout << p.height() << std::endl;

Geodetic2D g{Trig::toRadians(new Geodetic2D(180.0, 0.0));
Geodetic2D p2(g, 5.0);

std::cout << p == p2 << std::endl;

1.1.2 WGS84坐标系

地理坐标的优势在于直观——至少对人类而言是这样。但OpenGL无法直接处理地理坐标，它在3D渲染中使用的是笛卡尔坐标。因此，我们需要将地理坐标转换为笛卡尔坐标以进行渲染。

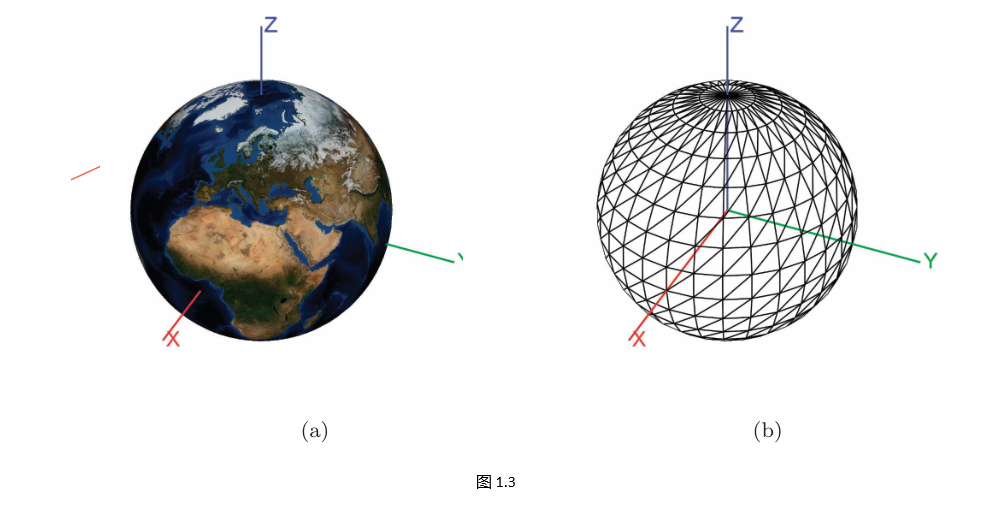
使用的笛卡尔坐标系是1984年世界大地测量系统（WGS84坐标系）。该坐标系与地球相对固定：当地球自转时，该坐标系也随之旋转，因此在WGS84中定义的物体相对于地球保持静止。如图1.3所示，其原点位于地球质心；x轴指向地理坐标（0°，0°）处，y轴指向（90°，0°）处，z轴指向北极；赤道位于xy平面内。这是一个右手坐标系，因此x×y=z（其中x、y、z分别为沿各轴的单位向量）。
在这里插入图片描述

项目中，笛卡尔坐标最常通过 glm::dvec3 来表示。

代码清单1.2展示了归一化、点积、叉积等常见操作的示例代码。

/*----------------代码清单1.2-----------------------*/
#include <glm/glm.hpp>  // 包含GLM库头文件

// 创建三维向量
glm::dvec3 x(1.0, 0.0, 0.0);  // 等同于glm::dvec3(1.0)或glm::dvec3(glm::dvec3::x)
glm::dvec3 y(0.0, 1.0, 0.0);  // 等同于glm::dvec3(glm::dvec3::y)

// 计算向量分量之和
double s = x.x + x.y + x.z;  // 结果为1.0

// 向量运算与归一化
glm::dvec3 n = glm::normalize(y - x);  // 结果为(1.0/sqrt(2.0), -1.0/sqrt(2.0), 0.0)

// 点积计算
double p = glm::dot(n, y);  // 结果为1.0/sqrt(2.0)

// 叉积计算
glm::dvec3 z = glm::cross(x, y);  // 结果为(0.0, 0.0, 1.0)，等同于glm::dvec3(glm::dvec3::z)

可能唯一不熟悉的一点是，glm::dvec 的X、Y、Z分量是双精度浮点数（vec前缀d表示使用双精度），而非大多数图形应用中常用的单精度浮点数。正如第5章所解释的，虚拟地球中使用的大数值（尤其是WGS84坐标中的数值）用双精度表示更为合适。项目还包含适用于2D和4D向量的向量类型，以及单精度浮点数、半精度浮点数（16位）、整数和布尔值等数据类型。

在笛卡尔坐标系中，我们以米为单位；在大地坐标中，高度也以米为单位，这在虚拟地球中是常见做法。

参考：