前缀和——模板 二维前缀和

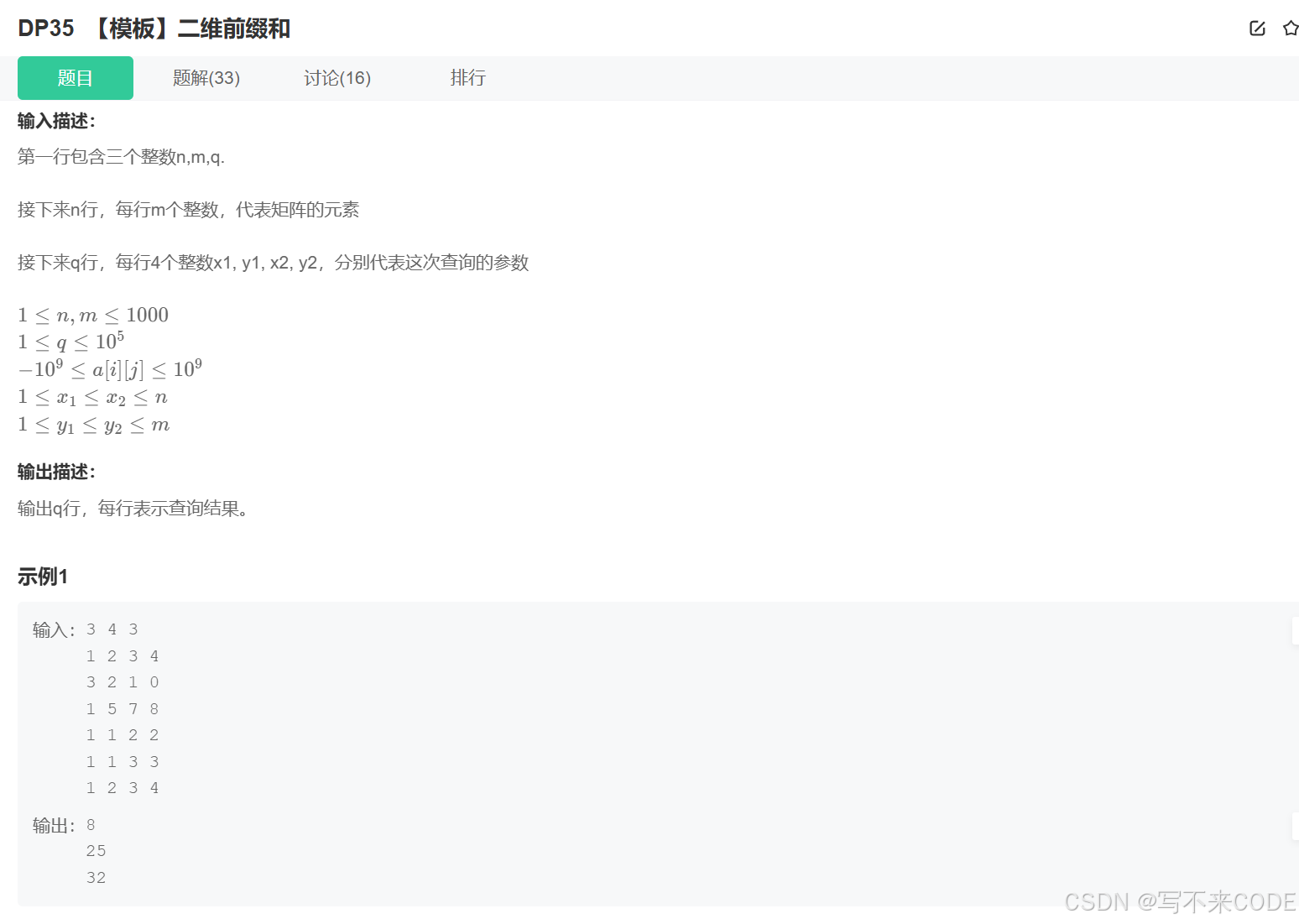
一.题目描述

【模板】二维前缀和_牛客题霸_牛客网

二.题目解析

这道题和上一道题有点异曲同工之妙。输入一个m行n列的矩阵，然后进行q次操作，每次操作输入4个数，作为两个点的坐标，计算这两个点为对角线的矩阵的和。

三.算法原理

1.暴力解法

暴力解法那我们就遍历贝。我们知道了起始下标和结束下标，两个for循环，固定好起始位置和结束位置，即可求出结果。

时间复杂度：最坏情况下，每一次的操作都求出整个矩阵的和，即m*n，所以时间复杂度为O(q*m*N)

空间复杂度：除了用来存储数据的vector外，没有开辟另外的空间，所以空间复杂度为O(1).

2. 前缀和算法

其实这道题和上一道题本质是一样的，都是让我们快速求出一段区间的和。所以我们可以使用前缀和算法来解决。上一道题是一维的数组，所以dp数组也是一维的。而这道题是二维的矩阵，所以我们的dp数组也是二维的矩阵。并且这道题的下标也是从1开始的，就是为了避免边界情况。

2.1初始化前缀和矩阵dp

这里的dp[i][j]表示的是从(1,1)~(i,j)这个区间的和。如果我们用遍历的方法就dp[i][j],那么它的时间复杂度就高了。所以我们得换一种方法：

当我们求dp[i][j]的时候，当前矩阵会被分为4部分。所以我们就是要求这四个部分的和。A区域就是dp[i-1][j-1],D区域其实就是arr[i][j]，现在剩下的就是C和B了。C和B并不是(1,1)位置开始的区间，我们不好求，那么我们就可以转化一下可以求AC和AB。这两个区间的和其实就是dp[]i[j-1]和dp[i-1][j].

但是这会导致多加了一次A，得减去。

所以我们求解dp[i][j] = arr[i][j] + dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1].

2.2使用前缀和数组

 我们所求的区间为(x1,y1)~(x2,y2)，我们怎样将这样区间的和利用上面的dp数组表示出来呢？我们用图将我们所求的区间表示出来：

我们待求的区间是D，而我们无法直接求出D的。我们可以将其看作面积来计算，我们将这整个编面积记作s。D =  s - AC - AB + A。然后我们用dp数组来替换这些面积：D = dp[x2][y2] - dp[x2][y1-1] - dp[x1-1][y2] + dp[x1-1][y1-1].

因为我们这里的下标是从1开始的，所以我们在申请空间的时候，行和列都得多申请一行/列。这里就是为了避免边界情况，下标计算出负数.

2.3复杂度分析 

时间复杂度：处理dp数组时，我们需要遍历一遍数组m*n，接着我们进行q次操作，但是每次操作的时间复杂度都是O(1)，所以综上，前缀和算法的时间复杂度为O(m*n + q).

空间复杂度：该方法除了存储数据的原数组外，还额外开了一个一样大空间的dp数组，所以空间复杂度为O(m*n).

四.代码实现

// C++

#include <iostream>
#include <vector>
using namespace std;

int main()
{
    // 读取数据
    int n = 0, m = 0, q = 0;
    cin >> n >> m >> q;
    vector<vector<long long>> vv(n + 1, vector<long long>(m + 1));
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m; ++j) 
            cin >> vv[i][j];

    // 初始dp矩阵
    vector<vector<long long>> dp(n + 1, vector<long long>(m + 1));
    for (int i = 1; i <= n; ++i)
        for (int j = 1; j <= m; ++j)
            dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + vv[i][j] - dp[i - 1][j - 1];

    // q次操作
    int x1 = 0, y1 = 0, x2 = 0, y2 = 0;
    while (q--)
    {
        cin >> x1 >> y1 >> x2 >> y2;
        cout << dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1] << endl;
    }

    return 0;
}

# python

import sys

# 读取数据
n, m, q = map(int, input().split())
vv = [[0] * (m + 1) for _ in range(n + 1)]
for i in range(1, n + 1):
    vv[i] = list(map(int, input().split()))

# 初始dp矩阵（前缀和矩阵）
dp = [[0] * (m + 1) for _ in range(n + 1)]
for i in range(1, n + 1):
    for j in range(1, m + 1):
        dp[i][j] = dp[i - 1][j] + dp[i][j - 1] + vv[i][j] - dp[i - 1][j - 1]

# q次操作
for _ in range(q):
    x1, y1, x2, y2 = map(int, input().split())
    result = dp[x2][y2] - dp[x1 - 1][y2] - dp[x2][y1 - 1] + dp[x1 - 1][y1 - 1]
    print(result)