前缀和——寻找数组的中心下标

一.题目描述

724. 寻找数组的中心下标 - 力扣（LeetCode）

二.题目解析

题目让我们返回数组的中心下标，中心下标的左右区间的和相等，区间内不包含中心下标本身。如果该数组没有任何一个下标 满足这个要求就返回-1.

就如我们上面的示例1而言：对于第四个数6来说，它的左右区间的和都是11，所以他就是该数组的中心下标。

如果数组中存在多个中心下标，则返回最左侧的。

对于边界情况来说，当中心下标在0或者n-1的位置时，意味着不存在的区间的和为0，另一边的区间和也为0.

就如这个例子，当中心下表标是0时，不存在左区间，所以左区间为0，右区间刚好也为0，所以0就是中心下标 

三.算法原理

1.暴力解法

我们直接根据题意，在遍历到一个数的时候，分别计算它的左边区间和右边区间的和，判断两个是否相等。如果相等直接返回即可，如果遍历完了整个数组都没有返回的话，就返回-1.

时间复杂度：首先我们遍历每一个数据就需要O(n)，每一个数据还需要遍历它的左右区间， 又是一个O(n)，所以总的时间复杂度就是O(n^2)

空间复杂度：只是用了几个变量存储区间的和，所以空间复杂度是O(1)

 2.前缀和

这道题本质上还是需要快速求出一段区间的和，所以我们可以使用前缀和数组。

2.1预处理前缀和数组

我们对于一个元素来说，想要知道它是不是中心下标，得知道它的左右区间的和是否相等。所以我们这里前缀和数组对应的就是左右区间的和。但是一个前缀和数组肯定不够用，所以我们还需要一个后缀和数组。

nums数组：nums[i]表示该位置的元素。

前缀和数组f：f[i] 表示 [0,i-1] 区间的和；

后缀和数组g：g[i]表示 [i+1,n-1]区间的和；

 那如果得到前缀和数组呢？ f[i] = f[i-1] + nums[i-1]

后缀和数组：g[i] = g[i+1] + nums[i+1]

这两个数组的递归公式之所以是这样主要还是因为前缀后缀数组所表示的意义。他们分别表示的是i的左右区间的和。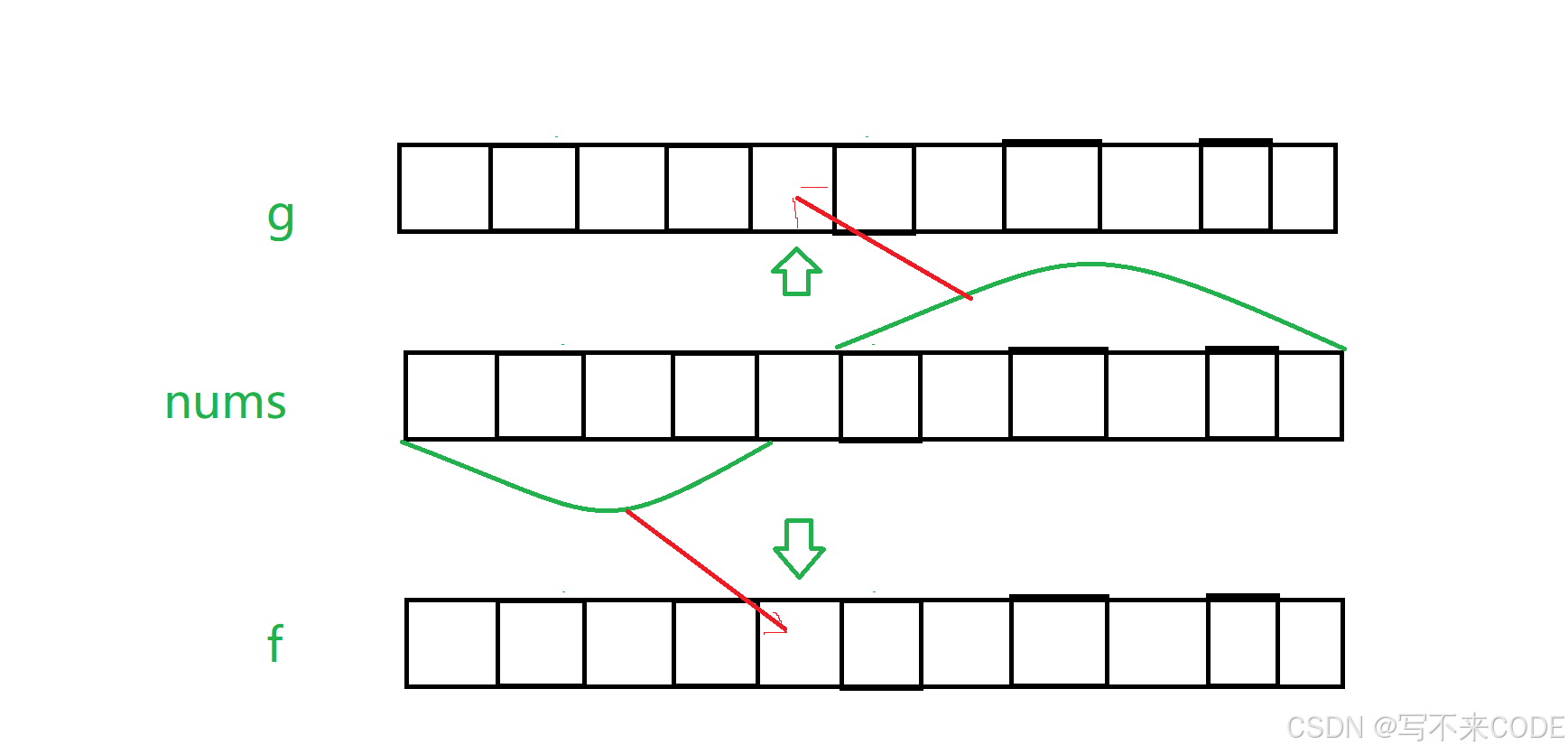 

但因为我们不知道[0,i-1]区间的和， 这个区间的和就等于[0,i-2]的和加上nums[i-1]，所以才有了这样的递归公式，g数组同理。

---

 但f和g数组还有特殊情况，当i为0时，或者i为n-1时，此时f和g数组会出现越界的情况。所以需要进行特殊处理，而这个特殊处理还是很简单的。对于f数组来说，f[0]其实就是0；对于g数组来说，g[n-1]其实也是0.

所以我们直接给这两位置赋值即可，遍历时避开这两个位置。

2.2使用前缀后缀和数组

已经知道了i位置的左区间和为f[i]，右区间的和为g[i]，所以我们只需要遍[0,n-1]这个区间，判断对应的fg是否相等即可，相等直接返回i，如果循环结束还没有返回则直接返回-1.

时间复杂度：处理前后缀和数组需要遍历两边数组，最后寻找中心下标最坏情况下也需要遍历一遍数组，所以时间复杂度为O(n)

空间复杂度：使用了两个数组，空间复杂度为O(n)

3.求和+直接遍历

我们可以先遍历一遍数组求出数组的和total，接着继续遍历原数组，同时记录左区间的和Lsum。当遍历到i位置时，左区间就是Lsum，右区间就是total-Lsum-nums[i]，我们只需要判断这两个值是否相等即可。

在遍历的过程中，Lsum是从0开始一直增加的。 

时间复杂度：整个过程也就只需要遍历两边数组，所以时间复杂度为O(n)

空间复杂度：只利用了几个变量存储区间的和，所以空间复杂度为O(1)

四.代码实现

结合算法原理来看，虽然前缀和算法和求和+遍历都是O(n),但其实后者更优，毕竟少遍历一次数组。且后者空间复杂度还只是O(1).

// C++

// 前缀和
class Solution 
{
public:
    int pivotIndex(vector<int>& nums) 
    {
        int n = nums.size();
        vector<int>f(n),g(n);
        f[0] = 0,g[n-1] = 0;

        // f[i] = (0,i-1)的和
        for(int i=1; i<n; ++i) f[i] = f[i-1] + nums[i-1];

        // g[i] = (i+1,n-1)的和
        for(int i=n-2; i>=0; --i) g[i] = g[i+1] + nums[i+1];

        for(int i=0; i<n; ++i)
            if(f[i] == g[i]) return i;
        return -1;
    }
};

// 求和+遍历
class Solution 
{
public:
    int pivotIndex(vector<int>& nums) 
    {
        int total = accumulate(nums.begin(),nums.end(),0);

        int Lsum = 0;
        int Rsum = 0;
        for(int i=0; i<nums.size(); ++i)
        {
            Rsum = total-Lsum-nums[i];
            if(Lsum == Rsum) return i;
            Lsum += nums[i];
        }
        return -1;
    }
};

# python

# 前缀和
class Solution:
    def pivotIndex(self, nums: List[int]) -> int:
        n = len(nums)
        f, g = [0]*n, [0]*n
        f[0], g[n-1] = 0, 0
        
        for i in range(1, n):
            f[i] = f[i-1] + nums[i-1]

        for i in range(n-2, -1, -1):
            g[i] = g[i+1] + nums[i+1]

        for i in range(n):
            if f[i] == g[i]:
                return i
        return -1



# 求和+遍历
class Solution:
    def pivotIndex(self, nums: List[int]) -> int:
        total,Lsum,Rsum = 0,0,0
        for elem in nums:
            total += elem
        for i in range(0,len(nums)):
            Rsum = total - Lsum - nums[i]
            if Rsum == Lsum:
                return i
            Lsum += nums[i]
        return -1