Open Space代码实现

最新推荐文章于 2025-11-05 22:07:45 发布
原创 最新推荐文章于 2025-11-05 22:07:45 发布 · 537 阅读 · 1 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#memcached

ACE-Step

ACE-Step

音乐合成
ACE-Step

ACE-Step是由中国团队阶跃星辰（StepFun）与ACE Studio联手打造的开源音乐生成模型。 它拥有3.5B参数量，支持快速高质量生成、强可控性和易于拓展的特点。 最厉害的是，它可以生成多种语言的歌曲，包括但不限于中文、英文、日文等19种语言

1.引言

了解Apollo的Open Space算法相关代码，旨在想实现对A星输出的轨迹进行平滑，更专业点可能就是基于最优控制的轨迹优化。先学习整个流程，详细解释其各个部分的作用和原理，最后将原算法的混合A*替换成简单的A*。

  • 代码目录: modules/planning/open_space/.
  • 可视化工具: modules/tools/open_space_visualization/distance_approach_visualizer.py

5.1.混合A*算法

Hybrid A*代码流程图如下:

 

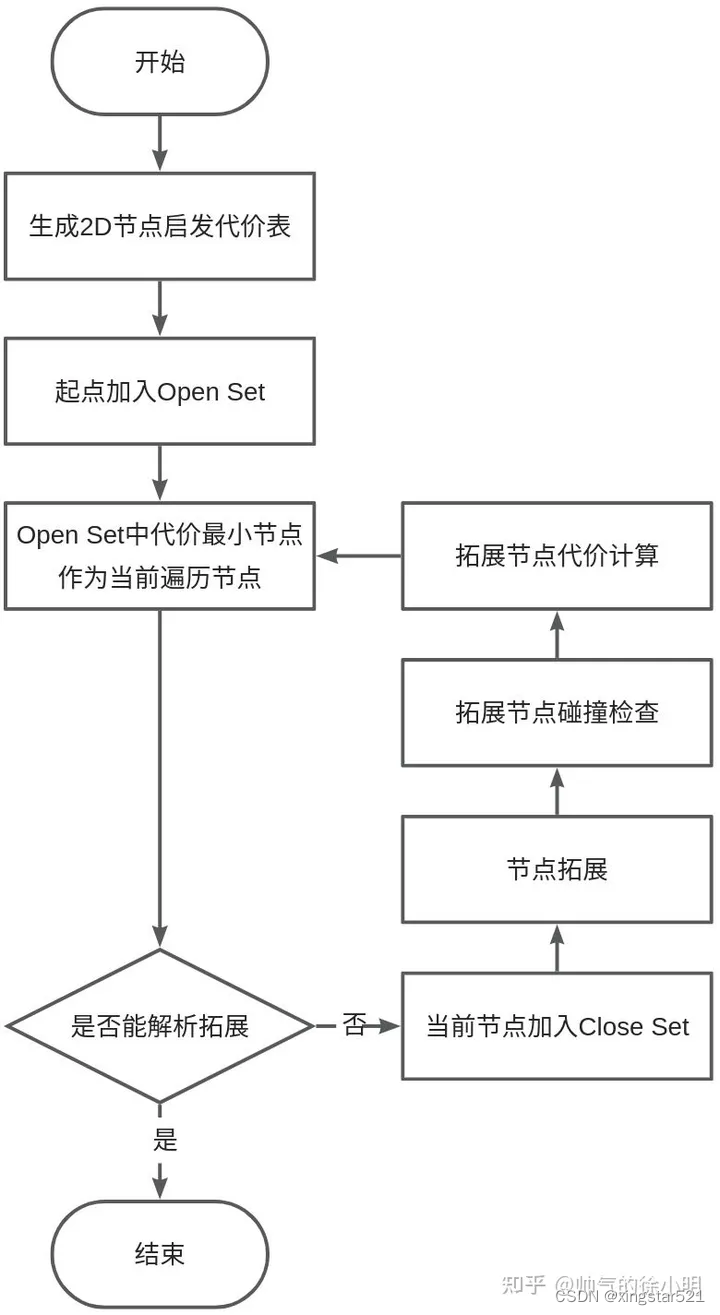
Hybrid A*算法包含了node3d, grid_search, reeds_shepp_path 和 hybrid_a_star. 其中hybrid_a_star是最重要的组成部分, 它调用了grid_search和reeds_shepp_path. 

代码文件在hybrid_a_star.cc中. 函数入口: HybridAStar::Plan, 在OpenSpaceTrajectoryOptimizer::Plan中被调用

您可能感兴趣的与本文相关的镜像

ACE-Step

ACE-Step

音乐合成
ACE-Step

ACE-Step是由中国团队阶跃星辰（StepFun）与ACE Studio联手打造的开源音乐生成模型。 它拥有3.5B参数量，支持快速高质量生成、强可控性和易于拓展的特点。 最厉害的是，它可以生成多种语言的歌曲，包括但不限于中文、英文、日文等19种语言

xingstar521
关注
路径规划-Hybrid A*算法
霍迪迪的博客
03-23 3651
一、算法简介： Hybrid A*算法任然是一种图搜索算法。在A*算法中通常把实际物体当作一个点，不考虑物体的运动方向和物理结构的实际运动。Hybrid A*是2010年由斯坦福大学基于A*改进的算法，Hybrid A*规划的路径考虑了车辆的运动学约束，即满足了车辆的最大曲率约束。
Hybrid A* （混合A*）路径规划算法
qq_29320587的博客
06-21 5015
HybridAStar算法主要是在A* 基础上考虑车辆动力学相关的搜索算法，其放弃了A* 中对搜索空间离散化，利用Dubins或者Reeps-Shepp来考虑自车能够前进的位置，使得规划的轨迹满足车辆的非完整性约束，但是该Hybrid A* 牺牲了算法的完备性和最优性。1.在连续空间上扩张节点搜索最短路径2.路径平滑Hybrid A* 算法与A* 算法的差异对比如下表所示如下图所示，最左侧图是A算法的结果，最右侧是Hybrid A算法。（中间为A* 算法变种）
混合状态 A*小白详解
最新发布
weixin_61287498的博客
11-05 1458
混合A算法是一种改进的路径规划算法，在传统A基础上引入运动学模型，使路径符合无人机动力学约束。该算法通过运动基元替代直线移动，生成符合物理规律的平滑轨迹。相比传统A的网格离散路径和RRT的随机性路径，混合A能产生连续且满足车辆运动学的路径。核心改进包括：使用125个预计算运动基元（由离散加速度组合生成），在速度、加速度等物理约束下进行状态转移，同时利用体素网格地图确保路径安全。搜索过程保持A*框架，通过f=g+h代价函数选择最优路径，其中g包含时间和控制成本，h采用快速估算方法。最终生成的路径既满足无人机动
Apollo规划代码ros移植-混合A*
weixin_39735688的博客
06-09 4089
今天学习移植一下混合A*（Hybrid a）。想要工程代码的看我这一篇： Apollo6.0规划代码ros移植-路径规划可跑工程分享1.A start算法 使用A Star 算法实现自动寻路详解 2.Rs曲线 Reeds-Shepp和Dubins曲线简介[运动规划算法]Dubins曲线和Reeds-Shepp曲线 Hybrid A star是一种带有半径约束的路径平滑规划算法，算法思想来自A算法，但A是没有考虑平滑和半径约束的路径规划算法，且基于栅格地图的网格搜索算法，它们的目标代价函数是为了形成一条路径最
Apollo星火计划学习笔记——Apollo开放空间规划算法原理与实践
sinat_52032317的博客
01-06 9351
1. 开放空间规划算法总体介绍 1.1 Task: OPEN_SPACE_ROI_DECIDER 1.2 Task: OPEN_SPACE_TRAJECTORY_PROVIDER 1.3 Task: OPEN_SPACE_TRAJECTORY_PARTITION 1.4 Task: OPEN_SPACE_FALLBACK_DECIDER 2. 基于混合A *的路径规划算法 2.1 hybrid A*的简要思想 2.2 RS曲线 2.3 Apollo中Hybrid A*算法的求解过程 3. 基于OBCA的轨迹
Apollo Open Space Planner及Hybrid A* 算法入门浅析
牛仔很忙
04-07 6706
Hybrid A* 并不简单！！！
Apollo_ADS_路径规划--Open Space Planner Algorithm 开放空间规划算法-for parking
chepwavege的专栏
07-24 3577
解决： 倒车场景，U 掉头场景 https://github.com/ApolloAuto/apollo/blob/master/docs/specs/Open_Space_Planner.md
Baidu Apollo代码解析之Open Space Planner中的平滑优化
silver bullet
01-19 6345
大家好，我已经把优快云上的博客迁移到了知乎上，欢迎大家在知乎关注我的专栏慢慢悠悠小马车（https://zhuanlan.zhihu.com/c_1132958996826546176）。以后，我会把日常的思考放在优快云上，梳理过的精华文章放在知乎上，希望大家可以多多交流，互相学习。 目录 1、Hybrid A*和平滑优化的效果对比 2、Optimization Smooth...
Open Spacestation-开源
04-27
总之，"Open Spacestation" 是一个充满活力的开源项目，体现了开放源代码社区的力量和创造力。无论是对游戏开发感兴趣，还是希望深度参与游戏的玩法设计，这个项目都提供了丰富的学习和贡献机会。通过下载 "openss-...
Baidu Apollo代码解析之Open Space Planner中的Hybrid A*
silver bullet
12-10 8201
大家好，我已经把优快云上的博客迁移到了知乎上，欢迎大家在知乎关注我的专栏慢慢悠悠小马车（https://zhuanlan.zhihu.com/c_1132958996826546176）。以后，我会把日常的思考放在优快云上，梳理过的精华文章放在知乎上，希望大家可以多多交流，互相学习。 目录 1. 节点的定义 2.Hybrid A*的规划主流程 3. 碰撞检测 4. ReedS...
精选资源
实践作业之openfoam实现边界速度扰动温度压力速度场分布求解.rar
06-28
通常，这会涉及到创建一个新的“用户定义”边界条件，这需要编写一个动态链接库，这个库包含了特定边界条件的实现代码。 动态链接库（DLL）是一种程序设计技术，它允许程序在运行时加载和卸载库，以节省内存并提高...
a*算法流程图(只是流程图)
12-19
a*算法流程图(只是流程图)A*算法是一种在静态路网中求解最短路径最有效的直接搜索方法，也是解决许多其他搜索问题的有效算法。算法中的距离估算值与实际值越接近，扩展的节点数越少， 搜索速度越快。
openFOAM代码阅读——基础代码中的char
qq_40583925的博客
06-11 1930
openFOAM的源码文件夹src中的内容如下： dyfluid@dyfluid:~/OpenFOAM/OpenFOAM-7/src$ ls Allwmake genericPatchFields rigidBodyDynamics atmosphericModels lagrangian rigidBodyMeshMotion combustionModels mesh rigidBodyState
百度Apollo5.0规划模块代码学习（五）开放空间回退决策分析
wwyklnh的博客
09-05 1640
代码分析如下： 加载配置文件， OpenSpaceFallbackDecider::OpenSpaceFallbackDecider(const TaskConfig& config) : Decider(config) {} 对于二次型公式：ax^2+bx+c=0，返回较小的解。非常正常的解法。 bool OpenSpaceFallbackDecider::Quardratic...
百度Apollo5.0规划模块代码学习（四）开放空间回退决策分析
wwyklnh的博客
09-05 1949
关于开发空间的相关介绍可以参考Apollo帮助文档：apollo/docs/specs/Open_Space_Planner.md。 简单来说，就是开放空间规划算法是针对倒车停车和急转弯开发的一种算法。 此算法接受来自两个不同来源的输入： -感知数据，包括但不限于障碍物； -通过高清地图获得的感兴趣区域（ROI）； 一旦数据就位，就会触发开放空间规划器。算法可以分为两步。 其算法结构如下图所示： ...
自动驾驶轨迹规划算法——Apollo OpenSpace Planner
swaggytiger的博客
08-14 1329
Apollo OpenSpace Planner是百度Apollo自动驾驶系统中专为非结构化道路设计的轨迹规划器。它直接在笛卡尔坐标系下进行空间搜索与轨迹优化，支持前进/倒车切换等复杂机动。核心流程包括：1) Hybrid A*算法在自由空间搜索可行路径；2) 轨迹平滑优化满足动力学约束；3) 时间参数化生成可执行轨迹。相比结构化道路规划器，它摆脱了车道线依赖，适用于自动泊车、狭窄调头、港口作业等低速场景。该算法通过状态空间离散化、混合启发式搜索、Reeds-Shepp分析连接等技术，在保证实时性的同时生成
Hybrd A*(混合A*)算法
热门推荐
u010241908的博客
03-09 2万+
Hybrid A*算法是一种图搜索算法，改进于A*算法。与普通的A*算法区别在于，Hybrid A*规划的路径考虑了车辆的运动学约束，即满足了车辆的最大曲率约束。
APOLLO混合A*算法详解
weixin_60232039的博客
02-03 5285
首先在这里介绍“节点”的概念，即Node3d类。//x,y,phi是node的坐标//step_size_是一段路径（如Reed-Shepp曲线）所包含的路径点数，而该node就是这段路径的终点//traversed_x,traversed_y,traversed_phi是node连接的一串点的坐标集合A*中的node单纯的指一个节点或一个状态，一般是其（x，y）坐标。这里的Node3d不同，除了包含一个点坐标（x_，y_，phi_）之外，还包含了一串这样的坐标集合。......
[规划算法]Hybrid A *算法原理
Forwarding3的博客
07-15 3295
hybrid A*算法原理
上述代码转换成python结合open3d实现
06-09
我们参考上述C++代码实现，将其转换为Python版本，并使用Open3D和numpy进行实现。由于Open3D本身不提供IRLS配准的直接接口，我们需要手动实现算法步骤。主要步骤：1.计算残差和代价2.基于残差计算权重（使用Huber核...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值