LQR横向控制联合仿真

一、准备工作

1：总质量等于悬架以上质量＋悬架质量✖2.即1270+88.6*2

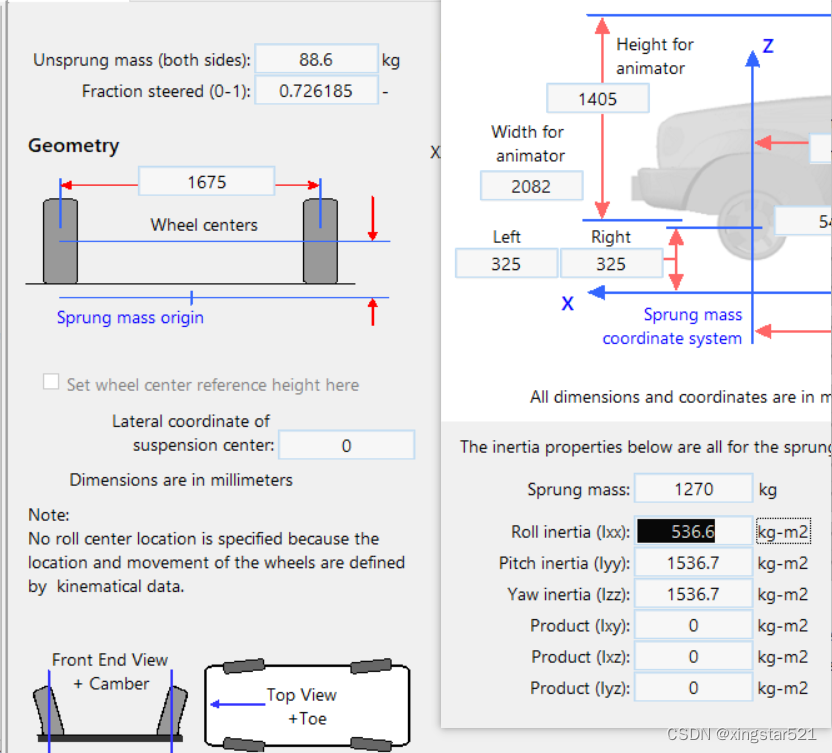
2：空气动力学-风阻关闭

 

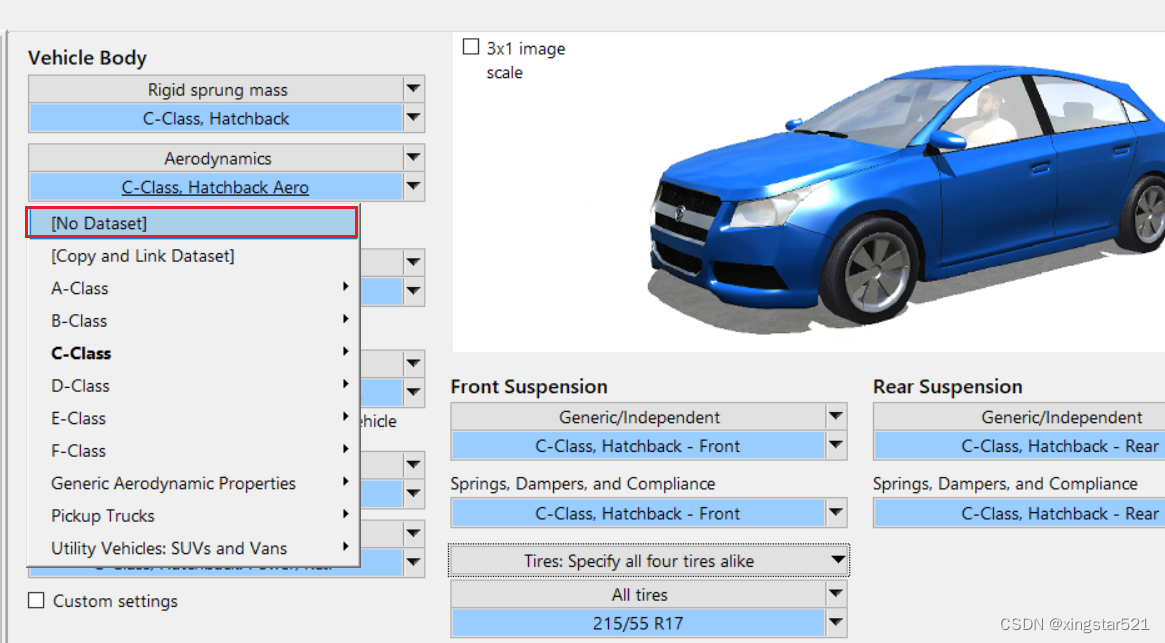
3：控制需要的量，状态量x,y,fa,vx,vy,fa_dot.  以及规划的 xr,yr,切线与x轴的夹角θr，曲率kr

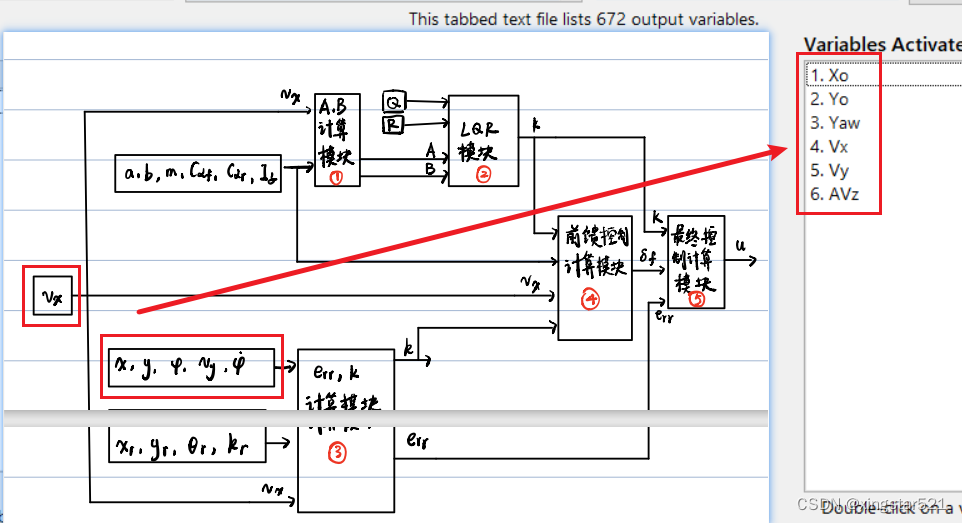
二、路径规划及路面设置

1：路径规划代码

routing_planning.m,由直线函数和圆弧函数组成。

运行前需要清空工作区

count=50;
[x1,y1,theta1,kr1]=straight([0,0],[20,0],0,count);
[x2,y2,theta2,kr2]=arc([20,0],[30,10],0,pi/2,count);
[x3,y3,theta3,kr3]=arc([30,10],[40,20],pi/2,0,count);
[x4,y4,theta4,kr4]=arc([40,20],[40,40],0,pi,count);
[x5,y5,theta5,kr5]=arc([40,40],[35,35],pi,3*pi/2,count);
[x6,y6,theta6,kr6]=arc([35,35],[25,35],3*pi/2,pi/2,count);
[x7,y7,theta7,kr7]=arc([25,35],[15,35],pi/2,3*pi/2,count);
[x8,y8,theta8,kr8]=arc([15,35],[5,35],3*pi/2,pi/2,count);
[x9,y9,theta9,kr9]=arc([5,35],[-15,35],pi/2,3*pi/2,count);
[x10,y10,theta10,kr10]=straight([-15,35],[-15,15],3*pi/2,count);
[x11,y11,theta11,kr11]=arc([-15,15],[0,0],3*pi/2,2*pi,count);
xr=[x1,x2,x3,x4,x5,x6,x7,x8,x9,x10,x11]