DL-IAPS & PJSO：路径和速度优化算法

1.算法介绍

虽然OBCA算法通过凸优化的强对偶性很好地解决了在开放空间和障碍物的无碰撞约束. 但是求解效率和鲁棒性较差, 单次求解时常可到1秒左右. 随着障碍物数量以及边数的增加, 会导致求解效率进一步降低甚至求不出解.

Apollo设计了一种纵横解耦的开放空间轨迹规划算法，将轨迹规划问题转换成路径规划DL-IAPS和速度规划PJSO两步完成。

DL-IAPS是一种分段的路径规划算法. OBCA是将整条路径一起进行平滑, DL-IAPS是将Hybird A*产生的粗糙的轨迹, 根据轨迹的前进/后退(倒车档)分成不同的段, 并且分段进行平滑. 同时保证规划后的路径不会和障碍物发生碰撞, 以及平滑后的路径满足曲率约束. 速度规划部分, 采用的是PJSO算法.

下图是Open Space算法框架 

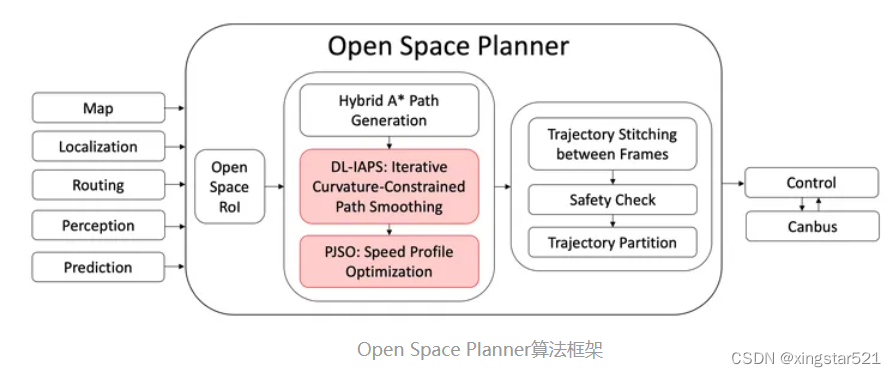
2.路径规划：DL-IAPS 

DL-IAPS全称：Dual Loop Iterative Anchoring Path Smoothing，双循环迭代锚点路径平滑算法。

算法流程：

        内层循环将粗糙的轨迹的轨迹作为参考路径，并利用曲率约束来平滑轨迹

        外层循环检查和障碍物是否有碰撞并通过收窄可行驶状态的区域

        当检查完所有障碍物是否与自车碰撞之后，外层循环终止

2.1.伪代码

伪代码： 

2.3.1.优化目标和约束条件 

约束条件：

起始点，末尾点位置约束：

                                            

起始点锚定：

                                      

末尾点锚定： 

                         

离散点的活动范围约束：

, for k=2, ...,n-3                                            

曲率约束：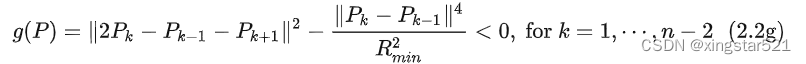 

2.3.2.SQP 

参考线平滑算法：

        1：参考线平滑算法一般来自地图的车道线，本身曲率较小

        2：参考线平滑点的数量较多，对实时性要求较高，所以不考虑曲率约束的二次规划方法进行求解 

开发空间算法：

        参考路径的曲率本身就是比较高的，必须把曲率约束加进去

由于非线性约束比如（2.2f)和（2.2g）导致2.2系列公式难以求解，故使用SQP方法来求解。

SQP将原问题近似转化为围绕当前迭代点的凸二次规划问题并不断求解直至收敛。 转化后的优化目标如(2.3a)所示, 第一项是相邻两个平滑度的代价, 第二项是曲率约束的松弛变量.

 

 

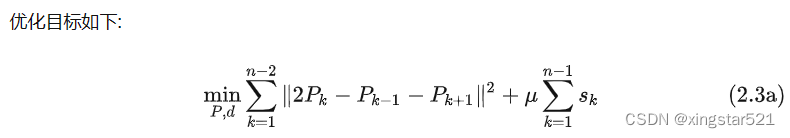
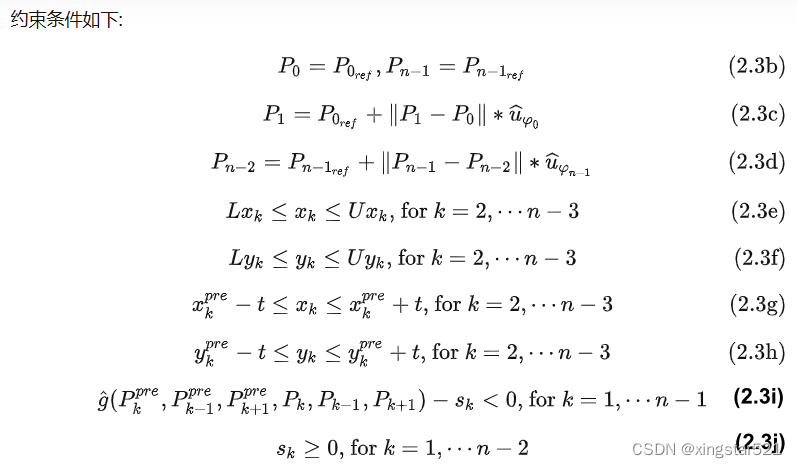
原公式(2.2f)转化成了(2.3e)和(2.3f), 即坐标要在给定的矩形框内, 矩形框的大小是在外层的Collision Check中进行更新的. 

• 在序列二次规划中, 可以采用上一次平滑的结果作为这一次的参考点. 同时对优化点增加一个可信区间约束(2.3g)和(2.3h), 从而避免上一次规划点和这一次的约束过远.
• 曲率约束(2.2g)通过欧拉法被转化成了(2.3i)的线性约束.
• (2.3j)是松弛变量的约束, 松弛变量要一直大于等于 0

2.4. 外层循环: 避免碰撞 

 在每一次平滑迭代之后, 会对所有的障碍物进行碰撞检查, 如果发生了碰撞, 则将发生碰撞的参考点调小圆形框的大小, 重新进行下一次的平滑, 不断迭代直到满足碰撞约束之后才结束.

如图 2.4 所示, 如果碰撞在第 个路径点被检测到, 则通过乘以一个小于 1 的系数 来收缩可行驶区域  .