皮尔森与斯皮尔曼相关系数：原理、步骤与公式解析

相关系数是衡量两个变量之间关联程度的重要统计工具，在数据分析、科学研究和商业决策中广泛应用。对于数据分析新手而言，理解皮尔森相关系数和斯皮尔曼秩相关系数的原理和应用场景至关重要。本文将通过生活化的例子、清晰的步骤分解以及直观的公式解释，帮助您掌握这两种相关系数的核心概念。

一、生活化例子理解两种相关系数的差异

1. 皮尔森相关系数的适用场景

皮尔森相关系数适合衡量两个变量之间的线性关系。让我们通过一个日常例子来理解：

假设您正在研究"身高"和"体重"之间的关系。收集了10位朋友的数据后，您发现身高和体重呈现明显的线性正相关——身高越高的人通常体重也越重。此时，使用皮尔森相关系数计算，结果可能是r=0.85，表明两者有较强的线性正相关关系。

另一个例子是"跑步速度"与"完成100米所需时间"之间的关系。显然，跑步速度越快，完成时间越短，呈现完美的线性负相关。皮尔森相关系数计算结果r=-1，表示完全的负线性相关 。

2. 斯皮尔曼秩相关系数的适用场景

斯皮尔曼相关系数适合衡量两个变量之间的单调关系，无论这种关系是线性的还是非线性的。让我们看一个典型的例子：

假设您研究"复习时间"和"考试成绩"之间的关系。收集了5位同学的数据后，发现随着复习时间的增加，考试成绩也提高，但这种关系并非线性的。比如，复习1小时可能提升10分，复习2小时再提升15分，复习3小时仅提升5分。此时，使用斯皮尔曼相关系数计算，结果可能是r_s=0.9，表明两者有很强的单调正相关关系；而皮尔森相关系数可能只有r=0.6，因为非线性关系导致线性相关性减弱。

另一个例子是"收入水平"与"幸福感"之间的关系。根据伊斯特林悖论，收入与幸福感在低收入阶段呈正相关，但达到一定水平后相关性减弱或消失。这种非线性但单调的关系在早期阶段适合用斯皮尔曼相关系数分析，而非皮尔森系数 。

二、两种相关系数的计算原理与步骤

1. 皮尔森相关系数的计算原理

皮尔森相关系数基于原始数据值，衡量两个变量之间的线性相关程度。计算步骤如下：

步骤一：计算两个变量的均值

先计算每个变量的平均值，作为后续计算的基础点。例如，对于身高和体重数据，分别计算平均身高和平均体重。

步骤二：计算每个数据点与均值的偏差

将每个数据点减去对应的均值，得到偏离平均值的程度。例如，某人身高比平均身高高5厘米，体重比平均体重重10公斤。

步骤三：计算协方差

协方差是衡量两个变量共同变化趋势的指标。计算方法是将每个数据点的偏差相乘后求平均。协方差越大，表示两个变量同步变化的趋势越强。

步骤四：计算标准差

标准差是衡量单个变量偏离均值程度的指标。计算每个变量的标准差，用于后续标准化。

步骤五：计算皮尔森相关系数

将协方差除以两个变量标准差的乘积，得到皮尔森相关系数。这个系数的范围在-1到1之间，绝对值越接近1，表示线性相关性越强。

2. 斯皮尔曼秩相关系数的计算原理。

斯皮尔曼相关系数基于数据的秩次（排名顺序），衡量两个变量之间的单调关系。

计算步骤如下：

步骤一：对两个变量的数据分别排序并赋予秩次

将每个变量的数据从小到大排序，赋予相应的排名（秩次）。例如，对于复习时间和考试成绩数据，分别将复习时间按长短排序，将成绩按高低排序。

步骤二：处理重复值

如果两个数据点的值相同，采用平均秩次的方法处理。例如，如果有两位同学复习时间都是2小时，那么他们的秩次应该是两个相邻秩次的平均值。

步骤三：计算每个数据点的秩次差

将同一数据点在两个变量中的秩次相减，得到秩次差( d_i )。例如，某位同学复习时间排名第3，成绩排名第2，那么秩次差是1。

步骤四：计算斯皮尔曼相关系数

使用秩次差计算斯皮尔曼相关系数。最常用的方法是使用秩差公式：

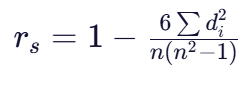
这个系数同样在-1到1之间，绝对值越接近1，表示单调相关性越强。三、公式的数学表达与直观解释

1. 皮尔森相关系数公式

数学表达式：

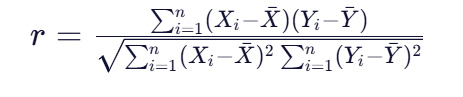
直观解释：

• 分子部分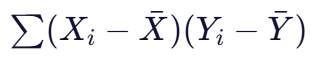： 是协方差的计算，表示两个变量共同变化的趋势。当两个变量都高于均值或都低于均值时，乘积为正，协方差增大；当一个变量高于均值而另一个低于均值时，乘积为负，协方差减小。
• 分母部分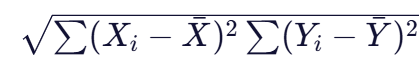： 是两个变量标准差的乘积，用于标准化协方差，消除量纲的影响。
• 整体结果：r的值在-1到1之间。当r=1时，表示完全正线性相关；当r=-1时，表示完全负线性相关；当r=0时，表示无线性相关关系。

2. 斯皮尔曼秩相关系数公式

斯皮尔曼秩相关系数有两种等价的计算方式：

方式一（秩差公式）：

直观解释：

• 核心思想：斯皮尔曼相关系数不关心变量的具体数值，只关注它们的排名顺序。即使变量之间是复杂的非线性关系，只要这种关系是单调的（即随着一个变量增加，另一个变量也增加或减少），斯皮尔曼相关系数就能准确捕捉到。
• 计算逻辑：通过将原始数据转换为秩次，消除了异常值和分布形态的影响，使计算更关注数据的相对位置而非绝对值。
• 结果解读：( r_s ) 的值同样在-1到1之间。当所有数据点的秩次差为0时（即两个变量的排名完全一致），( r_s=1 )；当排名完全相反时，( r_s=-1 )；当排名无相关性时，( r_s=0 )。

四、两种相关系数的应用场景对比

1. 皮尔森相关系数的适用条件

皮尔森相关系数适用于以下情况：

• 变量之间呈现线性关系
• 数据服从正态分布或接近正态分布
• 数据中没有明显的异常值
• 变量是连续型数据

例如，身高与体重的关系、温度与冰淇淋销量的关系等，通常适合使用皮尔森相关系数。

2. 斯皮尔曼秩相关系数的适用条件

斯皮尔曼相关系数适用于以下情况：

• 变量之间呈现非线性但单调的关系
• 数据分布未知或明显偏离正态分布
• 数据中存在异常值
• 变量是序数数据或需要非参数分析

例如，收入与幸福感的关系、考试成绩与复习时间的关系、基因表达量之间的关系等，通常适合使用斯皮尔曼相关系数。

五、总结与建议

1. 核心区别总结

特征	皮尔森相关系数	斯皮尔曼秩相关系数
基于数据	原始数值数据	秩次（排名顺序）数据
适用关系	线性关系	单调关系（线性或非线性）
对异常值敏感	敏感	不敏感
对分布要求	要求正态分布	无需特定分布
计算复杂度	中等	较高（需排序处理）

2. 实际应用建议

作为数据分析新手，您可以根据以下原则选择合适的相关系数：

首先，绘制变量之间的散点图，直观观察关系形态。如果呈现明显的直线趋势，优先考虑皮尔森相关系数；如果呈现曲线趋势但整体趋势一致（即单调关系），则选择斯皮尔曼相关系数。

其次，考虑数据的分布形态和异常值情况。如果数据明显偏离正态分布或存在异常值，斯皮尔曼相关系数通常更为稳健。

最后，理解相关系数不等于因果关系。即使两个变量之间存在高度相关，也不能直接推断因果关系，需要进一步的分析和验证。

通过掌握皮尔森相关系数和斯皮尔曼秩相关系数的原理和应用方法，您将能够更准确地分析变量之间的关系，为您的数据分析工作提供有力支持。