基于Canopy聚类的分块方法：从生活化例子到数学公式

Canopy分块方法是一种快速、高效的大数据预聚类技术，特别适合处理海量高维数据。它通过简单的距离计算和两个阈值参数，能够将数据集快速划分为多个可重叠的子集，这些子集被称为"Canopy"（树冠）。Canopy算法的核心价值在于：无需预先指定簇数k，通过"粗聚类"自动生成候选簇中心；仅需一次数据遍历，计算成本远低于K-means；作为预处理工具，为K-means提供初始k值和中心，提升其聚类效果 。这种方法虽然精度不如精确聚类算法，但其快速性和低计算成本使其成为大数据处理的重要预处理工具。

一、Canopy分块方法的生活化例子

超市商品分组的例子

想象一下你在一家大型超市工作，需要将货架上的商品按照相似性进行分组，以便后续进行更精细的分类或推荐。超市里有各种商品，比如牛奶、面包、薯片、洗发水、洗衣液、酸奶、饼干等。Canopy算法可以帮助你快速将这些商品初步分组。

首先，我们需要确定两个关键参数：T1和T2，其中T1 > T2。这里我们将T1设为10元，T2设为3元。这两个参数代表价格的相似程度阈值。

步骤1：随机选择一个商品作为第一个Canopy的中心

假设你随机选择了"牛奶"作为第一个Canopy的中心，此时这个Canopy的中心点就是牛奶的价格。

步骤2：计算其他商品与中心商品的价格距离

接下来，你需要计算其他所有商品的价格与牛奶价格的距离。例如：

• 面包：价格差2元
• 饼干：价格差4元
• 洗发水：价格差8元
• 酸奶：价格差1元
• 薯片：价格差5元
• 洗衣液：价格差12元

步骤3：根据阈值T1和T2进行分类

根据阈值T1=10元和T2=3元，将这些商品分为三类：

• 强标记（距离<T2）：面包（2元）、酸奶（1元）——这些商品与牛奶价格非常接近，将它们归入第一个Canopy，并且不再作为新的Canopy中心。
• 弱标记（T2≤距离<T1）：饼干（4元）、薯片（5元）——这些商品与牛奶价格有一定接近，将它们归入第一个Canopy，但它们仍然可以作为新的Canopy中心。
• 不属于当前Canopy（距离≥T1）：洗发水（8元）、洗衣液（12元）——这些商品与牛奶价格差异较大，不归入第一个Canopy，需要后续处理。

步骤4：移除强标记商品并重复步骤

此时，将面包和酸奶从待处理商品列表中移除，因为它们已经被确定属于第一个Canopy，并且不再作为新的Canopy中心。剩下的商品是饼干、薯片、洗发水、洗衣液。

步骤5：选择下一个商品作为新的Canopy中心

从剩下的商品中随机选择一个，比如洗发水。然后计算其他商品与洗发水的价格距离：

• 饼干：价格差4元
• 薯片：价格差3元
• 洗发水：价格差0元
• 洗衣液：价格差4元

步骤6：再次根据阈值分类

根据T1=10元和T2=3元：

• 强标记（距离<T2）：薯片（3元）——归入第二个Canopy（洗发水），并且不再作为新的Canopy中心。
• 弱标记（T2≤距离<T1）：饼干（4元）、洗衣液（4元）——归入第二个Canopy，但仍然可以作为新的Canopy中心。
• 不属于当前Canopy（距离≥T1）：无。

步骤7：移除强标记商品并继续处理

移除薯片后，剩下的商品是饼干、洗衣液。从这两个商品中随机选择一个，比如饼干，作为第三个Canopy的中心。

步骤8：计算剩余商品与新中心的距离

计算洗衣液与饼干的价格距离为4元，不小于T1=10元，因此洗衣液不归入第三个Canopy，形成第四个Canopy（洗衣液）。

最终结果：通过上述步骤，我们将原本需要逐一比较的商品快速分成了四个Canopy：

1. 第一个Canopy（牛奶）：包含牛奶、面包、酸奶、饼干、薯片
2. 第二个Canopy（洗发水）：包含洗发水、薯片、饼干
3. 第三个Canopy（饼干）：仅包含饼干
4. 第四个Canopy（洗衣液）：仅包含洗衣液

Canopy的特点：每个商品可能属于多个Canopy，例如饼干同时属于第一个Canopy（牛奶）和第二个Canopy（洗发水）。这种重叠的分组方式为后续的精确聚类（如K-means）提供了初始的簇中心和簇数，大大提高了后续聚类的效率。

二、Canopy算法的五个核心步骤

Canopy算法的实现可以归纳为五个核心步骤，这些步骤简单直观，但效果显著：

步骤1：初始化参数

• 设置两个距离阈值T1和T2，满足T1 > T2
• 选择合适的数据距离度量方法（如欧氏距离、余弦距离等）
• 将所有数据点放入待处理集合D中

步骤2：随机选择初始点

• 从待处理集合D中随机选取一个数据点p作为新Canopy的中心
• 将点p从集合D中移除

步骤3：计算距离并分配

• 遍历集合D中的剩余点q
• 计算点q与当前Canopy中心p的距离d
• 如果d < T1：将点q标记为"弱标记"，归入当前Canopy
• 如果d < T2：将点q标记为"强标记"，归入当前Canopy，并从集合D中移除
• 如果d ≥ T1：点q不归入当前Canopy，继续处理下一个点

步骤4：迭代处理剩余点

• 重复步骤2-3，直到待处理集合D为空
• 每次迭代都会生成新的Canopy中心，并减少集合D中的元素数量

步骤5：输出结果

• 生成所有Canopy的集合
• 每个Canopy包含中心点和归属的数据点
• 可以选择性地删除包含数据点数目较少的Canopy，以消除噪声和孤立点

Canopy算法的核心思想：通过快速、低成本的近似距离计算，将数据点快速划分为多个可重叠的子集。这种"粗聚类"方法虽然精度不如精确聚类算法，但其计算效率极高，特别适合处理大规模数据 。每个数据点可以属于多个Canopy，这种重叠的分组方式为后续的精确聚类提供了良好的初始条件。

三、Canopy算法的流程图和示意图解释

Canopy算法的流程图通常包含以下关键部分：

1. 输入部分：数据集D、距离阈值T1和T2（T1 > T2）、距离度量方法
2. 初始化部分：将所有数据点放入待处理集合D，设置计数器为0
3. 循环处理部分： 从D中随机选取一个点作为新的Canopy中心
   1. 计算剩余点到当前中心的距离
   2. 根据距离与T1、T2的关系进行分类
   3. 更新D集合（移除强标记点）
4. 终止条件：当D集合为空时，算法结束
5. 输出部分：所有生成的Canopy集合

示意图通常用两个同心圆来表示Canopy的覆盖范围，如图1所示：

          +-------------------+
          |       T1区域       |
          +-------------------+
                +-------------+
                |   T2区域     |
                +-------------+
                      中心点

图1：Canopy算法示意图

在这个示意图中：

• 实线圆的半径为T1，表示Canopy的覆盖范围
• 虚线圆的半径为T2，表示核心区域
• 位于T2区域内的点被视为强标记点，不再作为新的Canopy中心
• 位于T1和T2之间的点被视为弱标记点，属于当前Canopy但可以作为其他Canopy的中心
• 位于T1区域外的点不属于当前Canopy，需要后续处理

Canopy算法的流程图通常由以下几个主要模块组成：

1. 开始模块：算法的起点
2. 参数初始化模块：设置T1、T2和距离度量方法
3. 数据集初始化模块：将所有数据点放入待处理集合D
4. 循环处理模块： 从D中随机选取一个点
   1. 计算该点与所有现有Canopy中心的距离
   2. 根据距离与T1、T2的关系进行分类
   3. 更新D集合（移除强标记点）
5. 终止判断模块：检查D集合是否为空
6. 结果输出模块：输出所有Canopy及其中心点
7. 结束模块：算法的终点

Canopy算法的流程图特点：

• 单次遍历数据集即可完成聚类
• 每个数据点只需计算一次到Canopy中心的距离
• 无需预先指定聚类个数k
• 可以并行处理数据点，提高计算效率
• 生成的Canopy可以重叠，数据点可以属于多个Canopy

• Canopy算法的数学公式总结和解释

4. Canopy算法的数学表达

Canopy算法的完整数学表达可以归纳为以下过程：

1. 初始化：
   1. 设定阈值T1和T2（T1 > T2）
   2. 设定距离度量函数d()
   3. 将所有数据点放入集合D
2. 循环处理：
   1. 从D中随机选取一个点p
   2. 创建新的Canopy c，中心为p
   3. 对于D中的每个点q： 计算d(q, p)
      1. 如果d(q, p) < T1： 将q加入c
         1. 如果d(q, p) < T2： 将q从D中移除
   4. 重复直到D为空
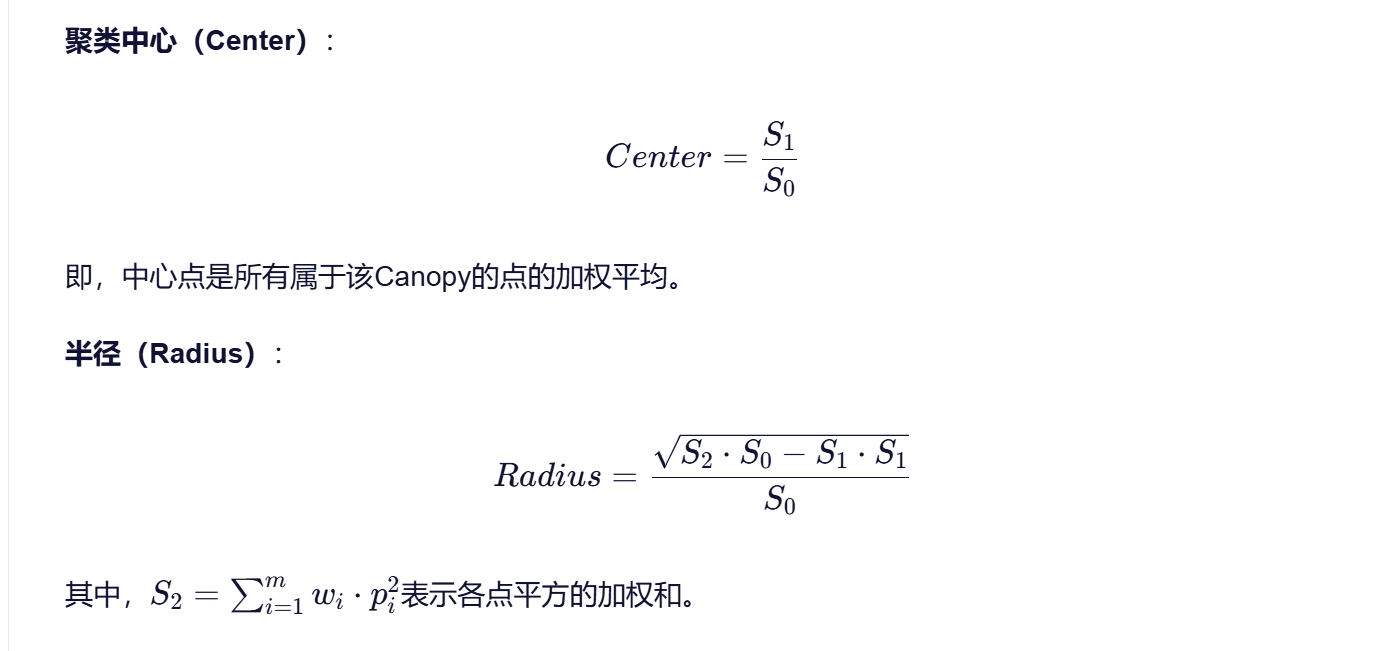
3. 可选的中心点更新：
   1. 对于每个Canopy c： 计算S0、S1、S2
      1. 更新中心Center = S1/S0
      2. 计算半径Radius = sqrt(S2S0 - S1S1)/S0

5. 参数选择的影响

Canopy算法的性能高度依赖于T1和T2的选择：

• T1过大：会导致Canopy覆盖范围过大，簇间重叠严重，无法有效区分簇
• T2过大：会快速删除大量点，导致Canopy数量过少（k值偏小）
• T2过小：会保留过多点，导致Canopy数量过多（k值偏大）

一般建议：T1和T2的取值可以通过数据采样或交叉验证确定。例如，可以计算数据点之间的平均距离，然后设置T1约为平均距离的2倍，T2约为平均距离的1倍。

五、Canopy算法的优缺点分析

优点

1. 计算效率高：Canopy算法仅需一次数据遍历，计算复杂度低，特别适合处理大规模数据
2. 无需预先指定k值：算法自动生成Canopy的数量，避免了K-means等算法需要预先指定k值的困难
3. 抗噪能力强：通过设置T2阈值，可以自动过滤掉孤立点和噪声点
4. 预处理效果好：为后续的精确聚类（如K-means）提供了良好的初始条件，减少了迭代次数
5. 实现简单：算法逻辑清晰，易于理解和实现

缺点

1. 精度较低：由于使用了近似距离计算和阈值判断，聚类结果可能不够精确
2. 阈值选择困难：T1和T2的取值对聚类结果影响较大，但缺乏通用的选择方法
3. 结果不稳定：随机选择初始点可能导致不同的聚类结果
4. 簇形状受限：算法假设簇是球形的，对复杂形状的簇可能效果不佳
5. 可扩展性有限：对于高维数据，距离计算可能变得困难，需要结合其他技术

Canopy算法的应用场景：Canopy算法特别适合作为K-means等精确聚类算法的预处理步骤，或者在需要快速聚类且对精度要求不高的场景中使用。例如，大规模用户行为分析、文本分类、图像处理等领域。

六、Canopy算法的改进和应用

改进方向

1. 中心点选择优化：原始Canopy算法随机选择初始点，可能导致中心点分布不均匀。改进方法包括：
   1. 选择距离数据均值点最近的点作为初始中心
   2. 采用最大权重乘积法选择初始中心
   3. 结合密度参数选择初始中心
2. 阈值自适应调整：改进算法可以根据数据分布动态调整T1和T2的值，例如：
   1. 通过计算数据点到均值点的最远距离L1和最近距离L2确定T1和T2
   2. 采用频率分布直方图类比出距离分布直方图，确定适宜的T1和T2值
3. 中心点更新机制：原始Canopy算法通常不更新中心点，改进版本可以计算更精确的中心点：
   1. 使用加权平均计算中心点（如公式Center = S1/S0）
   2. 结合其他距离度量方法更新中心点

应用案例

1. 电力企业流量数据分析：使用Canopy-K-means算法对电力系统日志数据进行聚类，提高了异常检测的效率和准确性
2. 社交电商平台用户行为分析：结合Canopy算法和K-means算法，对社交电商用户访问行为进行聚类，实现了更精准的用户分类
3. 角色挖掘：在访问控制系统中，使用Canopy预聚类提取子集交叠数据，减少谱聚类计算量，提高了角色挖掘的效率
4. 协同过滤推荐系统：将Canopy算法与K-means算法结合，用于协同过滤推荐系统中，解决了传统协同过滤算法对初始条件敏感的问题

Canopy算法的局限性：虽然Canopy算法在预处理阶段表现出色，但其精度较低，不能直接用于需要精确聚类的场景。通常需要结合K-means等精确聚类算法，才能获得高质量的聚类结果。

七、Canopy算法与K-means算法的结合应用

Canopy算法与K-means算法的结合是常见的应用方式，这种结合充分发挥了两种算法的优势：

1. 预处理阶段：使用Canopy算法对数据集进行快速粗聚类，生成初始的簇中心和簇数
2. 精确聚类阶段：使用K-means算法在Canopy的基础上进行精确聚类，得到最终的聚类结果

结合应用的优势：

• 避免了K-means算法对初始中心敏感的问题
• 减少了K-means算法的迭代次数，提高了计算效率
• 消除了数据集中的噪声点和孤立点，提高了聚类质量
• 可以处理大规模数据集，而无需预先指定k值

Canopy-K-means算法的流程：

1. 使用Canopy算法对数据集进行预处理，生成初始的簇中心和簇数
2. 将Canopy生成的簇中心作为K-means算法的初始中心
3. 使用K-means算法进行精确聚类，得到最终的聚类结果
4. 可以选择性地对Canopy进行合并或删除，优化聚类效果

Canopy算法的局限性：Canopy算法本身精度较低，不能直接用于需要精确聚类的场景。但通过与K-means等算法结合，可以充分发挥其预处理优势，提高整体聚类效率和质量。

八、总结与展望

Canopy分块方法作为一种快速、高效的预聚类技术，其核心思想是通过两个距离阈值将数据点划分为多个可重叠的子集。这种"粗聚类"方法虽然精度不如精确聚类算法，但其计算效率极高，特别适合处理大规模数据 。通过超市商品分组的例子，我们可以直观地理解Canopy算法的工作原理：根据价格相似性将商品快速分组，每个商品可能属于多个组，但最终通过后续算法得到精确分类。

Canopy算法的数学公式主要包括距离计算、阈值条件判断以及可选的中心点更新公式。算法的性能高度依赖于T1和T2的选择，这两个参数需要根据数据特性和应用场景进行合理设置 。虽然Canopy算法本身存在精度低、结果不稳定等局限性，但通过与K-means等精确聚类算法结合，可以充分发挥其预处理优势，提高整体聚类效率和质量。

未来，随着大数据技术的发展，Canopy算法可能会在以下方向进一步改进和应用：

• 结合深度学习技术，自动学习适宜的阈值T1和T2
• 开发更高效的并行实现，适应分布式计算环境
• 探索与其他聚类算法的结合方式，形成更强大的聚类框架
• 应用于更多新兴领域，如物联网数据分析、社交媒体用户行为分析等

对于数据挖掘和机器学习的新手来说，Canopy算法是一个很好的入门点，它简单直观，易于理解和实现，同时也能让你体验到聚类分析的基本思想和价值。通过掌握Canopy算法，你可以为进一步学习更复杂的聚类算法打下基础。