马氏距离：超越欧氏距离的智能距离度量

原创于 2025-12-22 17:32:40 发布 · 346 阅读

2 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #机器学习 #AI算法 #相似性算法 #马氏距离 #欧式距离

AI算法专栏收录该内容

16 篇文章

订阅专栏

马氏距离是一种在统计学和机器学习领域广泛应用的距离度量方法，由印度统计学家普拉桑塔·钱德拉·马哈拉诺比斯1936年提出。与传统的欧氏距离不同，马氏距离能够考虑数据点之间的相关性，并自动调整不同特征的尺度差异，使距离计算更加符合数据的实际分布特性。在处理多维数据时，马氏距离能够更准确地反映样本之间的相似程度，特别适用于需要考虑特征间关系的场景，如异常检测、分类任务和聚类分析等。

一、欧氏距离的局限性：身高体重的例子

让我们从一个简单的例子开始，理解为什么欧氏距离在某些情况下可能不够准确。假设我们有两个人的身高和体重数据，其中小明身高160cm，体重60kg；小王身高160cm，体重59kg；小李身高170cm，体重60kg。直观来看，小明和小王的身高相同，体重相差1kg，应该更相似；而小明和小李的体重相同，身高相差10cm，相似度可能较低。

但如果我们用欧氏距离来计算，结果却会有所不同。欧氏距离的计算公式为：

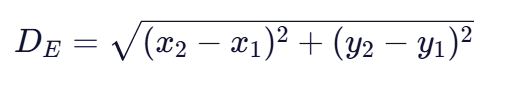
假设我们将身高和体重统一转换为厘米和克的单位，那么小明的数据为(160, 60000)，小王为(160, 59000)，小李为(170, 60000)。计算欧氏距离：

从欧氏距离的结果来看，小明和小李的距离仅为10，而小明和小王的距离却高达1000，这显然与我们的直观判断不符。问题出在欧氏距离没有考虑不同特征的尺度差异，体重以克为单位的数据变化范围远大于身高以厘米为单位的数据，导致体重的微小变化在欧氏距离中被过度放大。

此外，欧氏距离还忽略了特征之间的相关性。在现实生活中，身高和体重通常是正相关的，即身高较高的人往往体重也较重。这种相关性应该被考虑在距离计算中，但欧氏距离却完全忽略了这一点。

二、马氏距离的工作原理：消除量纲和相关性

马氏距离正是为了解决欧氏距离的这些问题而提出的。它通过两个关键步骤来消除量纲差异和特征相关性的影响：

第一步：标准化处理，消除量纲差异。马氏距离会根据每个特征的方差来调整该特征的权重，方差大的特征（如体重）会被赋予较小的权重，而方差小的特征（如身高）会被赋予较大的权重。这相当于将不同量纲的特征转换为同一量纲，使比较变得公平。

第二步：消除相关性影响，考虑特征间的关联。马氏距离通过协方差矩阵的逆矩阵来调整特征之间的相关性。例如，如果身高和体重高度相关，那么在计算距离时，它们的相关性会被"抵消"，避免重复计算。

这两个步骤使得马氏距离能够在多维空间中更准确地反映样本之间的相似程度，特别适合处理具有相关性和不同尺度的特征。

三、马氏距离的计算步骤详解

要计算马氏距离，需要遵循以下核心步骤：

计算均值向量：首先需要确定数据集的均值向量μ，即每个特征的平均值。例如，对于身高和体重两个特征，μ = [μ_身高, μ_体重]。
计算协方差矩阵：协方差矩阵Σ反映了特征之间的相关性和各自的方差。协方差矩阵的对角线元素是各特征的方差，非对角线元素是特征之间的协方差。
求协方差矩阵的逆矩阵：协方差矩阵的逆矩阵Σ⁻¹是消除相关性和调整尺度的关键。需要注意的是，协方差矩阵必须是可逆的，即数据集的样本数量必须大于特征数量，且特征之间不能完全共线。
计算样本与均值的差向量：对于任意一个样本点x，计算其与均值向量μ的差向量(x - μ) 。
矩阵运算：最后，进行矩阵运算得到马氏距离：

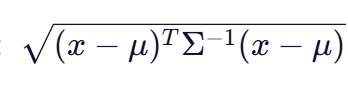
协方差矩阵的逆矩阵是马氏距离的核心，它不仅消除了特征之间的相关性，还根据各特征的方差进行了权重调整。这使得马氏距离能够在多维空间中更准确地反映样本之间的相似程度。

四、马氏距离的数学公式分解

马氏距离的数学公式为：

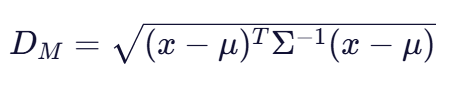
其中：

x 是待测样本点的特征向量
μ 是数据集的均值向量
Σ 是数据集的协方差矩阵
Σ⁻¹ 是协方差矩阵的逆矩阵
T 表示矩阵转置

我们可以将这个公式分解为几个关键部分：

1. 差向量(x - μ)：这部分计算样本点x与均值μ之间的差异，类似于欧氏距离中的差值计算。但与欧氏距离不同，马氏距离不仅计算差异，还会考虑这些差异的方向和重要性。

2. 协方差矩阵Σ⁻¹：这是马氏距离区别于欧氏距离的关键所在。协方差矩阵反映了数据的分布形状和特征之间的相关性。通过取逆矩阵Σ⁻¹，马氏距离能够：

消除特征之间的相关性
根据各特征的方差调整权重，消除量纲差异
将数据空间"拉伸"或"压缩"，使其变为各向同性的球形分布

3. 转置运算T：将差向量转置为行向量，以便与协方差矩阵的逆进行矩阵乘法运算。

4. 平方根运算：将结果开平方，使得距离的尺度与原始数据一致。

五、马氏距离与欧氏距离的对比分析

下表对比了马氏距离与欧氏距离的关键区别：

特性	欧氏距离	马氏距离
量纲影响	受量纲影响大，不同单位的特征权重不同	量纲无关，自动调整各特征权重
特征相关性	忽略特征之间的相关性	考虑特征之间的相关性
数据分布	假设各向同性分布，即各方向上数据分布相同	适应数据的实际分布形状
计算公式	$\sqrt{\sum_{i=1}^n (x_i - y_i)^2}$	$\sqrt{(x-μ)^T Σ^{-1} (x-μ)}$
适用场景	独立特征、相同量纲	相关特征、不同量纲

欧氏距离的局限性主要体现在两个方面：一是对不同量纲的特征赋予相同的权重，导致某些特征可能被过度强调；二是完全忽略特征之间的相关性，无法反映数据的真实分布特性。

马氏距离的优势在于：

能够消除量纲差异，使不同单位的特征具有可比性
考虑特征之间的相关性，反映数据的真实分布特性
根据各特征的方差自动调整权重，避免某些特征被过度强调
与χ²分布相关联，具有明确的统计意义

六、马氏距离的实际应用案例

让我们通过一个具体的二维数据集例子，来演示马氏距离如何考虑变量相关性和尺度差异。假设我们有一个数据集，包含两个特征：身高（cm）和体重（kg）。数据分布如下：

样本	身高	体重
样本1	160	60
样本2	165	65
样本3	170	70
样本4	175	75
样本5	180	80

计算均值向量μ和协方差矩阵Σ：

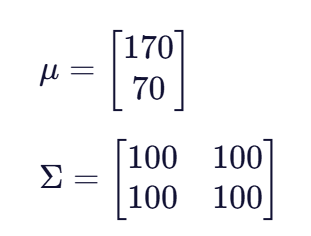
其中，身高方差为100（标准差为10），体重方差也为100（标准差为10），身高和体重的协方差为100，表明两者高度正相关。

现在计算样本1（160,60）到样本5（180,80）的欧氏距离和马氏距离：

欧氏距离：

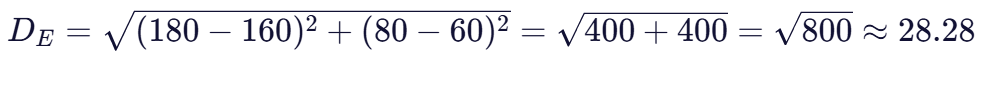
马氏距离：

首先计算协方差矩阵的逆：

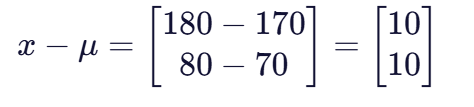
然后计算差向量：

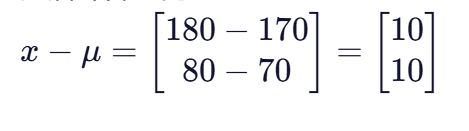
最后进行矩阵运算：

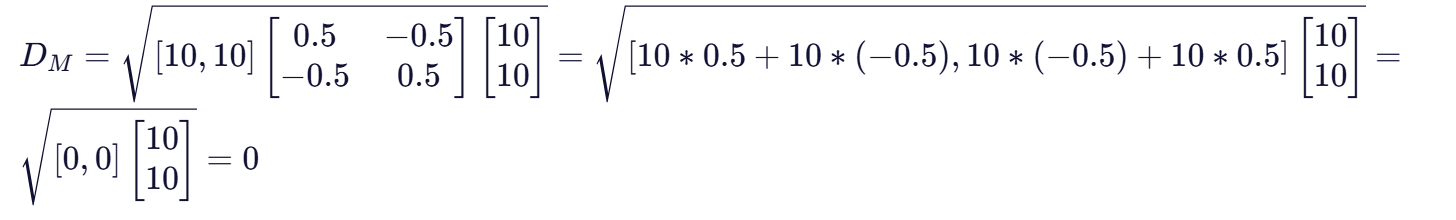这个结果表明，在马氏距离的视角下，样本1和样本5的距离为0，这与我们的直觉相符，因为它们在身高和体重上的变化方向完全一致，且变化幅度相同。而欧氏距离却给出了28.28的非零值，这主要是因为它没有考虑身高和体重之间的高度相关性。

七、马氏距离的实现代码示例

以下是使用Python计算马氏距离的代码示例：

import numpy as np
from scipy import linalg

# 创建示例数据集
data = np.array([
    [160, 60],
    [165, 65],
    [170, 70],
    [175, 75],
    [180, 80]
])

# 计算均值向量
mean = np.mean(data, axis=0)

# 计算协方差矩阵
cov = np.cov(data, rowvar=False)

# 计算协方差矩阵的逆
cov_inv = linalg.inv(cov)

# 定义马氏距离计算函数
def mahalanobis_distance(point, mean, cov_inv):
    diff = point - mean
    md = np.sqrt(np.dot(np.dot(diff.T, cov_inv), diff))
    return md

# 计算样本1到样本5的马氏距离
point1 = data[0]
point5 = data[4]
print("马氏距离:", mahalanobis_distance(point1, mean, cov_inv))  # 输出：0.0