Jaro-Winkler距离算法详解：从拼写纠错到相似度计算

Jaro-Winkler距离是一种衡量两个字符串相似程度的算法，特别适合处理短字符串如姓名、地址、产品型号等的相似性比较。该算法的核心思想是通过字符匹配、顺序分析和前缀加权三个维度综合评估字符串的相似性，返回0到1之间的值，值越接近1表示字符串越相似。与传统的编辑距离算法相比，Jaro-Winkler算法不仅考虑字符的匹配数量，还特别关注字符串开头部分的匹配，这对于处理拼写错误或名称变体特别有效。

一、直观理解：一个简单的拼写错误案例

让我们从一个常见的拼写错误案例入手，理解Jaro-Winkler算法的工作原理。假设我们有两个字符串：“Color”（正确拼写）和"Colouer"（拼写错误）。这两个词在英语中都是指"颜色"，但由于拼写错误，需要算法来判断它们的相似度。

第一步：确定匹配窗口

对于长度为5的"Color"和长度为6的"Colouer"，匹配窗口大小计算为：

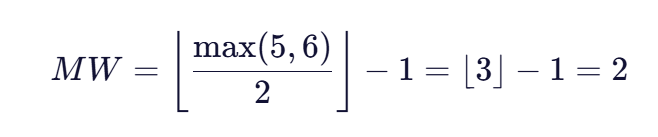
这意味着每个字符在另一个字符串中的匹配位置最多可以偏离当前字符位置2个位置。第二步：确定匹配字符

遍历每个字符，在匹配窗口范围内寻找匹配：

字符串位置	Color字符	Colouer字符	匹配情况
0	C	C	匹配
1	O	O	匹配
2	L	L	匹配
3	O	O	匹配
4	R	E	不匹配

虽然"Color"的最后一个字符R与"Colouer"的E不匹配，但"Colouer"的最后一个字符R在"Color"中位置4，超出窗口范围（窗口为2）。因此，匹配字符数m为4，而非5。

第三步：计算换位数

将两个字符串的匹配字符按原始顺序排列：

• Color的匹配字符顺序：C(0), O(1), L(2), O(3), R(4)
• Colouer的匹配字符顺序：C(0), O(1), L(2), O(3), R(5)

对比两个字符串的匹配字符顺序，发现R在两个字符串中的位置都是第4个字符（在Color中是位置4，在Colouer中是位置5），顺序一致，因此换位数t为0。

第四步：计算Jaro相似度

代入Jaro相似度公式：

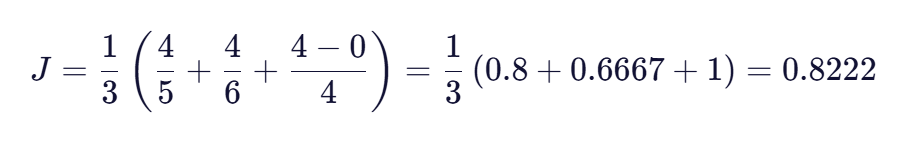
]第五步：应用前缀加权

检查两个字符串的前缀匹配情况，发现前4个字符"COLO"完全匹配，因此前缀长度L=4。代入Jaro-Winkler公式：

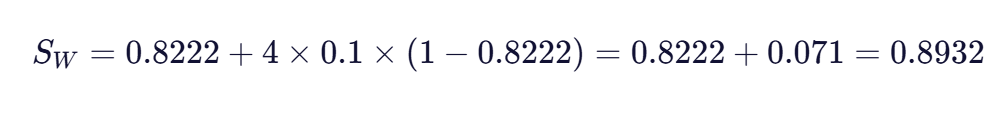
最终结果：两个字符串的Jaro-Winkler相似度为0.8932，接近0.9，表明它们高度相似。

二、算法原理步骤详解

Jaro-Winkler算法可以拆解为四个核心步骤，每个步骤都关注字符串相似性的一个关键维度：

步骤1：计算匹配窗口

匹配窗口是算法中用于限定字符匹配范围的关键参数。对于两个字符串s1和s2，匹配窗口大小计算为：

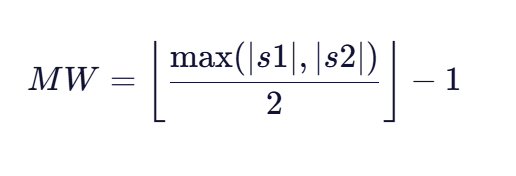
这个窗口决定了字符在两个字符串中的位置距离不超过MW时才可能被视为匹配。例如，对于长度为7的字符串，匹配窗口为2（floor(7/2)-1=3-1=2）。这意味着每个字符只能在另一个字符串中±2的位置范围内寻找匹配，超过这个范围即使字符相同也不会被判定为匹配。

步骤2：确定匹配字符

遍历两个字符串的每个字符，寻找在匹配窗口范围内的相同字符。需要注意的是，每个字符只能匹配一次，避免重复计数。

具体操作如下：

1. 初始化两个标记数组，记录哪些字符已经被匹配
2. 对于s1中的每个字符，从其位置±MW范围内在s2中寻找未被匹配的相同字符
3. 对于s2中的每个字符，同样从其位置±MW范围内在s1中寻找未被匹配的相同字符
4. 记录匹配的字符总数m

匹配字符的确定是算法的基础，它反映了两个字符串在字符构成上的相似程度。例如，在"Color"和"Colouer"的案例中，匹配字符数m为4，因为R在两个字符串中的位置超出匹配窗口范围。

步骤3：计算换位数目

换位数目t反映了匹配字符在两个字符串中的顺序差异。计算方法如下：

1. 将两个字符串的匹配字符按原始顺序排列
2. 统计在两个排列后的字符序列中，位置不一致的字符对数t’
3. 换位数目t计算为：

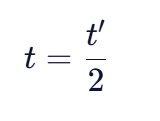
换位数目的计算考虑了字符顺序的影响。例如，"MARTHA"与"MARHTA"的匹配字符数m=6，但T和H的位置在两个字符串中颠倒，因此t’=2，换位数t=1。这表明虽然字符完全匹配，但顺序存在差异。

步骤4：计算Jaro-Winkler相似度

在Jaro相似度的基础上，Jaro-Winkler算法引入了前缀加权因子，特别重视字符串开头部分的匹配。计算公式为：

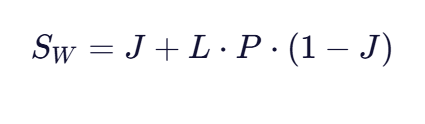
其中：

• J是Jaro相似度
• L是两个字符串共同前缀的长度（最大不超过4）
• P是前缀权重因子（默认值为0.1，最大不超过0.25）

前缀加权是Jaro-Winkler算法的创新点，它解决了Jaro算法在处理开头部分相似但后续部分差异较大字符串时的不足。例如，"DwAyNE"和"DuANE"的Jaro相似度可能较低，但通过前缀加权，可以提高它们的相似度评分，因为开头部分"D"和"u"的差异可能只是拼写错误。

三、Jaro-Winkler算法数学公式详解

Jaro-Winkler算法包含两个核心公式：Jaro相似度公式和Jaro-Winkler调整公式。

1. Jaro相似度公式

Jaro相似度衡量两个字符串在字符匹配和顺序上的相似程度：

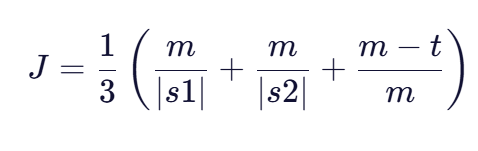
公式中的参数解释：

• ( m )：两个字符串之间的匹配字符数（需去重且在匹配窗口内）
• ( |s1| )、( |s2| )：两个字符串的长度
• ( t )：换位数，即需要交换位置的字符对数（计算方法见下文）

Jaro相似度的三个组成部分分别衡量：

这三个比例取平均值，形成最终的Jaro相似度J。

2. 换位数计算公式

换位数t的计算基于匹配字符的顺序差异：

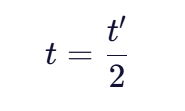
其中：

• ( t’ )：匹配字符中顺序不一致的字符对数

3. Jaro-Winkler调整公式

在Jaro相似度基础上，Jaro-Winkler算法引入了前缀加权：

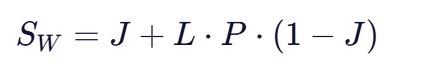
其中：

• ( SW )：最终的Jaro-Winkler相似度
• ( L )：两个字符串共同前缀的长度（最大不超过4）
• ( P )：前缀权重因子（默认值为0.1，最大不超过0.25）

参数范围说明：

• ( L )的取值范围为0到4，超过4的部分不计入前缀加权
• ( P )的取值范围为0到0.25，通常设为0.1。若超过0.25，可能导致( S_W >1 )，失去相似度评分的意义

四、算法特点与应用场景

Jaro-Winkler算法的特点：

1. 短字符串优化：特别适合处理长度较短的字符串（如人名、地名、产品型号等），对于长字符串的相似度计算效果可能不佳
2. 前缀敏感：对字符串开头部分的匹配给予额外权重，这对于处理拼写错误特别有效
3. 顺序敏感：不仅考虑字符匹配，还考虑字符顺序，能够区分如"ABCD"和"DCBA"这样的字符串
4. 计算高效：相比一些复杂的文本相似度算法，Jaro-Winkler计算速度较快，适合大规模数据处理

Jaro-Winkler算法的应用场景：

1. 数据清洗：在数据库中识别重复记录，如客户信息表中"张伟"和"张为"这样的近似姓名
2. 拼写纠错：搜索引擎或输入法中，为用户提供拼写错误的自动纠正
3. 地址匹配：物流系统中匹配相似的地址，如"北京市海淀区中关村大街"和"北京海淀中关村大街"
4. 实体识别：在自然语言处理中，识别文本中指代同一实体的不同名称

五、算法实现与优化

Jaro-Winkler算法的实现要点：

1. 字符处理：通常将字符串统一转换为小写，忽略大小写差异
2. 去重机制：每个字符只能匹配一次，避免重复计数
3. 边界条件：当m=0时，相似度直接为0，无需计算后续步骤
4. 结果限制：最终相似度( SW )不应超过1，若超过则取1

算法优化方向：

1. 前缀长度调整：根据具体应用场景，可以调整最大前缀长度（如从默认的4调整为2或3）
2. 权重因子调整：根据需求调整前缀权重因子P（如从0.1调整为0.15）
3. 匹配窗口调整：对于某些特殊场景，可以调整匹配窗口的计算方式
4. 多语言支持：针对不同语言特性（如中文、阿拉伯语等），调整字符匹配规则

Jaro-Winkler算法的局限性：

1. 无法处理插入/删除操作：与Levenshtein编辑距离不同，Jaro-Winkler不直接考虑插入或删除字符的操作
2. 对长字符串效果有限：随着字符串长度增加，匹配窗口也会增大，可能导致算法对长字符串的相似度判断不够准确
3. 参数依赖性强：算法结果高度依赖匹配窗口、前缀长度和权重因子的设置，需要根据具体应用场景进行调整

六、与其他相似度算法的比较

将Jaro-Winkler算法与几种常见的字符串相似度算法进行比较，可以更清晰地理解其特点和适用场景：

算法	适用场景	优点	缺点
Jaro-Winkler	短字符串（如人名、地址）	前缀敏感，计算高效	无法处理插入/删除，对长字符串效果有限
Levenshtein	各类字符串	考虑插入/删除/替换操作	计算复杂度高（O(nm)）
LCS（最长公共子序列）	语义相似度分析	考虑子序列匹配	忽略字符顺序，对顺序敏感度不足
余弦相似度	长文本相似度分析	适合高维向量空间	需要向量化处理，计算复杂

Jaro-Winkler算法与Levenshtein算法的主要区别在于：Levenshtein算法关注将一个字符串转换为另一个字符串所需的最少编辑操作次数（插入、删除、替换），而Jaro-Winkler算法则关注字符匹配、顺序和前缀的相似性。对于短字符串的相似性判断，Jaro-Winkler通常比Levenshtein算法更准确，因为它能够捕捉到字符顺序和前缀匹配的重要性 。

七、总结与实际应用建议

Jaro-Winkler算法的核心价值在于它能够高效地衡量两个短字符串的相似程度，特别适合处理拼写错误和名称变体 。通过匹配窗口限定字符匹配范围，确保算法不会被远距离字符干扰；通过换位数计算反映字符顺序的影响，避免简单匹配导致的误判；通过前缀加权特别重视字符串开头部分的匹配，这对于处理人名、地名等实际应用尤为重要。

在实际应用中，建议根据具体场景调整算法参数：

• 对于对前缀匹配要求较高的场景（如姓名匹配），可以适当增加P的值（但不超过0.25）
• 对于对顺序匹配要求较高的场景（如产品型号匹配），可以更加关注换位数t的计算
• 对于长字符串的相似度判断，可以考虑与其他算法（如Levenshtein或余弦相似度）结合使用

Jaro-Winkler算法作为一种简单而有效的字符串相似度计算方法，在数据清洗、拼写纠错和实体识别等领域具有广泛的应用前景。通过理解其原理和参数含义，可以更好地应用于实际项目中，提高数据处理的准确性和效率。