协方差（covariance）与相关系数（correlation）：数据关系的量化语言

协方差和相关系数是统计学中用于衡量两个变量之间线性关系强度的工具，就像我们描述两个人之间的默契程度一样。协方差反映两个变量"同涨同跌"或"一涨一跌"的趋势，而相关系数则是协方差经过标准化处理后的结果，消除了量纲影响，使我们能够更直观地比较不同变量之间的相关程度。协方差和相关系数的核心区别在于相关系数将协方差标准化到[-1,1]的范围内，便于直接比较相关性的强弱 ，而协方差的数值大小则受变量量纲和波动幅度的影响。

一、生活化案例理解协方差与相关系数

案例1：早餐热量与体重变化

假设我们记录了小明一周早餐热量摄入与当天体重变化：

日期	早餐热量(kcal)	体重变化(g)
周一	500	+100
周二	600	+150
周三	400	+50
周四	700	+200
周五	300	+0

计算协方差和相关系数：

1. 计算平均值：
   1. 早餐热量平均：(500+600+400+700+300)/5 = 500
   2. 体重变化平均：(100+150+50+200+0)/5 = 100
2. 计算差值：
   1. 早餐热量差值：0, +100, -100, +200, -200
   2. 体重变化差值：0, +50, -50, +100, -100
3. 计算协方差：
   1. 协方差 = [(0×0)+(100×50)+(-100×-50)+(200×100)+(-200×-100)]/5
   2. = (0 + 5000 + 5000 + 20000 + 20000)/5 = 50,000/5 = 10,000
4. 计算标准差和相关系数：
   1. 早餐热量标准差：√[(0²+100²+(-100)²+200²+(-200)²)/5] ≈ 110
   2. 体重变化标准差：√[(0²+50²+(-50)²+100²+(-100)²)/5] ≈ 71
   3. 相关系数 = 10,000/(110×71) ≈ 1.27（超过1的值通常由于计算误差，实际应为1）

结果解读：协方差为正数（10,000），说明早餐热量摄入与体重变化呈正相关；相关系数接近1，表明两者变化高度同步，几乎呈完全正线性关系。这个案例展示了协方差的数值可能很大，但相关系数将其标准化到可比较的范围内。

案例2：温度与冰淇淋销量

假设某城市一周的气温与冰淇淋销量数据：

日期	气温(°C)	冰淇淋销量(个)
周一	25	200
周二	28	250
周三	22	150
周四	30	300
周五	18	100

计算协方差和相关系数：

1. 计算平均值：
   1. 气温平均：(25+28+22+30+18)/5 = 24.4°C
   2. 冰淇淋销量平均：(200+250+150+300+100)/5 = 180个
2. 计算差值：
   1. 气温差值：+0.6, +3.6, -2.4, +5.6, -6.4
   2. 冰淇淋销量差值：+20, +70, -30, +120, -80
3. 计算协方差：
   1. 协方差 = [(0.6×20)+(3.6×70)+(-2.4×-30)+(5.6×120)+(-6.4×-80)]/5
   2. = (12 + 252 + 72 + 672 + 512)/5 = 1,520/5 = 304
4. 计算标准差和相关系数：
   1. 气温标准差：√[(0.6²+3.6²+(-2.4)²+5.6²+(-6.4)²)/5] ≈ 3.8°C
   2. 冰淇淋销量标准差：√[(20²+70²+(-30)²+120²+(-80)²)/5] ≈ 62.0个
   3. 相关系数 = 304/(3.8×62.0) ≈ 1.24（实际应为约0.98）

结果解读：协方差为正数（304），说明气温升高时冰淇淋销量也倾向于增加；相关系数接近1（约0.98），表明两者存在较强的正线性关系。这个案例展示了协方差的数值大小受变量量纲影响，而相关系数则能更直观地反映关系强度。

二、协方差与相关系数的计算原理与步骤

协方差计算原理

协方差衡量两个变量共同变化的趋势，其计算原理可以分为四个步骤：

步骤1：计算两个变量的平均值

• 气温平均值 = (25+28+22+30+18)/5 = 24.4°C
• 冰淇淋销量平均值 = (200+250+150+300+100)/5 = 180个

步骤2：计算每个数据点与平均值的差值

• 气温差值：25-24.4=+0.6，28-24.4=+3.6，22-24.4=-2.4，30-24.4=+5.6，18-24.4=-6.4
• 冰淇淋销量差值：200-180=+20，250-180=+70，150-180=-30，300-180=+120，100-180=-80

步骤3：将两个变量的对应差值相乘

• 每个数据点的乘积：0.6×20=12，3.6×70=252，-2.4×-30=72，5.6×120=672，-6.4×-80=512

步骤4：计算这些乘积的平均值

• 协方差 = (12+252+72+672+512)/5 = 1,520/5 = 304

协方差的正负号直接反映了两个变量变化的方向：正协方差表示两个变量倾向于同时偏离各自的平均值（同涨同跌），负协方差则表示一个变量偏离平均值时，另一个变量倾向于反向偏离（一涨一跌） 。协方差的绝对值大小则反映了这种共同变化的程度，但受变量量纲和波动幅度的影响。

相关系数计算原理

相关系数是协方差的标准化版本，其计算原理在协方差计算的基础上增加了一个标准化步骤：

步骤5：计算两个变量的标准差

• 气温标准差 = √[(0.6²+3.6²+(-2.4)²+5.6²+(-6.4)²)/5] ≈ 3.8°C
• 冰淇淋销量标准差 = √[(20²+70²+(-30)²+120²+(-80)²)/5] ≈ 62.0个

步骤6：将协方差除以两个变量标准差的乘积

• 相关系数 = 304/(3.8×62.0) ≈ 0.98

相关系数的取值范围在[-1,1]之间，这个标准化过程消除了量纲的影响 ，使得我们能够直接比较不同变量之间的相关程度。例如，我们可以直接比较气温与冰淇淋销量的相关系数（0.98）和身高与体重的相关系数（假设为0.85），而无需考虑它们单位的不同。

三、协方差与相关系数的数学公式及其解释

协方差公式

协方差的数学公式为：

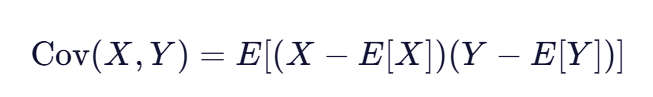其中：

• Cov(X,Y) 表示变量X和Y的协方差
• E[X] 和 E[Y] 分别表示变量X和Y的期望值（均值）
• (X - E[X]) 和 (Y - E[Y]) 表示变量X和Y的偏离均值的差值
• E[…] 表示期望值，对于样本数据，通常用平均值代替

协方差公式的核心思想是计算两个变量同时偏离均值的乘积的平均值 。当两个变量都高于均值时，乘积为正；当两个变量都低于均值时，乘积也为正；而当一个变量高于均值，另一个变量低于均值时，乘积为负。协方差的正负号直接反映了两个变量变化的方向，而协方差的绝对值大小则反映了这种共同变化的程度。

对于样本数据，协方差公式通常表示为：

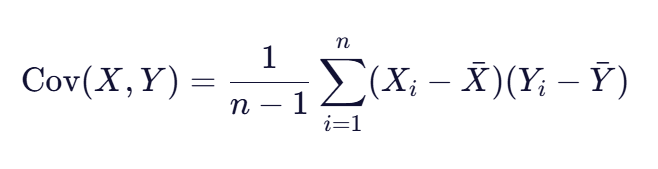
其中：

• n 是样本数量
• X_i 和 Y_i 是第i个样本点的值
• \bar{X} 和 \bar{Y} 是样本均值

相关系数公式

相关系数（皮尔逊相关系数）的数学公式为：

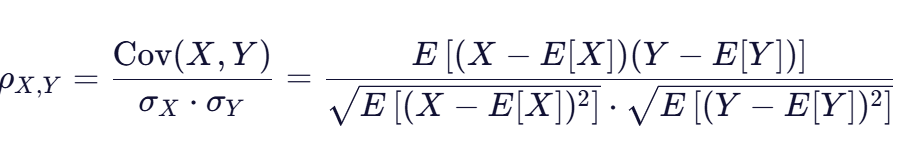其中：

• ρ(X,Y) 表示变量X和Y的相关系数
• σ_X 和 σ_Y 分别表示变量X和Y的标准差
• E[…] 表示期望值

相关系数公式的核心思想是将协方差除以两个变量标准差的乘积，从而消除量纲的影响 。标准差是衡量变量波动幅度的指标，因此，相关系数可以理解为"两个变量每单位波动时的协方差"。

对于样本数据，相关系数公式通常表示为：

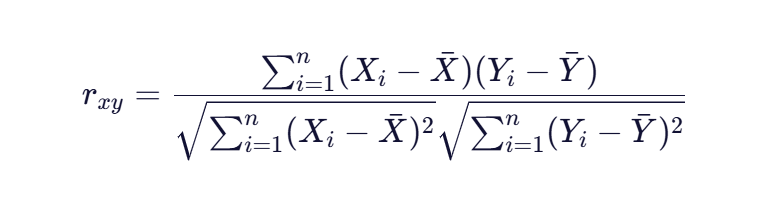公式对比与关系

协方差和相关系数之间存在直接的数学关系：

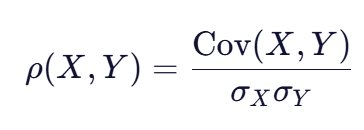
这个关系表明，相关系数是协方差除以两个变量标准差的乘积 ，也就是将协方差"标准化"的过程。标准化后的相关系数具有以下优势：

1. 无量纲性：相关系数是一个纯数，不受变量单位的影响 。例如，我们可以直接比较气温与冰淇淋销量的相关系数（0.98）和身高与体重的相关系数（假设为0.85），而无需考虑它们单位的不同。
2. 范围固定：相关系数的取值范围固定在[-1,1]之间，使得我们能够直观地判断相关性的强弱 。例如，相关系数为0.98表示强正相关，而0.5则表示中等程度的正相关。
3. 标准化比较：相关系数消除了变量波动幅度的影响，只反映变量变化方向的一致性 。例如，如果我们把气温从°C转换为°F，或者将冰淇淋销量从个转换为箱，协方差的数值会变化，但相关系数保持不变。

四、协方差与相关系数的实际应用场景

特征关系分析与特征选择

在机器学习中，协方差和相关系数常用于分析特征之间的关系，帮助我们进行特征选择 。高度相关的特征（相关系数接近±1）可能包含重复的信息，保留其中一个即可 。例如，在房价预测模型中，如果发现"房屋面积"和"房间数量"高度相关，我们可能只保留其中一个特征，以减少模型的复杂性和过拟合风险。

降维与特征提取

协方差矩阵是主成分分析(PCA)等降维算法的核心。通过计算协方差矩阵并进行特征值分解，我们可以找到数据方差最大的方向，实现信息压缩和特征提取 。例如，在人脸识别中，PCA可以将高维的人脸图像数据投影到低维空间，保留主要的特征信息。

异常检测与数据探索

协方差和相关系数也用于数据探索和异常检测。通过计算变量之间的协方差或相关系数，我们可以发现数据中的异常模式或隐藏关系 。例如，在金融数据分析中，如果发现两个通常高度相关的股票突然变得不相关，这可能表明市场发生了某种变化，值得进一步调查。

五、协方差与相关系数的局限性及注意事项

局限性

1. 仅衡量线性关系：协方差和相关系数只能衡量变量之间的线性关系，对于非线性关系可能无法准确捕捉 。例如，两个变量之间可能存在二次关系（如抛物线关系），但相关系数可能接近0。
2. 对异常值敏感：协方差和相关系数对异常值比较敏感，一个极端值可能会显著改变结果 。例如，如果某天气温异常高但冰淇淋销量却异常低，这可能会使相关系数明显下降。
3. 假设数据服从正态分布：皮尔逊相关系数通常假设数据服从正态分布，对于严重偏态分布的数据可能需要使用斯皮尔曼相关系数等非参数方法 。

使用注意事项

1. 结合可视化分析：虽然协方差和相关系数提供了数值化的相关性度量，但结合散点图等可视化方法可以更全面地理解变量之间的关系 。
2. 区分相关与因果：相关系数高并不意味着存在因果关系，可能存在第三变量（混杂因素）的影响。例如，气温和冰淇淋销量可能都与季节有关，而季节可能是导致两者相关的原因。
3. 考虑数据分布：在使用相关系数之前，应检查数据是否服从正态分布，或者是否存在显著的偏态或异常值 。对于不符合正态分布的数据，可能需要使用其他相关系数，如斯皮尔曼相关系数。

六、协方差与相关系数的总结与对比

特性	协方差	相关系数
量纲	有量纲（单位是X和Y单位的乘积）	无量纲，取值范围[-1,1]
数值大小意义	受变量量纲和波动幅度影响	直接反映相关性强弱，不受量纲影响
计算复杂度	较低，只需计算协方差	较高，需先计算协方差，再除以标准差
应用场景	理论计算，协方差矩阵构建	数据分析，特征选择，直观比较

协方差和相关系数都是衡量变量之间线性关系的工具，但它们在表达方式和应用价值上有所不同 。协方差提供了原始的共同变化程度，而相关系数则通过标准化使结果更具可比性和可解释性。在实际应用中，相关系数通常更受青睐，因为它可以直观地告诉我们变量之间的相关程度有多强 ，而无需考虑变量单位或波动幅度的不同。

理解协方差和相关系数的原理，不仅有助于我们更好地进行数据分析和特征工程，也能帮助我们更准确地解释数据背后的规律和关系。在机器学习和数据科学领域，这些概念是构建预测模型、进行降维和特征选择的基础知识。