欧氏距离相似算法：两点之间的直线距离

一、核心概念：什么是欧氏距离？

欧氏距离相似算法是一种基于几何距离概念的相似性度量方法，它通过计算两个向量在多维空间中的直线距离来判断它们的相似程度。距离越小，表示两个样本越接近，也越相似；距离越大，则表示两者差异越大，相似度越低。这种方法直观易懂，计算简单，是数据分析和机器学习中最常用的相似度度量方法之一。

简单来说，它就是 “两点之间的直线距离”。

二、数学定义与公式

欧氏距离的计算基于勾股定理。根据空间维度的不同，公式略有扩展。

四、应用场景

欧氏距离因其直观性，在众多领域有广泛应用：

1. 机器学习和数据挖掘
   1. K-最近邻算法（K-NN）：用于分类或回归，通过计算待分类样本与所有训练样本的欧氏距离，找出最近的K个“邻居”，根据这些邻居的类别进行投票。
   2. K-均值聚类（K-Means）：通过计算数据点到簇中心（质心）的欧氏距离，来将数据点分配到最近的簇。
   3. 主成分分析（PCA）：在降维后，通常使用欧氏距离来衡量数据点之间的相似性。
2. 计算机视觉
   1. 图像识别：将图像表示为像素值的向量后，可以通过计算欧氏距离来比较两张图像的相似度。
   2. 特征匹配：在图像中提取的特征点（如SIFT, ORB）可以用描述子向量表示，通过欧氏距离可以找到两幅图像中相似的特征点。
3. 推荐系统
   1. 可以将用户或物品表示为特征空间中的点，通过计算用户/物品之间的欧氏距离来衡量其相似性，从而进行推荐。
4. 地理信息系统（GIS）
   1. 计算地图上两个坐标点之间的实际直线距离。

五、优点与局限性

优点：

• 直观易懂：符合人类对空间距离的直观感受。
• 计算简单：公式直接，易于实现和计算。

局限性：

• 对量纲敏感：如果不同特征的量纲（单位）不同，例如身高（米）和体重（公斤），数值范围大的特征（如体重）会主导距离的计算结果。解决方案：需要进行数据标准化（如Z-score标准化）。
• 对异常值敏感：由于计算中包含了平方项，某个维度上的巨大差异会对整体距离产生非常大的影响。
• 高维空间中的问题（“维度灾难”）：在非常高维的空间中，所有点对之间的欧氏距离可能变得非常接近，这使得距离区分度下降，影响一些依赖距离的算法（如K-NN）的性能。
• 不能处理非球形分布：在某些数据分布下，欧氏距离可能不是衡量相似性的最佳方式。

六、与其他距离度量的比较

• 曼哈顿距离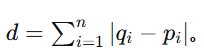：也称为“城市街区距离”，想象在棋盘状的城市街道上行走，不能走对角线。它对异常值不如欧氏距离敏感。
• 余弦相似度：衡量的是两个向量方向上的差异，而非距离或绝对数值。对于文本分析（如文档相似度）特别有用，因为它只关注角度，忽略向量的模长。

总结

欧氏距离是数据科学和机器学习中最基础、最重要的距离度量之一。它完美地捕捉了空间中的“直线距离”概念。尽管存在对量纲和异常值敏感等局限性，但在理解了其原理并经过适当的数据预处理（如标准化）后，它仍然是众多任务中强大而有效的工具。

好的，没问题！我们抛开复杂的数学术语，用一个非常生活化的方式来细化欧氏距离，让它变得通俗易懂。

一、一句话核心思想

欧氏距离，就是“两点之间的直线距离”。 就像你用一把尺子直接连接两个点量出来的长度。

二、细化示例：从生活到数据

示例1：找房子的抉择（二维空间）

想象你在找房子，最关心两个因素：通勤时间和月租金。你可以把每个房子看作一个点，画在一个二维图上：

• 横轴（X轴）：通勤时间（分钟）
• 纵轴（Y轴）：月租金（元）

现在有两个选择：

• 房子A： (通勤30分钟， 租金4000元)
• 房子B： (通勤60分钟， 租金3000元)
• 你的理想房子P： (通勤20分钟， 租金3500元) - 这是你的基准点。

问题： 哪个房子更接近你的理想？

欧氏距离来帮忙！ 我们计算每个房子与理想房子P的直线距离。

1. 计算房子A与P的距离：
   1. X轴差距：30 - 20 = 10分钟
   2. Y轴差距：4000 - 3500 = 500元
   3. 距离 = √(10² + 500²) = √(100 + 250,000) ≈ 500.1
2. 计算房子B与P的距离：
   1. X轴差距：60 - 20 = 40分钟
   2. Y轴差距：3000 - 3500 = -500元（取平方后负号消失）
   3. 距离 = √(40² + 500²) = √(1600 + 250,000) ≈ 501.6

结论： 房子A（500.1）比房子B（501.6）在“通勤-租金”这个二维空间里，更接近你的理想。尽管房子B租金便宜了500元，但它通勤时间太长，综合来看，反而不如房子A均衡。

这个例子的精髓： 欧氏距离帮我们综合考量多个因素，做出一个“整体最优”的判断，而不是只看单一维度。

示例2：精准推荐电影（三维空间）

假设一个电影推荐系统用三个指标来描述一部电影：

• X轴：喜剧成分
• Y轴：动作成分
• Z轴：浪漫成分

每部电影都是三维空间中的一个点。比如：

• 《王牌逗间谍》： (喜剧90， 动作70， 浪漫10)
• 《泰坦尼克号》： (喜剧10， 动作20， 浪漫95)
• 你刚点赞的《杀手保镖》： (喜剧80， 动作85， 浪漫30) - 这是你的喜好基准。

问题： 系统应该给你推荐哪一部？

欧氏距离再次出手！ 计算其他电影与你喜好电影的“口味距离”。

1. 《王牌逗间谍》到《杀手保镖》的距离：
   1. √[ (90-80)² + (70-85)² + (10-30)² ] = √[100 + 225 + 400] = √725 ≈ 26.9
2. 《泰坦尼克号》到《杀手保镖》的距离：
   1. √[ (10-80)² + (20-85)² + (95-30)² ] = √[4900 + 4225 + 4225] = √13350 ≈ 115.5

结论： 《王牌逗间谍》的口味距离（26.9）远小于《泰坦尼克号》（115.5），所以系统会优先将《王牌逗间谍》推荐给你。因为它和你的喜好“靠得更近”。

三、细化应用场景（它们到底怎么用？）

场景1：K-最近邻分类 - “物以类聚，人以群分”

• 干什么用？ 比如银行要判断“是否应该给一个人发放贷款”。
• 怎么用欧氏距离？银行有过去客户的资料，包括年龄、年收入、负债比（三个维度）。
  • 每个客户已经被标记为“好客户”或“坏客户”。
  • 现在来了一个新申请人，他的数据是（年龄35， 收入50万， 负债比40%）。
  • 系统会计算这个新申请人与历史上所有客户的欧氏距离。
  • 找出距离最近的K个（比如K=5）“老邻居”。
  • 决策： 看看这5个邻居里，大部分是“好客户”还是“坏客户”。如果5个里有4个是好客户，那就认为这个新申请人也是好客户，可以贷款。

场景2：K-均值聚类 - “自动分堆”

• 干什么用？ 比如电商公司想对客户进行分群，以便精准营销。
• 怎么用欧氏距离？收集所有客户的年消费额、购买频率、平均客单价（三个维度）。
  • 算法会随机设定几个“簇中心”（比如想分成3类，就设3个中心点）。
  • 第一步（分配）： 计算每个客户到3个簇中心的欧氏距离，将他归入距离最近的那个中心所在的簇。这样所有客户就被分成了3堆。
  • 第二步（更新）： 重新计算每个簇的“中心点”（通常是这个簇里所有点的平均值）。
  • 重复第一步和第二步，直到中心点不再剧烈变动。
  • 结果： 你得到了3个清晰的客户群体，比如“高价值常客”、“低频大额客户”、“低价值流失客户”，然后可以对不同群体采取不同的营销策略。

场景3：异常检测 - “找出害群之马”

• 干什么用？ 检测信用卡盗刷、工业零件瑕疵。
• 怎么用欧氏距离？收集正常信用卡交易的数据，如交易时间、金额、地点、商户类型等（N个维度）。这些正常的交易点在空间里会聚成一团。
  • 当有一笔新交易发生时，计算它到那个“正常点团”的中心（或最近邻点）的欧氏距离。
  • 如果这个距离远远大于大多数正常交易的距离，就被标记为“异常交易”，需要人工审核。因为它是一个“离群点”。

四、重要提醒（局限性）

“单位”不一样怎么办？

回头看找房子的例子，如果通勤时间用“小时”，租金用“万元”，公式变成：

距离 = √( (0.5-0.33)² + (0.4-0.35)² ) = √(0.0289 + 0.0025) = √0.0314 ≈ 0.177这个结果和之前用“分钟”和“元”算出的500完全不同，可能会导致决策错误！

解决方案： 在使用欧氏距离前，必须对数据进行标准化，把所有特征缩放到同一个尺度上，比如都变成0到1之间的数，这样才能公平地比较。