归并排序的实现

wyuchen123

已于 2024-06-07 20:37:49 修改

阅读量826

点赞数 20

分类专栏： # 基础算法文章标签： c++ 算法排序算法归并排序

于 2024-05-11 08:00:00 首次发布

本文链接：https://blog.youkuaiyun.com/wyuchen123/article/details/137407497

版权

基础算法专栏收录该内容

18 篇文章

订阅专栏

这是C++算法基础-基础算法专栏的第三篇文章，专栏详情请见此处。

引入

归并排序是一种常用的稳定排序算法，这种算法对于求逆序对问题大有用武之地。

下面我们就来讲归并排序的实现。

定义

归并排序（merge sort）一种是高效的基于比较的稳定排序算法。

过程

归并排序的工作原理是通过分治的原理来将一个数组排序。共分为三个过程：

将数列划分为两部分；
递归到两个子序列中分别进行排序；
合并两个子序列，将合并后的数组存入原数组中。

第一步，为保证排序的复杂度最优，我们取中点进行划分，即 $mid=\left \lfloor \frac{l+r}{2} \right \rfloor$ 。

第二步，就是调用两端递归函数。

第三步，维护两个指针 $i$ 和 $j$ ，从左往右枚举左右两个数组，找出最小的值并放入数组 $t$ 中，例如，对于左半数组与右半数组 $a$ 与 $b$ ，当前若 $a\left [ i \right ]<b\left [ j \right ]$ ，则将 $a\left [ i \right ]$ 放入 $t\left [ k \right ]$ 中，然后 $i++$ 、 $k++$ 。最后直到 $a$ 与 $b$ 有一个为空时，将另一个数组剩下的元素放入 $t$ 中。最后，当合并完成后，再将已排序后的临时数组存入原数组中。

归并排序是一种稳定的排序算法，为了这个性质，合并时，当 $a\left [ i \right ]=b\left [ j \right ]$ 时，优先考虑将 $a\left [ i \right ]$ 放入 $t\left [ k \right ]$ 中。所以你可以在代码中看到，将 $a\left [ i \right ]$ 放入 $t\left [ k \right ]$ 中的判定条件为 $a\left [ i \right ]\leq b\left [ j \right ]$ 。

~~说实话，排序算法的稳定性其实并没有什么卵用。~~

下面给出归并排序思想图：

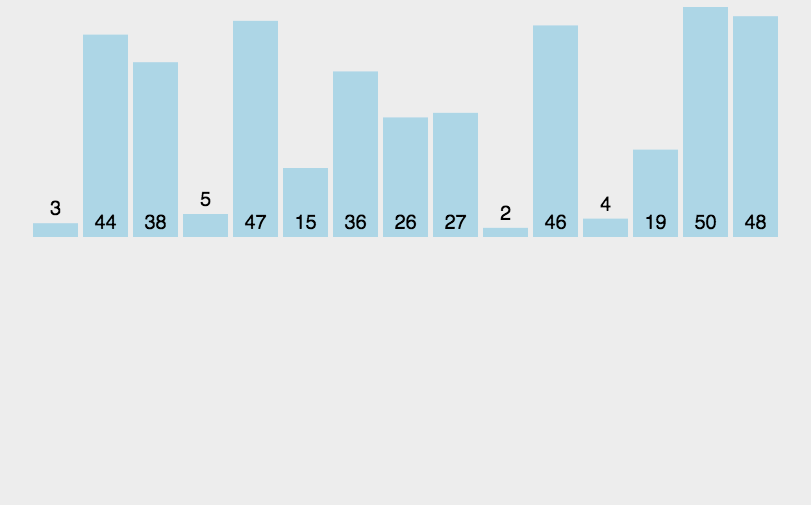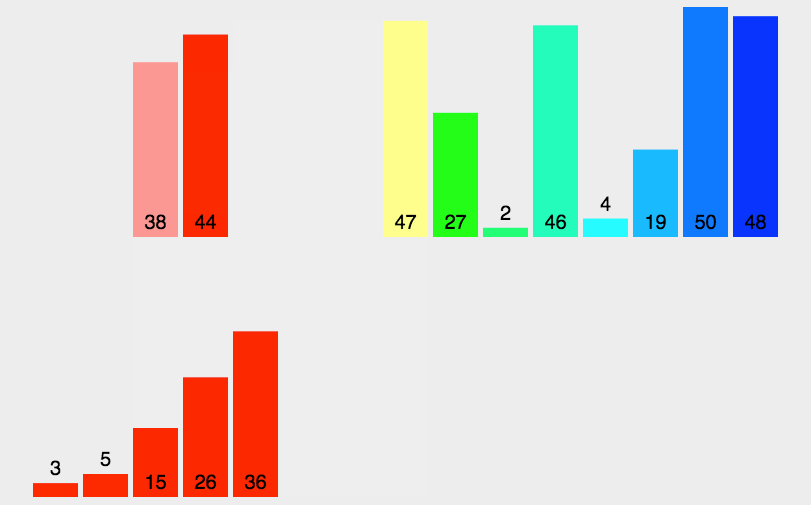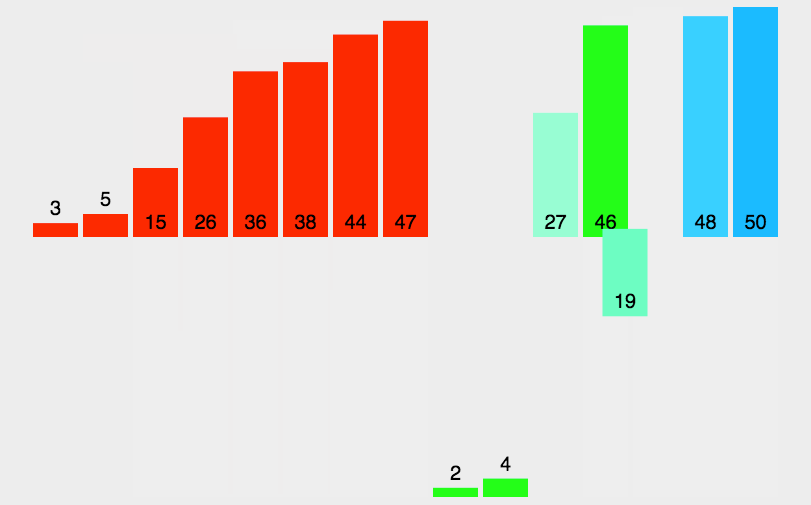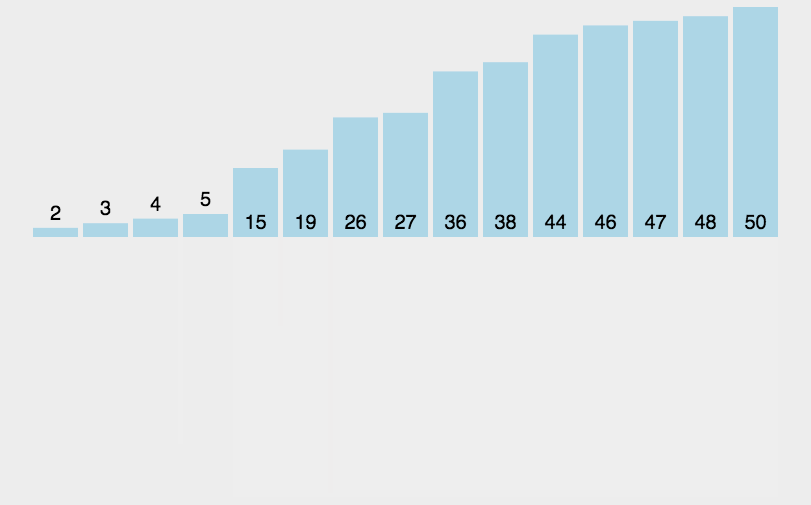
性质

稳定性

归并排序是一种稳定的排序算法。

时间复杂度

归并排序的平均、最好与最坏时间复杂度均为 $O\left ( nlog_{2}n \right )$ 。

Q：为什么归并排序的时间复杂度为 $O\left ( nlog_{2}n \right )$ 呢？

A：归并排序递归时每次都会从中间分开进行递归，整个递归的过程可以看作一棵二叉树。对于有 $n$ 个值的数组的归并排序，二叉树的叶子结点总共有 $n$ 个，则二叉树总共有 $log_{2}n$ 层；每层又都需要把数组合并在一起，合并的时间复杂度为 $O\left ( n \right )$ 。最后综合到一起，总的时间复杂度即为 $O\left ( nlog_{2}n \right )$ 。

空间复杂度

归并排序的空间复杂度为 $O\left ( n \right )$ 。

代码

下面给出归并排序的实现：

void merge_sort(int q[],int l,int r){
	if(l>=r)
		return;
	int mid=l+r>>1;
	merge_sort(q,l,mid);
	merge_sort(q,mid+1,r);
	int k=0,i=l,j=mid+1;
	while(i<=mid&&j<=r){
		if(q[i]<=q[j])
			tmp[k++]=q[i++];
		else
			tmp[k++]=q[j++];
	}
	while(i<=mid)
		tmp[k++]=q[i++];
	while(j<=r)
		tmp[k++]=q[j++];
	for(i=l,j=0;i<=r;i++,j++)
		q[i]=tmp[j];
}

上一篇-快速选择算法的实现 C++算法基础专栏文章下一篇-求逆序对问题的实现

每周六更新一篇文章，内容一般是自己总结的经验或是在其他网站上整理的优质内容

点个赞，关注一下呗~