写给新手的深度学习基础

原创已于 2025-03-02 17:23:57 修改 · 1.3k 阅读

35 ·

CC 4.0 BY-SA版权

文章标签：

#深度学习 #算法 #人工智能

于 2025-03-02 17:22:21 首次发布

前言

这篇文章是写给新手的，但是又是比较细致的。会从原理的角度出发，让读者逐渐明白深度学习是什么、神经网络是什么。不需要任何的门槛。希望这篇文章可以给你足够的启发和满足感。

不管如何，亲爱的陌生人，让我们静下心来读完这篇文章吧。种一棵树的最好时机就是现在！加油！💪！

1. 你从哪里来，又往哪里去？

1.1 深度学习与机器学习

深度学习（deep learning）是机器学习（machine learning）的一部分。机器学习是很好理解的，从名字上来看，就是让机器学习、做出判断。专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能。但是传统的机器学习算法依赖人去进行特征工程，用人去手动找出数据的特征，而深度学习则不需要。深度学习可以自己去发现、寻找数据的特征！这就是深度学习来自于机器学习，又区别于机器学习的地方。

1.2 深度学习的灵魂

那么，深度学习是如何做到“自己寻找特征”的呢？这就说到了深度学习的“灵魂”——神经网络🤯。神经网络本质上是一层又一层的矩阵运算（也可能是卷积等其他的，但是运算的过程其实都可以看成在做矩阵运算🔢），每一次的运算，在原有的基础之上，抽象出更加高维的特征。（没错，就这么抽象😅，笔者在最开始学习的时候也觉得抽像极了，但是往后就会发现越来越妙🤩）

1.3 深度学习的未来

正是因为深度学习通过神经网络技术实现了对特征的主动提取，省略了大量的人力，所以获得了更加广阔的发展空间。随着其逐渐的发展，才慢慢诞生出了现在的DeepSeek、ChatGPT （如果要写一本人类史，它们都可以用来当某一章的标题了）。

神经网络技术是收到了我们大脑的启发（也算的仿生学的高光时刻了）而诞生出的技术。我们的大脑其实就是可以自己进行特征工程的。我们小时候没有人告诉我们如何识别母语的发音，我们自己就学会了说话。没有人告诉我们如何判断一个树是树，父母只是告诉我们这样的物体叫树，我们就能认出所有的树。我们的大脑自己就可以提取事物的特征，并且将这些特征同“树”这个意象联系起来，而且学习的很快。这是 38 亿年进化的成果，固然是惊人的、优秀的。而目前我们正在尝试通过自己的造物，来模仿这一进化的成果，发展的最终结果也终将的颠覆的，并且我们人脑能做到的事，未来我们的深度学习也终将都能做到并且超越。只不过目前我的模仿还很拙略。虽然在单个领域，我们的深度学习技术表现已经远远超过了人类大脑，深度学习可以在很短的时间对大量的图片中的多个物体进行快速、准确的识别。但是，训练这一模型的消耗能量却远超过人类大脑。从性价比的角度去看，咱们还得继续努力😋。

2. 最基本的一层神经网络

2.1 最基本的一层

下面的内容需要读者具备矩阵运算的最基本的知识，知道两个矩阵相乘是如何运算的就好。还不熟悉的同志可以点一下这个超链接👉我是超链接。

之前提到过，神经网络的最基本的一层其实就是一个矩阵运算，可以如下表示：

$f(X,W) = W\cdot X+B$

其中， $f(X,W)$ 叫做得分函数、矩阵 $X$ 是这一层的输入，其可以是我们处理后的数据，也可以是上一层运算出的结果，但是在数学上需要是一个列向量。矩阵 $W$ 是这一层的所有参数，也可以看做一个矩阵，它觉得了这一层要输出的运算结果是一个多大的列向量。列向量 $B$ 就是一个偏置。

现在，我们讨论一个一层的神经网络，就是由上面👆这一层来组成的，它的输入是一张长宽都是 32 个像素的图片。但是我们目前这一层的输入只能是一个列向量，所以我们需要变形。目前这张图片可以看做是三个 32*32 的矩阵。为什么是三个？因为分别用三个矩阵来存储三原色的不同值，组合起来就是五彩斑斓的图片了。所以，要把这张图片输入到我们目前的这层神经网络中，我们需要将其转换成一个 3072*1 的矩阵（因为 32*32*3=3072）也就是我们的 X，而输出是一个 2*1 的矩阵。这是我们的要求。那么我们的 W 就应该是一个 2*3072的矩阵了。（先不管 B 的事，因为它确实存在感比较低）。

那么显而易见这时一个对图像进行二分类的神经网络。我们可以想象一下它的用途（比如说判断这张画是莫奈画的还是梵高画的，或者判断这张图片是不是被 PS 过的等等，但是要注意，因为咱们现在的这个神经网络太简单了，效果不会很理想）。不管用途如何，我们因该如何实现这一用途呢？

还记得 $f(X,W)$ 叫什么吗？——“得分函数”。它其实就是我们的输出，是一个 2*1 的向量。我们要让这个得分函数计算出来的结果，越来越符合我们期望的那样。就那判断图片是否经过 PS 为例，那么得分函数得出的列向量中的两个值分别就对应了经过 Ps 的概率和没有经过 PS 的概率，然后再让机器判断哪个大，就能得出最后的结果。

那么如何让得分函数得到我们想要的得分呢？如何让它计算出我们想要的概率值呢？关键其实就是在 $W$ 上。 $W$ 就是我们的权重，我们所谓的“训练”，其实就是训练出合适的权重来。那么如何训练呢？我们先随机生成一个 $W$ ，是的，就是这么随意。然后用这个 $W$ 来进行初步的运算，运算出来的结果和我们实际的结果对比。如果不同，那么改良 $W$ ，接下来再带着新的 $W$ 来进行计算，再和结果对比。这是最基本的思想。目前再训练 $W$ 时最广为人知的就是随机梯度下降（SGD）和动量法（Momentum）以及一些对学习率进行自动调整的算法。这不是我们的重点（但是也很有趣）。

简单来说，我们需要优化 $W$ ，来让我们的得分函数得出我们想要的得分。那么问题来了，优化算法咱们已经有了，但是我们在训练过程中，如何告诉机器得分函数错了？以及如何告诉机器得分函数错了多少？

2.2 损失函数——“该罚！”

简单来说，损失函数就是将目前预测值和真实值的差距抽象成一个具体的数值，告诉机器错没错，以及错了多少。错的越离谱，损失函数的值越大。

2.2.1 对于二分类问题

对于单个样本的公式先给出来，大家细品，不难：

$L = -[y\log(\hat{y})+(1 - y)\log(1 - \hat{y})]$

其中，L 就是损失函数， $y$ 是这一样本的实际值，不是 0 就是 1（这时针对二分类的任务而言的，咱们举的这个例子就是二分类的，后面会介绍多分类的）。而 $\hat{y}$ 是咱们预测的经过，在咱的任务里，假定 $y$ =1 代表进行了 PS，那么 $\hat{y}$ 就是咱预测出的进行了 PS 的概率。那么这么看，这个公式就不难理解了吧，而且真实值和预测值差的越多，L 的值就越大！很给力。当然，这只不过是最基本的一种损失函数，而且还是针对二分类问题的。

我们在训练时，往往会一轮一轮的训练，也就是说我们往往会先便利完所有的样本，然后再求出整体的损失函数，调整后再编辑一轮，直到达到最大轮数或者其他要求。所以，对于一轮的损失函数的公式就成了这样子：

$L=\frac{1}{n}\sum_{i = 1}^{n}-[y_i\log(\hat{y}_i)+(1 - y_i)\log(1 - \hat{y}_i)]$

挺好理解的，就是加上了一个求和。而 $n$ 呢，就代表了样本数量。

2.2.2 对于多分类问题

先上公式：

$L=\frac{1}{n}\sum_{i = 1}^{n}\sum_{j = 1}^{C}y_{ij}\log(\hat{y}_{ij})$

这是对于一轮的整体的损失函数（n 个样本的数据集的多分类交叉熵损失公式）。其中 $y_{ij}$ 是一个独热向量（one-hot）。啥叫独热向量

2.2.3 损失函数引起的过拟合问题

有时候，罚的太过了容易出问题。我们在训练模型的时候，总是分成了训练集和测试集。训练集顾名思义用于训练，而测试集用于测试训练的成效。当我们完全按照损失函数走，不完全符合就该罚的时候，我们的训练会使得模型过于贴合我们的训练集，而失去泛化能力。换句话说，我们用训练集训练我们的模型的目的是为了让模型可以处理相同的问题，当我们过渡训练，或者完全按照损失函数去做的话，就相当于让模型背答案了，这时就没什么实际意义了！

2.3 正则化——防止过拟合的措施之一

当我们的模型出现过拟合的情况时，在 $W$ 上的表现为：该矩阵中有一些值是十分突出的。

为什么呢？如果说我们的 $W$ 中某些值是十分突出的，说明模型对于样本的判断主要依靠这些值对应的特征，而较少的利用到了其他的特征。一方面，我们训练集覆盖的种类不一定是全面的，当我们过渡训练时，我们的模型就会只关注我们训练集所涵盖的哪些种类；另一方面，虽然我们输出的列向量的大小是固定的（也就是神经元的个数，这个到后面会细说），但是列项中中的每一个值所抽象出来的特征是不一样的。这些特征可以是有利于模型泛化的特征，也可以是不利于模型泛化的特征（比如说我们在判断是否被 PS 时，不利于泛化的特征就是这个图的色调。我们的训练集中，可能被 PS 过的图片的色调分布较为集中，但是实际情况不是这样，被 PS 过的图片可以是任意色调的，这时我们如果过渡训练的话，可以输出的特征之中，就有可能抽象出“色调”这一特征。是的，即使我们固定了抽象出的特征数量，或者说是输出神经元的数量，但是也没有规定每一个神经元到底抽象出的是哪个特征，而且很多时候即使我们知道了这个神经元是如何计算的、知道了参数，也不能去解释为什么会这样抽象。话说回来，我们抽象出的“色调”这一特征因为在我们训练集中可以十分方面的判断是否经过 PS，所以其就会在训练中被抽象出来。但是这一特征是不利于模型泛化的。）而这些不利于模型泛化的特征，往往会在训练的时候其所占权重会越来越大。为什么？因为这一特征十分适用于我们的训练集，而我们一直在训练集上训练！所以这样也会导致我们的 $W$ 中的某些值十分的突出。

很明显，过拟合不是我们想要的，背答案真的一点意思也没有。那么如何防止呢？其实很简单——就是尽量防止 $W$ 中的某些值过于突出。那么如何防止呢？正是因为完全依照损失函数进行训练，才导致的正则化，所以我们应该在损失函数上做文章。我们要让损失函数不能一方面会因为预测结果于真实值又出入而增大的同时，也应该再加上一项去制约它——当 $W$ 中某些值突出时，也让损失函数加大。所以，损失函数的完全体诞生了（添加 L2 正则化项后的多分类交叉熵损失函数公式）：

$L_{L2}=\frac{1}{n}\sum_{i = 1}^{n}\sum_{j = 1}^{C}y_{ij}\log(\hat{y}_{ij})+\frac{\lambda}{2}\sum_{i}\sum_{j}W_{k}^{2}$

公式很好理解，跟在原有损失函数后面的就是正则化项。当然还有 L1 正则化的正则化项：

$\lambda\sum_{I}\sum_{j}|W_{k}|$

现在用的最多的就是L2。一般在数学上用 $\lambda R(W)$ 来代表正则化项。 $\lambda$ 的大小用来调整正则化的力度。如下如所示：

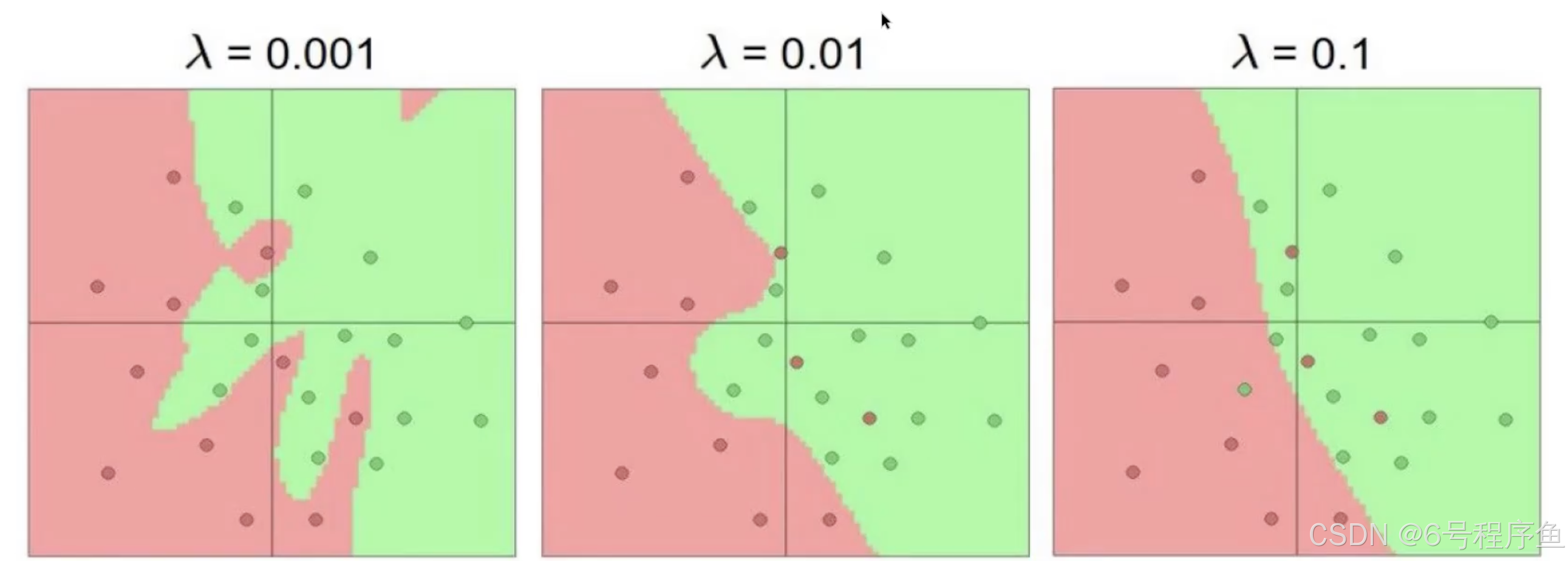
这张图的情景是这样的：我们在用一个神经网络（这个神经网络不只是单层的，其还加上了激活函数。什么是激活函数？后面会将。这里不会影响大家阅读）去做一个二分类的任务。咱们要通过坐标来预测这个点是红点还是绿点。当咱们的 $\lambda$ =0.001 时，咱们地模型划分地十分准确，在训练集上表现地很不错。但是大家想，这时候咱们模型的泛化能力真的好吗？

咱们训练模型，要处理的最终肯定是自然界的问题。自然界中任何事物的分布都是连续的（宏观上），大家看咱们的训练集中，是不是有一些红点不和谐的分布在了绿点之中？

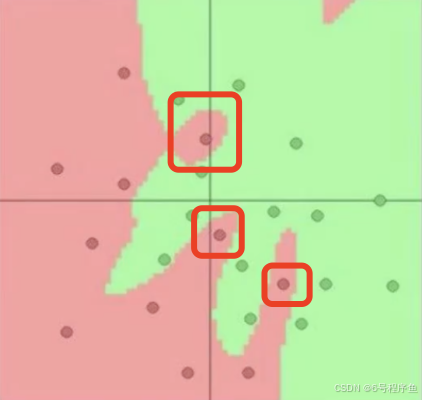
这些点很有可能是错误的数据点——或者说是异常值。我们在训练的过程中不能对这些异常值“百依百顺”。不然最终肯定会过拟合的。所以，我们增大 $\lambda$ 。大家可以看到，随着 $\lambda$ 的增加，咱们的模型划分的界限变得越来越平滑，这样子咱们模型的泛化能力就增加了。

但是也可以看出， $\lambda$ 不能过大。不然我们的模型就太“一意孤行”，开始请示预测值和实际值的差距了。

2.4 softmax分类器

我们现在只要用加上了正则化项的损失函数对模型的参数矩阵 $W$ 依照梯度下降法进行不断优化，就可以得出我们想要的结婚了......吗？其实还差一步😜。

还记得 $\hat{y}$ 是什么意思吗？是预测出的照片被 PS 的概率。是“概率”。而我们目前即使在优化 $W$ ，我们始终计算的不是概率，只不过是一次又一次的线性运算。所以最后咱们还要再加上softmax分类器：

$P(y=k \mid x) = \frac{e^{z_k}}{\sum_{j=1}^K e^{z_j}}$

它可以将每个类别对对应一个数值的情况转换成每个类别都对应一个概率的情况。而且所有类别的概率之和为 1。这样就可以计算出我们的 $\hat{y}$ 了。

2.5 总结

这就是最基本的一层神经网络的结构。其本质上是在进行一个矩阵运算，而我们通过对目前矩阵运算的经过和我们所期望的结果项目向比较，将不相符的程度通过加上正则化项的损失函数来表征预测值和实际情况的差异，随后根据这一差异，利用梯度下降法，来对 $W$ 进行不断的优化，最后达到我们想要的输出。 $W$ 的大小和我们的输入列向量、输出列项量的大小有关（也可以说这一层的输入列向量的大小与这一层的神经元个数有关）

但是，大家估计在阅读的时候也能感受到，一层网络是不是有点鸡肋？没错，这确实很鸡肋。其实大家可以仔细想一想，一层神经网络，在二分类问题中，其实就是一个多维的线性拟合，只不过维数比较多。所以，往往咱们实际应用中的神经网络都是多层的。正式多层神经网络才让我们的深度学习有了非线性。

3. 多层神经网络

3.1 激活函数

多层神经网络不是简单的多个单层神经网络的叠加。在每一层神经网络后面，或者说在层于层之间，还有一个激活函数（activation function）。这些激活函数是非线性的。如果没有这些激活函数，那么整个模型其实就是连续地几个矩阵运算，最终还是可以结合成一个总的矩阵运算，到最后还是线性的。

下面给大家介绍一些著名的激活函数。大家不用一个个都背，但是最好注意一下他们的特性。

3.1.1 Sigmoid

表达式为：

$\sigma(x) = \frac{1}{1 + e^{-x}}$

图像为：

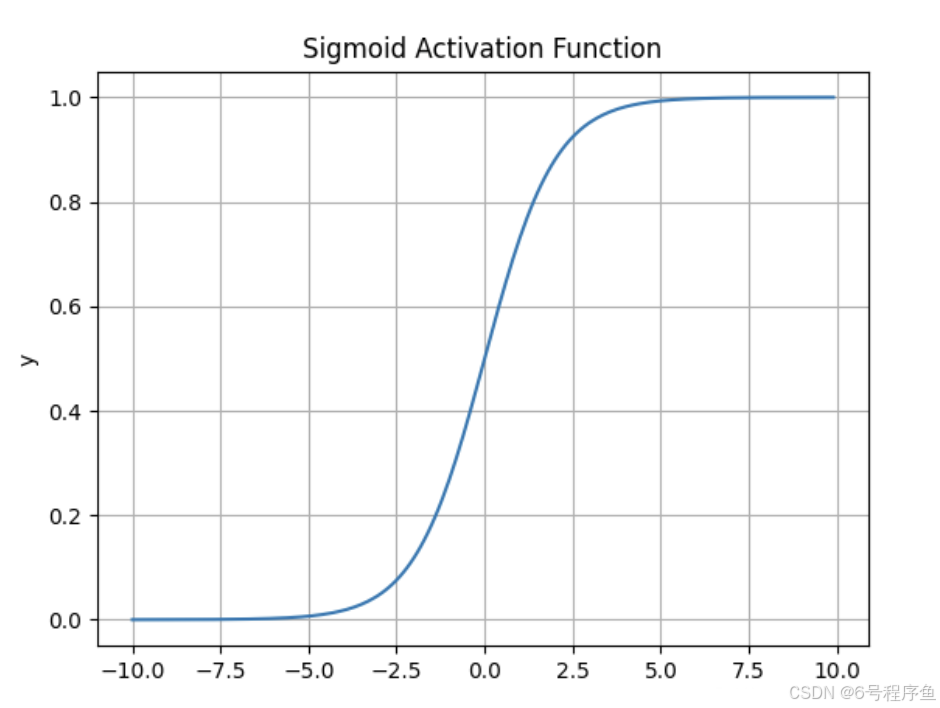
这个函数，现在不太常见了😅。因为它虽然是非线性的，但是会引起令人头疼的梯度消失的问题。具体什么是梯度消失，后面再给大家详细的介绍。

---------⌛️等待更新⌛️---------

下面再给大家讲解一下神经网络的前向传播于反向传播。这部分内容是为了让大家在读文献的时候更加得心应手，对于神经网络的实践影响不大。

3.2 前向传播

神经网络在训练过程中，有数据的前向传播和反向传播。

前向传播就是数据从输入到最后求出结果和损失函数之值的流程，也就是一个个的矩阵乘法再加上一个个的激活函数。这一过程在模型训练和模型应用的时候都会发生（当前，在模型应用时就不会涉及到求解损失函数了）。最终模型在求解时，前向传播用数学形式去表达，可以是（假设这是一个三层的神经网络）：

$S = af_3\{W_3*af_2[W_2*af_1(W_1*X+B_1)+B_2]+B_3\}$

其中 $S$ 就是最后的得分（还记得最开始的得分函数吗？）， $af_n()$ 是第 n 层的激活函数。

另外，在多层神经网络中，损失函数中往往有多个正则化项。

3.3 反向传播

向后传播发生在梯度求解的过程之中。这涉及到高等数学中的链式法则。链式法则通俗来讲就是在复合函数中，梯度是一步一步传播的。我们在进行模型的训练时，会通过梯度下降法来优化参数矩阵。虽然大家可能不了解梯度下降法的具体流程，但是大家肯定能看出来，我们躲不开一个“求梯度”的操作。而这个求梯度的操作就是进行了反向传播。

我们在求梯度的过程中，往往会从最终的经过出发，从后往前地去逐步计算梯度，所以这一过程被叫做反向传播。

具体的详细讲解，请大家移步到这篇文章去了解。超链接🔗（但是推荐大家先看完本文章，了解完了大体再去了解细节）

3.4 过拟合风险

多层神经网络即使我们进行了正则化处理，还是会有过拟合风险的。下面给大家看个例子：

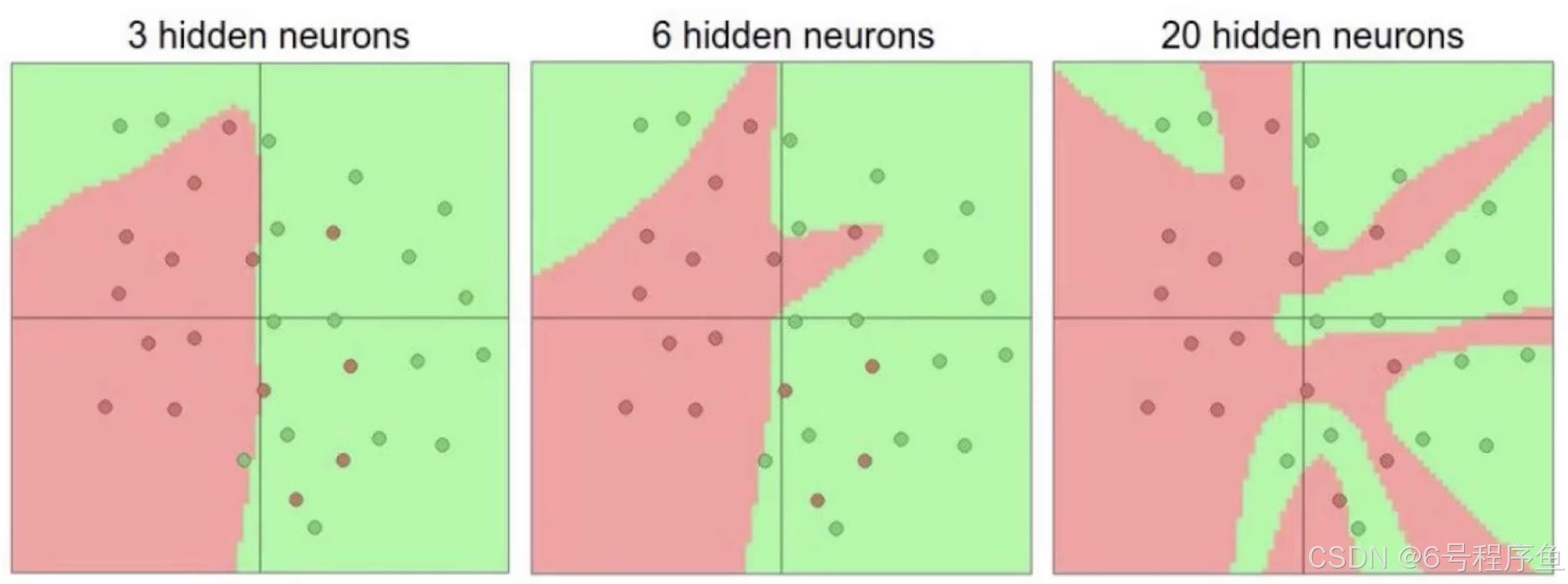
在上图中，大家可以看到，如果把整个平面看成一个蛋糕的话，随着中间层（或者叫隐藏层，也就是出去输入和输出层之外的左右层。但是激活函数不算一层哦😯）的增加，咱们分割蛋糕是所切的“刀数”也在增加。

这一方面代表着咱们模型得以适应更加复杂的情况，另一方面代表了咱们模型更加容易出现过拟合的问题。到底是因为咱们的模型太灵活了的话，很容易训练出一个完全贴合训练集的数据。这时候就又是在“背答案”了🤬。

3.5 Drop-out

过拟合当然是我们不想看到的。为了解决层数过多带来的过拟合问题，人们提出来 drop-out 的思想。这一思想其实很简单：

在每一轮的模型训练时，从目前的所有神经元中，随机选取一些来“杀死”（文献上习惯用“杀死”这个词，但是我们换成“沉默”更好理解。下面我还是用“杀死”，大家如果觉得不好理解的话，可以带换成沉默）。“杀死”也就是说在这里轮训练中，这些被杀死的神经元不参与参数的更新。但是要注意，这只是在“这一轮”当中，下一轮会重新进行随机的选择。所以如果我们在训练模型时采用 drop-out 策略，那么我们每一轮参与训练的神经元都是“部分的”。经过实践证明，这样可以很好的缓解层数过多带来的过拟合问题！😇