基于约束的因果发现方法

一、PC（Peter-Clark）算法

PC算法（Peter-Clark算法）是一种经典的贝叶斯网络结构学习方法，核心目标是从观测数据中推断变量间的因果关系或条件独立关系，构建有向无环图（DAG，即贝叶斯网络）。

PC算法过程：

1.先将所有变量进行连接，从而获得一个完全无向图。

2.通过条件独立性（d-separation）测试删除多余边获得骨架图。

3.随后识别骨架图中的对撞结构（v-结构），可以确定部分边的方向。

4.在确定所有对撞结构之后，通过DAG图的性质和Meek规则尝试确定剩余边的方向。

 一、获得完全无向图

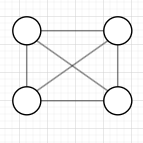
二、 获得骨架图

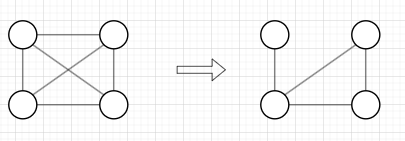
 条件独立性常用的方法为Finsher-z检验。由于PC算法假定所有的变量服从多元高斯分布，那么我们可以通过计算偏相关系数来判断变量之间是否条件独立。

偏相关系数定义：

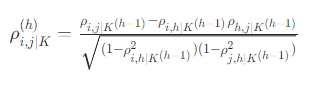
对于任意两个变量i和j，在排除h个其他变量（可能是变量总数等相关量） 影响后的阶偏相关系数。

该公式通过已有的低阶相关系数来计算当前阶的偏相关系数 ，体现了在控制特定数量变量后两变量的关联程度。

FisherZ变换

为了检验偏相关系数是否为0，需要将其通过Fisher Z变换转化为正态分布：

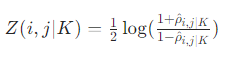
 原假设：ρ = 0，给定条件k下，变量i和j之间不存在条件相关性，即条件独立

备择假设：ρ ≠ 0

三、识别对撞结构

DAG图的构成主要分为三个结构：链式，叉式，对撞式

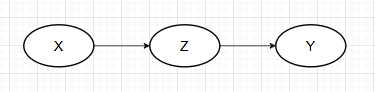
且

链式

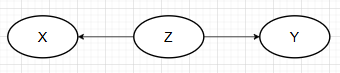
 且

叉式

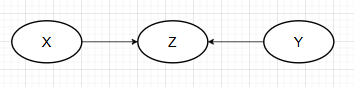
 且

对撞式

上述三种结构，只有对撞式中，固定变量Z时，变量X和变量Y由独立变为不独立。由此性质，我们可以找出骨架图中的对撞式结构。

四、确定剩余边的方向

 Meek规则：

1.避免产生新的碰撞：

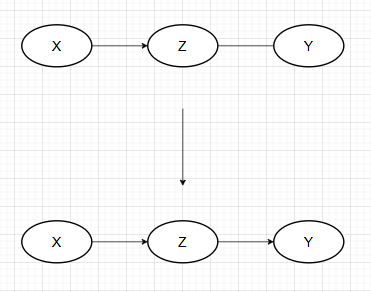
2. 避免成环：

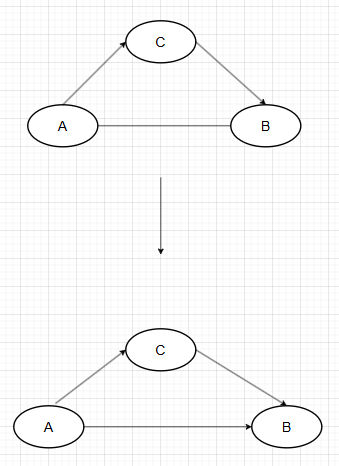
3. 避免生成新的碰撞结构（2）

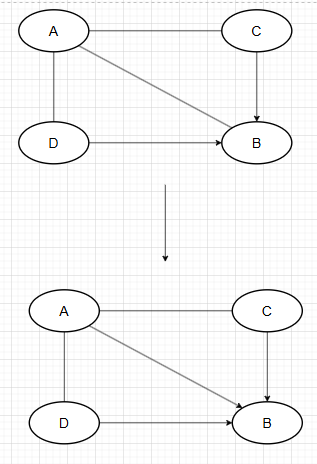
如果上述图，将AB边识别为A <- B时，由于D->B,C->B已知，为了避免成环，那么AD和AC边可以定下方向，即为A<-D, A<-C。

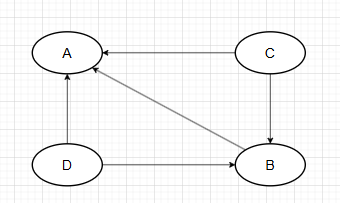
 该图出现了新的对撞结构D->A<-C

故AB边的方向为A->B

4. 避免生成新的碰撞结构（3）

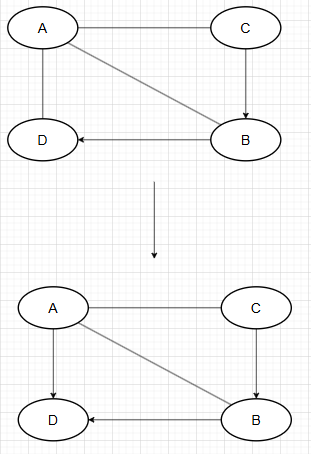
 如果上述图，将AD边识别为D -> A时，由于B->D已知，为了避免成环，那么AB边可以定下方向，即为A<-B

又由于B<-C ，为了避免成环，AC边可定下方向，即为A<-C

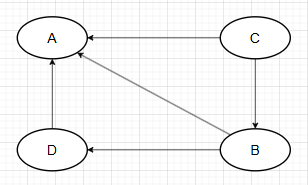
 该图出现了新的对撞结构D->A<-C

故AD边的方向为A->D

到此，可以生成一个部分有向无环图，PC算法结束。

二、FCI算法

FCI算法是PC算法的延申，PC算法假设所有的因素都被观察到，没有混杂因素影响，FCI则考虑了存在混杂因素。并且FCI的结果不为DAG图，为PAG图（部分祖先图）。

FCI会识别出双箭头的情况，当出现双箭头时，表示变量之间出现混杂因子。

FCI算法过程：

1.先将所有变量进行连接，从而获得一个完全无向图。

2.通过条件独立性（d-separation）测试删除多余边获得骨架图。

3.随后识别骨架图中的对撞结构（v-结构），可以确定部分边的方向。

4.在确定所有对撞结构之后，通过Meek规则尝试确定剩余边的方向。

注意：FCI在构建边时会分别判断一条边的两侧是否该出现箭头，并且边的两侧互不影响。

可能出现边的情况：

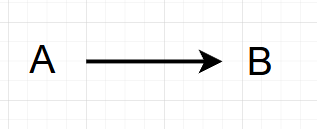
 A是B的因。

可能是直接原因也可能是包含其他可观测变量的间接原因。同时AB之间也可能存在不可观测的混杂因子。

消除可能：

        B不是A的因

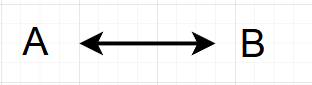
 存在不可观测变量（L）是A和B的共因。

从L到A或从L到B的因果路径上可能存在可观测变量。

消除可能：

        A不是B的因，B也不是A的因

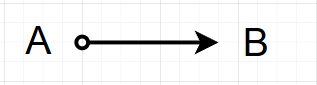
 A是B的因，或存在不可观测变量是A和B的共因，或二者皆有

消除可能：

        B不是A的因        

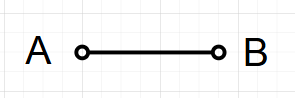
 这种类型的边表示下面情况中的一种：

(a) A是B的因
(b) B是A的因
(c) 存在不可观测变量是A和B的共因
(d) （a）和（c）同时发生
(e) （b）和（c）同时发生

后续过程与PC算法过程一致

但是对边方向的生成有所区别

例如：{X,Y,Z}，且存在未观测变量U影响X和Y：

假设真实的因果结构为：

{% asset_img Example.png Example%}

其中，L是一个潜在变量（不可观测）

PC算法：

由于 L 不可见，PC 算法无法解释 X 与 Y之间的相关性，只能认为它们之间可能存在直接关系。可能得到如下图：

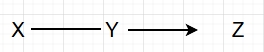
误导为 X 与 Y 有直接因果关系。

FCI算法：

FCI 可以检测到 X与 Y的相关性无法通过观测变量解释，因此使用 X\leftrightarrow Y表示它们之间可能存在潜在公共原因：

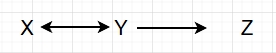
三、参考文献

PC算法详解 - 群青Bleu - 博客园 (cnblogs.com)

PAG简介 - 《Causality: Models, Reasoning, and Inference 中文翻译及读书笔记 - 因果关系:模型、推理和推理》 - 极客文档 (geekdaxue.co)

FCI — causal-learn 0.1.3.6 documentation

因果表征学习：问题，方法和应用 - 集智百科 - 复杂系统|人工智能|复杂科学|复杂网络|自组织 (swarma.org)