基于评分的因果发现算法

原创已于 2025-05-26 17:38:09 修改 · 631 阅读

15 ·

CC 4.0 BY-SA版权

文章标签：

#算法

于 2025-05-26 17:32:34 首次发布

一、背景

在基于分数的因果算法出现之前，通常都是使用基于约束的因果算法或者基于评分的方法进行因果发现任务。但是，在使用传统的基于评分方法时，需要对所有可能出现的因果结构进行评分，（如BIC）等，这意味着我们需要遍历所有可能的因果图（DAG），但是DAG的数量会随节点数呈指数增长，直接搜索会变为NP-hard问题，而NP-hard问题是难以解决的。
那么，我们怎么将NP-hard问题转化成其他问题呢？

如今有两种方式解决：

一：贪婪搜索（GES）

二：状态空间法

二、贪婪搜索（GES）

简单的来说，就是GES就是一个从数据中使用贪婪搜索学习贝叶斯网络的方法。

那为什么要弄出GES来呢，显而易见的好处就是，它不同于之前基于约束的PC算法等这一类要做条件独立性检验，这个基于评分的GES算法不需要做独立性检验，避开了独立性检验的缺陷，即无法识别马尔科夫等价类。

如何使用贪婪搜索？

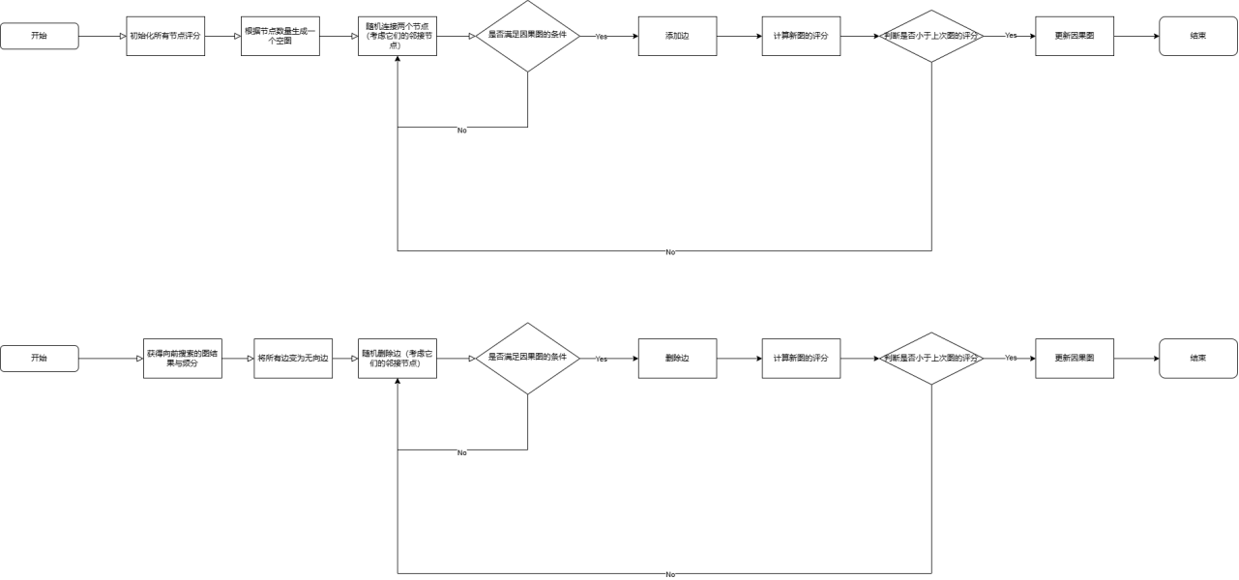
使用贪婪搜索寻找因果图过程：

1.初始化所有节点的评分

$BIC = n\ln(var(x))$

2.向前的贪婪搜索

首先输入一个空图，随后遍历所有的节点对（i，j）
随机链接节点对（i，j），同时检查不能有环，不能破坏现有v字结构，并且满足团条件（clique condition）

注：意思就是团(clique)就是一个无向图的完全子图，既然是完全图，当然每对顶点之间都必须要有边相连。

3.比较更新之后的图的评分和初始评分，当BIC变小时，更新图。

3.随后使用Meek规则，将部分无向边变为有向边

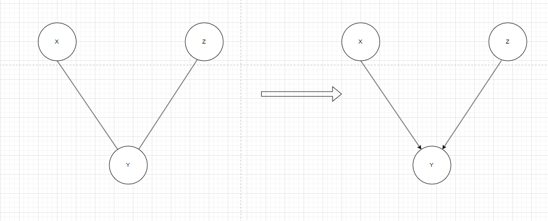
优先识别因果图中隐含的V-结构。

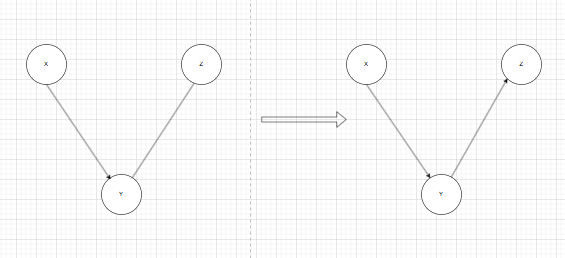
避免因保留 Y - Z 无向边而引入环（如 X →Y → Z → X）

4.向后的贪婪搜索

将所有有向边变为无向边
删除随机边，看是否满足DAG的条件，如果满足，便删除边，不满足便挑选其他的边进行删除
计算新图的评分，判断是否小于上次图的评分，如果小于，便更新因果图。

5.用Meek规则，将部分无向边变为有向边

三、状态空间法

我们可以引入状态空间法，将NP-hard问题转化为其他的问题。

在构建因果图的过程中，我们将空图视为初始状态，随后每加入一个或多个因素，视为新的状态。

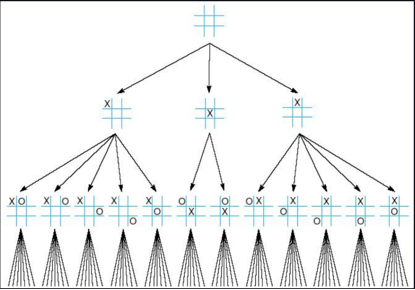
如果我们将空图视为起点，最优因果图结构视为终点，中间每一个结构使用评分方法得到评分（BIC）

那么，这个NP-hard问题便转化为了寻找最佳路径的问题。

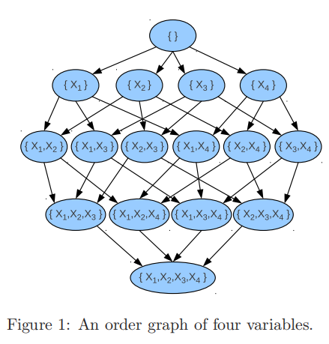
上图每一个节点都代表了节点中所含变量的所有因果结构。

例如：下面这个例子就表示为上图的一种方案。

那么，为了找到最佳路径，我们引入一个新概念：父集（Parent set）或父图（Parent Graph）

父图指的是某个节点（变量）在因果图中的直接原因集合，即该节点的所有父节点组成的子图结构。例如，在DAG中，若变量 X 的父节点为 {A,B}，则父图对应A→X 和 B→X 的结构。
基于评分的算法通过为每个节点选择最优的父节点集合，逐步构建全局因果图。

这里我们便可以定义BIC评分的函数为：

$BIC = n*ln(\frac{RSS}{n}) + k*ln(n)$

其中，k = 父集中节点个数，RSS = residual

当父集为空时，k=0

即选中的节点 $i$ 没有父节点，residual的计算公式为：

$residual = \sum_{j=1}^{n}X_{j,i}^{2}$

residual计算为当前结构评分的平方和。

当父集不为空时，k>0

当节点 $i$ 有父节点时，通过最小二乘法来拟合线性回归模型，设父集对应的矩阵为 $A = X[:,structure]$ ,目标节点为 $b = X[:,i]$ ,系数向量为 $\beta$ ，残差residual是拟合误差的平方和，即：

$residual = \left \| b-A\widetilde{\beta } \right \|$

现在，我们就得到了所有路径的分数。

这里有两种搜索最佳路径的方法：

1.A*搜索

2.Bellman-Ford算法

例如：

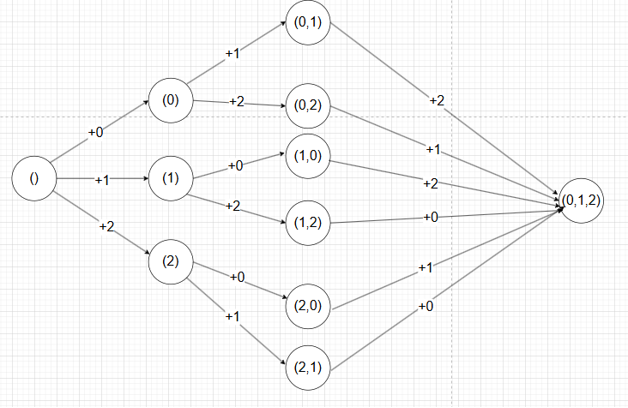
这个例子中，我们得到了所有的父集评分，对应的寻找最佳路径图像。

使用A*搜索时，

我们需要当前节点与起始点的距离，以及当前节点与目标节点的距离

$f = h + g$

其中f为总距离，g为当前节点距离起始点的距离，h为当前节点距离目标点的距离

假设，我们当前状态为（1，2）节点

那么，当前状态评分g即为{() ->(1)},{(1)->(1,2)},h即为{(1,2)->(1,2,0)}

g = 350.8256453955563+278.83836226229937 = 629.66400765785567

h = -6692.330897503053

f = -6,062.66688984519733

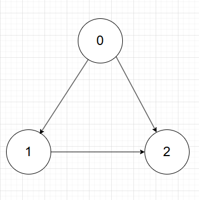
那么上述结构的评分便为 -6,062.66688984519733

使用Bellman-Ford算法时（什么是Bellman-Ford算法？）

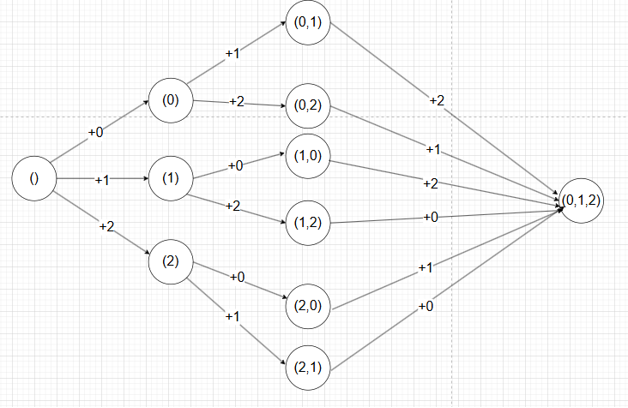
按照随机顺序不断更新从起始点空集，一直到终点最优结构的距离。

参考：

1. Score-based causal discovery methods — causal-learn 0.1.3.6 documentation

2.Huang, B., Zhang, K., Lin, Y., Schölkopf, B., & Glymour, C. (2018, July). Generalized score functions for causal discovery. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (pp. 1551-1560).

3.Chickering, D. M. (2002). Optimal structure identification with greedy search. Journal of machine learning research, 3(Nov), 507-554.

4.Bellman-Ford最短路径算法_哔哩哔哩_bilibili