LiNGAM因果发现算法

原创已于 2025-07-25 16:32:28 修改 · 2.1k 阅读

43 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #人工智能 #机器学习

于 2025-05-27 15:30:17 首次发布

LiNGAM全称Linear Non-Gaussian Acyclic Model ，即线性非高斯无环模型

以下所有的算法均满足LiNGAM的条件：

1.系统中所有因素满足线性关系

2.所有因素的噪声满足非高斯独立性

3.不存在未被观测到的混淆变量

基于 ICA 算法的因果模型识别（ICA-LiNGAM）

由于LiNGAM假设，我们能够得出结论：结果因素的分布就是由所有的被观测的因素线性相加而成。那么，我们就需要找到一个方法，将所有被观测的因素从结果因素的分布当中分离出来。

在信号处理的领域中，有一种方法叫做独立成分分析（ICA，independent component analysis），原本主要用于从多个混杂信号中分离出源信号，而今主要用于数据分析领域。

ICA的主要是基于非高斯假设，分离出方差相同、服从非高斯分布的多个源信号。

注：之所以设定方差相同，是为了将源信号变化幅度与混合信号矩阵进行区分。

假设某个源信号 $s_i$ 的幅度被缩放为 $\alpha s_i(\alpha \neq 0)$ ,同时混合矩阵的对应列 $a _i$ 被缩放为 $a _i/\alpha$ ,则乘积AS保持不变。这意味着：

源信号的幅度（方差）与混合矩阵的列向量幅度的乘积无法唯一确定。
若不施加约束，ICA的解将存在无限多组合（仅方向确定，幅度不确定）

有了以上假设，我们就可以将因素之间的关系转化为下面的公式：

$x = Bx + e$

其中， $x$ 表示为所有因素的矩阵， $B$ 为表示因果权重的矩阵（为了后续计算，通常我们将其变为对角线为零的下三角矩阵）， $e$ 为噪声项

$B$ 和 $e$ 是我们需要求得的。但是直接求比较困难，需要进行一系列变化。

经过行列式变换，我们可得：

$x = Ae$

其中， $A = {(I-B)}^{-1}$ （由于 $B$ 为下三角矩阵，可求逆矩阵， $A$ 为对角线不为零的下三角矩阵）。

由于我们假设噪声为高斯分布且相互独立，我们可以利用ICA的思想求解 $A$ ：

$X=AS$

$S=A^{-1}X$

经过类比，可得 $W = A^{-1}$ ,那么 $W = I-B$

这样通过计算，我们可以间接得到权重矩阵 $B$

FastICA

对于 $W$ 的计算，可以使用FastICA的方法进行计算

FastICA的核心是通过最大化非高斯性（如负熵）来估计评分。其理论基础是：

中心极限定理：多个独立随机变量的混合信号趋向高斯分布。因此，分离后的信号越非高斯，越接近独立源。
固定点算法：通过迭代优化快速逼近独立成分的解，避免传统梯度下降法的低效问题。

算法步骤：

（1）数据预处理

中心化（Centering）：将观测数据 X去均值，使其均值为零。

$X_{centered} = X - \mu$ , $\mu = \frac{1}{n}\sum_{i=1}^{n}x_i$

白化（Whitening）：对中心化后的数据进行线性变换，使其协方差矩阵为单位矩阵（消除相关性并归一化方差）。

通过线性变换 $Z = XP$ ，使得变换后的数据 $Z$ 满足：

$\frac{1}{n}Z^{T}Z = I$

即数据的协方差矩阵为单位矩阵（各维度不相关且方差为1）.

（2）选择非线性函数

FastICA 使用非线性函数（如 g(u)g(u)）近似非高斯性的度量。常用函数包括：

tanh（双曲正切）： $g(u) = tanh(au)$ （适用于亚高斯信号）。
Cubic（立方函数）： $g(u) = u^3$ （适用于超高斯信号）。
Gaussian（高斯函数导数）： $g(u) = uexp(-u^2/2)$ （通用性强）。

（3）对W进行迭代

1.初始化：随机选择初始权重矩阵W

2.迭代更新：

$W^+ = E\left \{ Xg(W^TX) \right \} - E\left \{ g'(W^TX) \right \}W$

其中g' 是 g 的导数，E表示期望

3.归一化： $W = W^+/\left \| W^+ \right \|$

4.收敛判断：重复迭代更新，直到 $W$ 位于阈值之内

（4）多成分提取（对称正交化）

为避免多个成分收敛到同一方向，每次提取新成分后需对矩阵 $W$ 进行正交化：

Gram-Schmidt 正交化：逐个去除已提取成分的投影。
对称正交化（更稳定）：同时对所有向量进行正交化（例如 $W = (WW^T)^{-1/2}W$ ）。

(5) 最大化负熵

$J = \sum_{i=1}^{p}k_i(E(f_i(W^TX))-E(f_i(v)))$

其中 $f_i$ 为非线性函数，v是高斯变量

由此，我们可以获得W，从而获得权重矩阵 $B$ 。

通过权重矩阵 $B$ ，可得因果结构以及关联系数。

ICA-LiNGAM的问题：

1.由于ICA-LiNGAM使用的是梯度算法，又用到了中心极限定理等，导致最终找到的解可能是局部最优而不是全局最优.

2.因果的方向由权重矩阵 $B$ 行变量顺序的决定，但是变量的缩放不同会影响行变量顺序，导致因果关系不稳定。

为了解决这个问题，Direct LiNGAM被提出。

Direct LiNGAM

Direct LiNGAM（Linear Non-Gaussian Acyclic Model）是一种直接从观测数据中推断因果结构的算法，由Shimizu等人提出。它基于线性、非高斯和无环的假设，通过逐步确定变量的因果顺序，最终构建有向无环图（DAG）

算法步骤：

(1) 数据预处理

中心化：对每个变量去均值，确保误差项均值为零。
标准化（可选）：消除量纲影响，便于系数比较。

(2) 确定因果顺序

通过迭代选择外生变量（无父节点的变量），逐步构建因果顺序：

1.寻找外生变量：

对每个变量 $X_i$ ，计算其与其他变量的回归残差：

$r_i^{(j)}=X_i - \beta _{ij}X_j(j\neq i)$

检验残差 $r_i^{(j)}$ 与 $X_j$ 的独立性，若存在某个 $X_j$ 使得 $r_i^{(j)}$ 与 $X_j$ 独立，则 $X_j$ 是 $X_i$ 的外生变量（即无父结点，只有子节点的变量）

2.递归剔除：

将已确定的外生变量从数据中移除，在剩余变量中重复上述步骤，直至确定所有变量的因果顺序。（剔除外生变量后，LiNGAM的假设对于残差矩阵依然成立。）

例如：获得的Causal Order为[x1,x2,x3]，那么我们就可以认为存在以下路径：x1 -> x2, x1 -> x3, x2 -> x3

（3）估计因果效应

基于确定的因果顺序，通过最小二乘法或最大似然估计线性系数：

$X_i = \sum_{k\in Pa(i))}^{}\beta_{ik}X_k + \epsilon_i$

其中 $\epsilon_i$ 为非高斯噪声， $Pa(i)$ 表示 $X_i$ 的父节点集合。

(4) 验证与模型选择

残差非高斯性检验：验证估计的噪声项是否满足非高斯假设（如峰度检验）。
拟合优度评估：通过似然比检验或信息准则（BIC、AIC）选择最优模型。

示例说明：

假设变量集为{X,Y,Z}:

1.发现X是外生变量(残差 $Y-\beta _{yx}X$ 与 $X$ 独立，且 $Z-\beta _{zx}X$ 与 $X$ 独立)

2.在剩下的变量 $Y,Z$ 中，发现 $Y$ 是外生变量(残差 $Z-\beta _{zy}Y$ 与Y独立)

3.可得顺序为: $X\rightarrow Y\rightarrow Z$

4.拟合 $Y = \beta_{yx}X + \epsilon_Y$ 和 $Z = \beta_{zy}Y + \epsilon_Z$

VAR-LiNGAM

VAR-LiNGAM（Vector Autoregressive Linear Non-Gaussian Acyclic Model）是一种将时间序列分析与因果发现结合的算法，由Shimizu等人（2005年提出LiNGAM，后扩展至时间序列）开发。其核心目标是从多元时间序列数据中推断变量间的时滞因果与瞬时因果关系。

算法步骤：

(1) 数学建模：

在基于LiNGAM的数学模型的基础上（瞬时因果），添加上时滞因果：

$y_t = \sum_{k=1}^{p}B_ky_{t-k} + B_0y_t + e_t$

时滞因果项： $\sum_{k=1}^{p}B_ky_{t-k}$

行列式变化：

$y_t = \sum_{k=0}^{p}B_ky_{t-k} + e_t$

$(I-B_0)[y_t - \sum_{k=1}^{p}(I-B_0)^{-1}B_ky_{t-k}] = e_t$

最终为

$y_t-\sum_{k=1}^{p}M_ky_{t-k} = B_0[y_t - \sum_{k=1}^{p}M_ky_{t-k}] + e_t$

其中 $W = I-B_0$ ， $M_k = (I-B_0)^{-1}B_k$ , $n_t = (I-B_0)^{-1}e_t$

于是，我们只需要得到 $B_0$ 和每个k的 $M_k$ ，我们便可以推测出其他的 $B_k$

与此同时，我们可以将 $y_t-\sum_{k=1}^{p}M_ky_{t-k} = n_t$ 视为VAR模型的残差

(2)计算残差以及自回归矩阵 $M_k$

1.利用最小二乘法估计自回归模型

$y_k = \sum_{k=1}^{p}M_ky_{t-k} + n_t$

可得VAR模型的自回归矩阵 $\widehat{M}_k$

2.估计VAR模型的残差 $n_t$

$\widehat{n}_t = y_t - \sum_{k = 1}^{p}\widehat{M}_ky_{t-k}$

可将残差 $n_t$ 作为LiNGAM的因果变量

3.估计瞬时因果矩阵 $B_0$

由于 $n_t = B_0n_t + e_t$ ,

可以使用ICA-LiNGAM或Direct-LiNGAM的方法估计 $B_0$

4.估计时滞矩阵 $B_k$

$\widehat{B}_k = (I-\widehat{B}_0)\widehat{M}_k (k>0)$

RCD-LiNGAM

RCD-LiNGAM（Repetitive Causal Discovery LiNGAM）假设了基本LiNGAM模型的扩展到隐藏的共同原因案例，即潜在变量LiNGAM模型。主要解决含有隐混杂因子的问题。

同样，RCD-LiNGAM的方法需要变量满足：

1.线性

2.非高斯连续误差变量

3.无环性

然而，RCD允许隐藏的共同原因的存在。它输出一个因果图，其中双向弧线表示具有相同隐藏共同原因的一对变量，有向箭头表示不受相同隐藏共同原因影响的一对变量的因果方向

具体实施过程：

1.子集随机采样

随机抽取子集，子集的大小常为3~5个，这个子集集合我们称之为 $S$

2.局部外生变量检测

在子集 $S$ 上执行：

对每个子集中的变量与剩下的变量进行线性模型拟合：

$X_j = \sum_{k\neq j}b_{jk}X_k+e_j$

其中 $X_j\in S$ ,我们检验残差 $e_j$ 是否满足：

非高斯性
是否与 $X_k$ 独立(HSIC或者Distance Covariance检验)

若 $e_j$ 与 $X_k$ 相互独立，则 $X_j$ 为外生变量

若 $e_j$ 与 $X_k$ 不相互独立，则 $X_j$ 不为外生变量，意味着有隐变量 $L$ 同时影响着 $X_j$ 和 $X_k$

若子集 $S$ 中没有外生变量，推断该子集被隐变量污染，重新进行子集抽样

若发现有外生变量，例如： $e_j$ 与 $X_k$ 相互独立，则 $X_j$ 为外生变量，我们可以认为在该子集中是 $X_k$ 的原因，我们可记为 $X_j\rightarrow X_k$

3.动态移除局部外生变量

当子集 S中发现外生变量 $X_j$ ，记录其指向的子节点边 $X_j\rightarrow X_k$ （ $X_k\in S$ ）

随后将 $X_j$ 从全局集 $V$ 中移除（因其因果顺序已确定）

在缩小后的 $V'=V \setminus X_j$ 上继续重复采样

4.终止条件

成功终止：所有变量被移除（因果顺序完整）

未成功终止：剩下的子集无法再找出局部外生变量，我们无法得到变量之间的因果关系，使用双箭头将所有的变量链接

CAM-UV

CAM-UV(Causal Additive Models with Unobserved Variables)它是对基本的因果加性模型进行扩展，以纳入未观测变量。该方法做出以下假设：

1.直接原因对变量形式的广义加性模型（GAMs）的影响
2.这些因果结构构成了有向无环图（DAG）

CAM

CAM是一种非线性因果发现方法，其核心思想是：

模型：

$X_i = \sum_{j\in PA(i)}f_{ij}(X_j) + \varepsilon_i$

其中：

$PA(i)$ 是变量X_i的直接因变量（父节点）；
$f_{ij}$ 是某种非线性函数（如spline）
$\varepsilon_i$ 是误差项，通常假设相互独立

CAM-UV 允许存在未观测变量。它输出一个因果图，其中无向边表示具有未观测因果路径（UCP）或未观测后门路径（UBP）的变量对，有向边表示不具有 UCP 或 UBP 的变量对的因果方向。

UCP 和 UBP 的定义：如图所示，从 xj 到 xi 的因果路径称为 UCP，如果该路径以连接 xi 及其未观测直接原因的有向边结束。如果一条后门路径从连接 xi 及其未观测直接原因的边开始，并以连接 xj 及其未观测直接原因的边结束，则该路径称为 UBP。

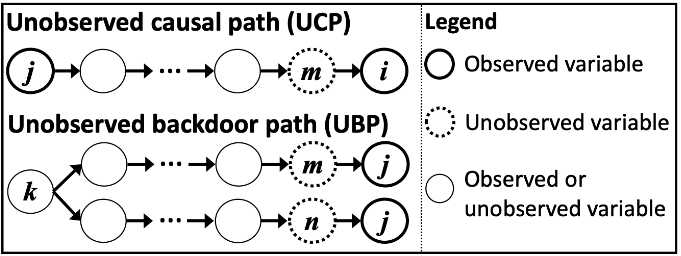
算法步骤：

1.拟合CAM模型

$X_i = \sum_{j\in PA(i)}f_{ij}(X_j) + \varepsilon_i$

其中：

$PA(i)$ 是变量X_i的直接因变量（父节点）；
$f_{ij}$ 是某种非线性函数（如spline）
$\varepsilon_i$ 是误差项，通常假设相互独立

2.检验残差独立性

拟合每个 $X_i$ 的父节点后，获得残差 $\varepsilon _i$

检查所有残差之间的独立性；

若有些残差之间不相互独立，说明存在潜变量影响

（因为拟合的都是可观测变量之间的关系，如果有未观测变量，其影响将会存在所有被影响变量的残差项当中，显示的就是不相互独立）

3.更改图

若两残差高度相关，删除该边（视为 latent confounding）；
若识别到不一致的方向，调整方向或设置为“undirected”

参考资料：

非时序线性非高斯模型 —— LiNGAM - 知乎 (zhihu.com)

独立成分分析 | Independent Component Analysis_哔哩哔哩_bilibili

Direct-LiNGAM算法理解_directlingam-优快云博客

【因果系列】基于 VAR 的线性非高斯模型 - 知乎 (zhihu.com)

RCD — LiNGAM 1.10.0 documentation

CAM-UV — LiNGAM 1.10.0 documentatis