【刷题那些事】Leetcode精选二叉树例题+解析

最新推荐文章于 2025-07-05 16:03:52 发布

温文艾尔

最新推荐文章于 2025-07-05 16:03:52 发布

阅读量1k

点赞数 28

CC 4.0 BY-SA版权

分类专栏：数据结构与算法文章标签： leetcode 算法 java 数据结构后端

本文链接：https://blog.youkuaiyun.com/wenwenaier/article/details/121930679

数据结构与算法专栏收录该内容

29 篇文章

订阅专栏

本文详细解析了LeetCode上的多个二叉树问题，包括计算二叉树所有左叶子之和、找树左下角的值、路径总和I和II、从中序与后序遍历序列构造二叉树、从前序与中序遍历序列构造二叉树以及构造最大二叉树。通过递归和层次遍历等方法，深入理解二叉树操作技巧。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

🙏亲爱的朋友，如果对你有帮助，给博主一个免费的点赞以示鼓励把QAQ☺

这里是温文艾尔の刷题学习之路
🙏作者水平欠佳，如果发现任何错误，欢迎批评指正
👋博客主页温文艾尔の学习小屋
👋更多文章请关注温文艾尔主页
👋超详细Leetcode刷题解析！
👋更多文章：
👋Leetcode刷题日记精选例题（附代码+链接）1
👋LeetCode刷题日记精选例题（附代码+链接）2
👋LeetCode刷题日记精选例题（附代码+链接）3
👋LeetCode刷题日记精选例题（附代码+链接）4
👋LeetCode刷题日记精选例题-双指针经典问题总结
👋LeetCode刷题日记精选例题（解析+代码+链接）5
👋11道精选经典LeetCode例题让你彻底搞懂二叉树的广度优先遍历
👋LeetCode刷题日记精选例题（附代码+链接）6

在这里插入图片描述

文章目录

👋计算二叉树所有左叶子之和
👋找树左下角的值
👋路径总和i
👋路径总和ii
👋从中序与后序遍历序列构造二叉树
👋从前序与中序遍历序列构造二叉树
👋最大二叉树

👋计算二叉树所有左叶子之和

leetcode题目链接
在这里插入图片描述

解题思路：这道题我们首先要清楚，什么是左叶子

左叶子：位于父节点的左子树，且自身没有左右节点

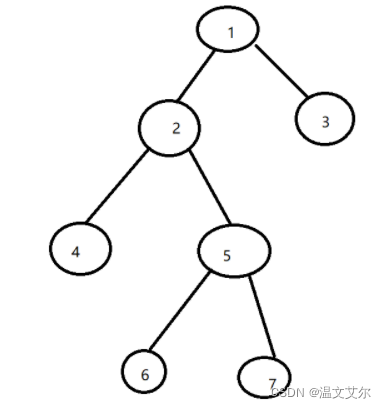
如下面这幅画（画的丑见谅0.0）

在这里插入图片描述

2就不是左叶子，虽然他没有子节点，但是他不在1节点的左边

清楚了什么是左叶子，我们就可以真正解决这道题，那么我们可以想到，某节点的左子树可能存在左叶子，它的
右子树也可能存在左叶子，它的左子树的左子树也可能存在左叶子

在这里插入图片描述

我们用深度优先搜索，后序遍历（左右中）判断就会比较方便，只需要一直向子树中递归就行

代码奉上

    public int sumOfLeftLeaves(TreeNode root) {
        if (root==null)return 0;
        int left = sumOfLeftLeaves(root.left);
        int right = sumOfLeftLeaves(root.right);

        int mid = 0;
        if (root.left!=null&&root.left.left==null&&root.left.right==null){
            mid=root.left.val;
        }
        return mid+left+right;
    }

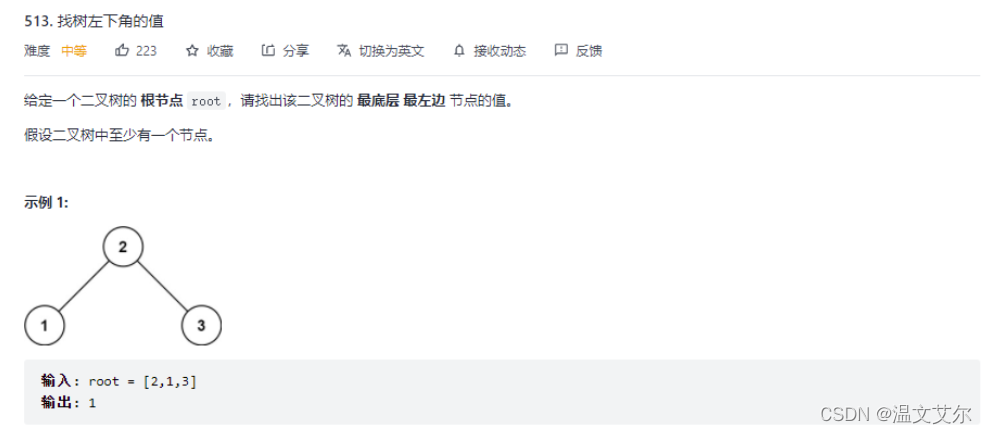
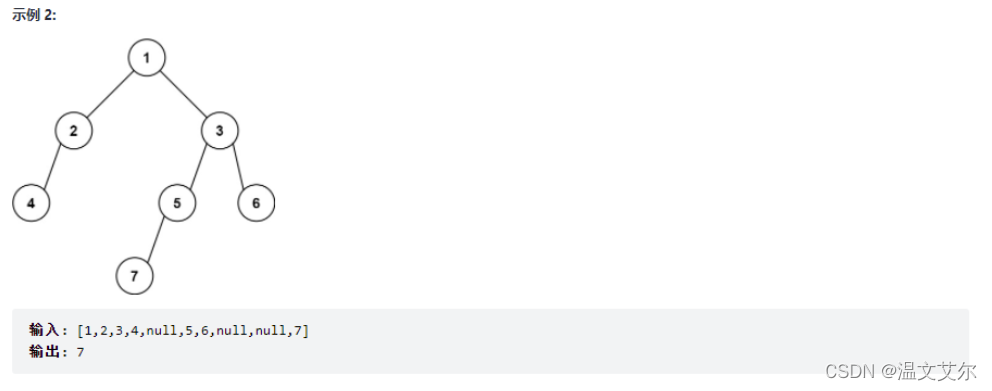
在这里插入图片描述

👋找树左下角的值

leetcode题目链接
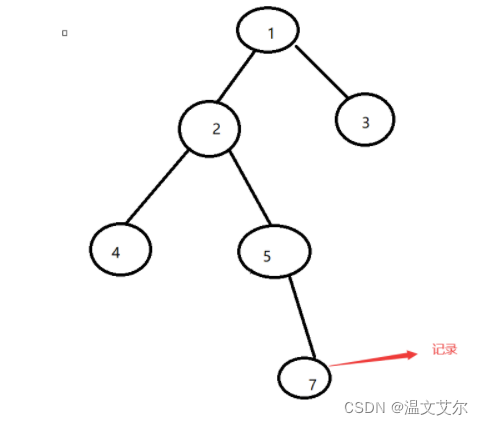
在这里插入图片描述

解题思路：本题使用层寻遍历最简单也最方便理解，因为只需要一层一层遍历然后统计最后一行的第一个数据就可以

在这里插入图片描述

    public int findBottomLeftValue(TreeNode root) {
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int left = 0;
        while (!queue.isEmpty()){
            int len = queue.size();
            for (int i=0;i<len;i++){
                TreeNode poll = queue.poll();
                if (i==0) left=poll.val;
                if (poll.left!=null) queue.offer(poll.left);
                if (poll.right!=null) queue.offer(poll.right);
            }
        }
        return left;
    }

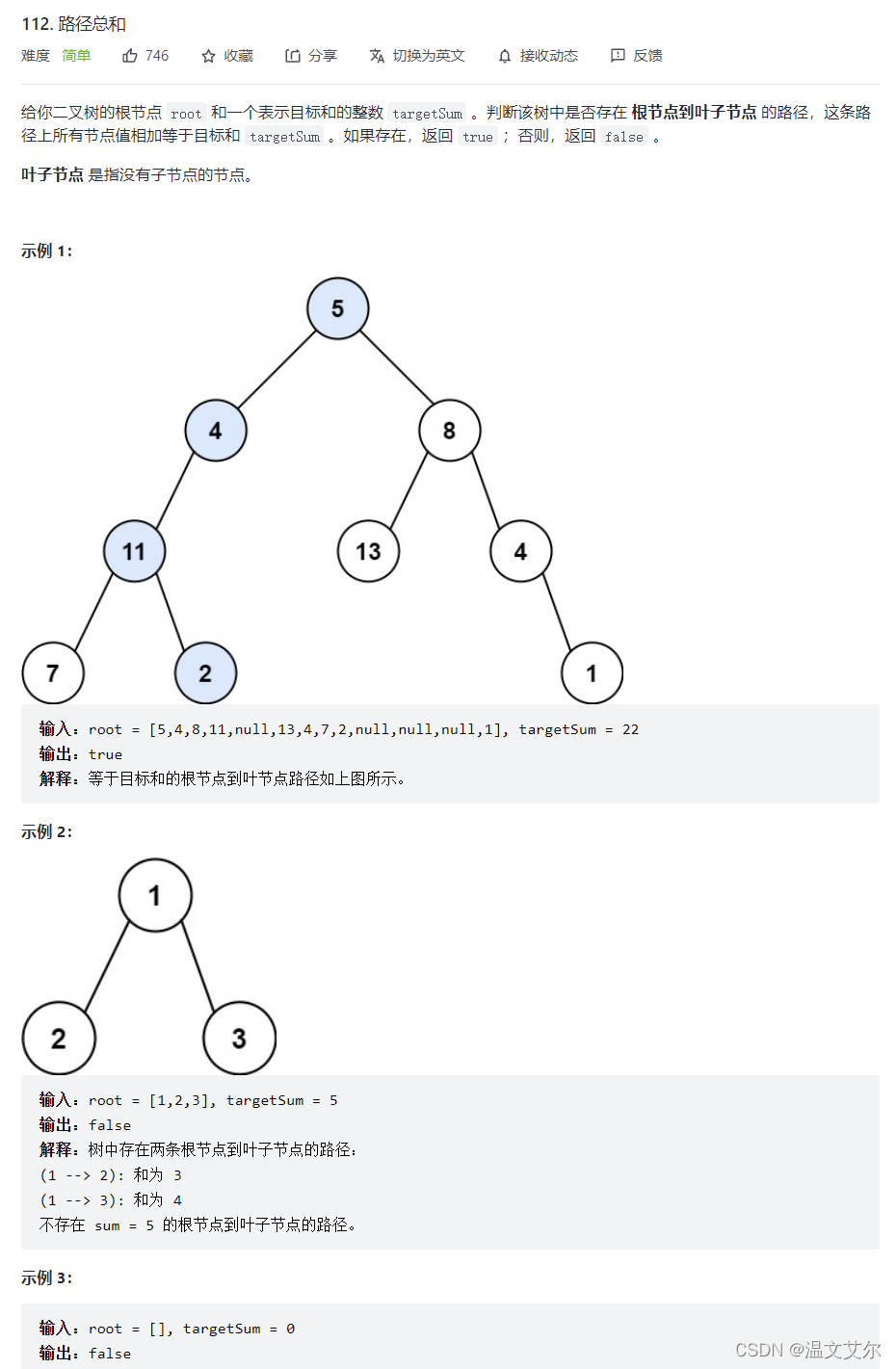
在这里插入图片描述

👋路径总和i

题目链接
在这里插入图片描述

题解思路：

深度优先搜索比较适合本题，我们遍历从根节点到叶子结点的路径，看看综合与targetSum是否相等，在进行递归的时候可以把每个节点的值都记录下来，如果不等的话就进行回溯

既然确定要使用递归，那么就必须确定以下三个要素

确定递归函数的参数和返回值
确定终止条件
确定单层递归的逻辑

第一个要素，我们可以确定，参数时肯定要有

根节点root，不然没办法递归了
有一个值count来记录路径的和，返回值的话，我们可以看到leetcode题目上返回值为boolean类型，我们的返回值也会是boolean类型
targetSum

第二个要素，终止条件肯定是到达根节点

路径的和与targetSum不相等，终止，进行回溯
路径的和与targetSum相等，终止，直接返回

第三个要素，如果有左子节点就向左递归，如果有右子节点就向右递归，记得回溯的时候把count减去未达标节点的val

    public boolean hasPathSum(TreeNode root, int targetSum) {
        if (root==null) return false;
        return check(root,root.val,targetSum);
    }

    private boolean check(TreeNode root, int count,int target) {
        if (root.left==null&&root.right==null&&count!=target){
            return false;
        }
        if (root.left==null&&root.right==null){
            return true;
        }
        if (root.left!=null){
            count+=root.left.val;
            if(check(root.left,count,target)) return true;
            count-=root.left.val;
        }
        if (root.right!=null){
            count+=root.right.val;
            if (check(root.right,count,target))return true;
            count-=root.right.val;
        }
        return false;
    }

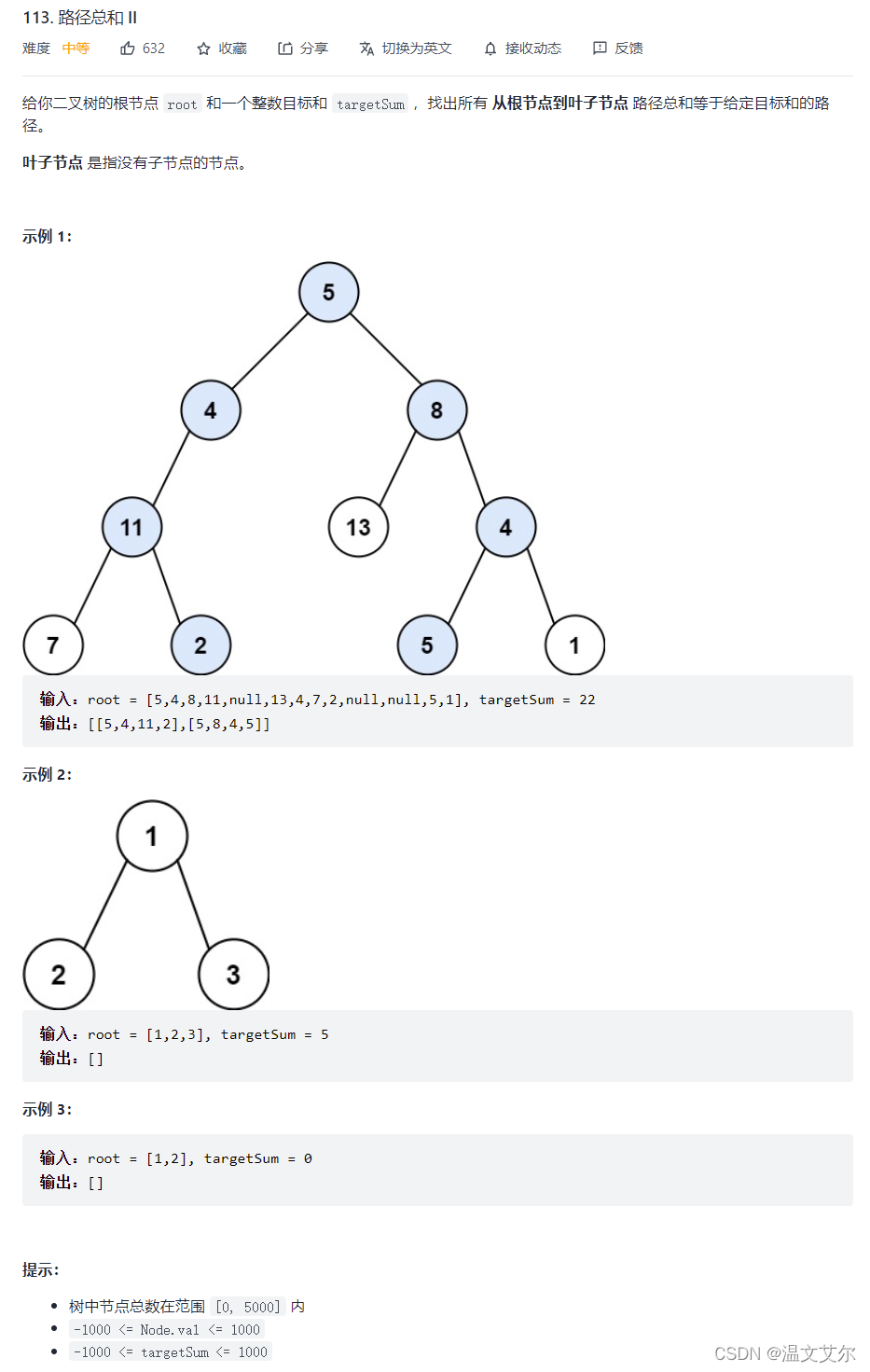
在这里插入图片描述

👋路径总和ii

leetcode题目链接
在这里插入图片描述

解题思路：

这题和上一题的模式是差不多的但是递归三要素却不一样，我们不仅需要判断值是否满足，还需要把所有符合条件的路径记录下来

我们重新规范一下本题的递归三要素

确定递归函数的参数和返回值
确定终止条件
确定单层递归的逻辑

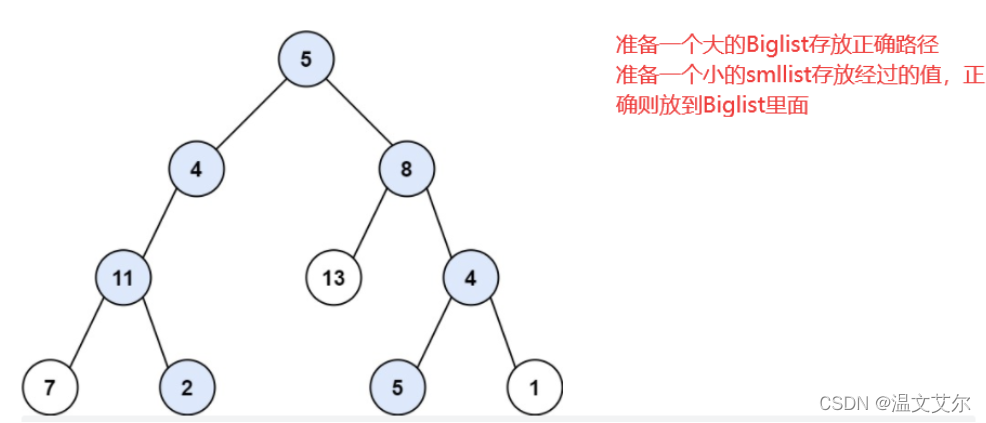
第一个要素，除了root,count,targetSum，我们还需要传进去一个集合Biglist用来保存所有正确的路径，还需要一个集合Smllist用来记录每次经过的节点值，递归不需要返回值

第二个要素，终止条件肯定是到达根节点

路径的和与targetSum不相等，终止，进行回溯
路径的和与targetSum相等，终止，将路径记录在集合中

第三个要素和上一题相同

在这里插入图片描述

    public List<List<Integer>> pathSum(TreeNode root, int targetSum) {
        List<List<Integer>> Biglist = new ArrayList<>();
        if (root==null)return Biglist;
        List<Integer> smllist = new ArrayList<>();
        check(root,targetSum,Biglist,smllist);
        return Biglist;
    }

    private void check(TreeNode root, int targetSum, List<List<Integer>> biglist, List<Integer> smllist) {
        smllist.add(root.val);
        if (root.left==null&&root.right==null){
            if (targetSum-root.val==0){
                biglist.add(new ArrayList<>(smllist));
            }else {
                return;
            }
        }

        if (root.left!=null){
            check(root.left,targetSum-root.val,biglist,smllist);
            smllist.remove(smllist.size()-1);
        }
        if (root.right!=null){
            check(root.right,targetSum-root.val,biglist,smllist);
            smllist.remove(smllist.size()-1);
        }
    }

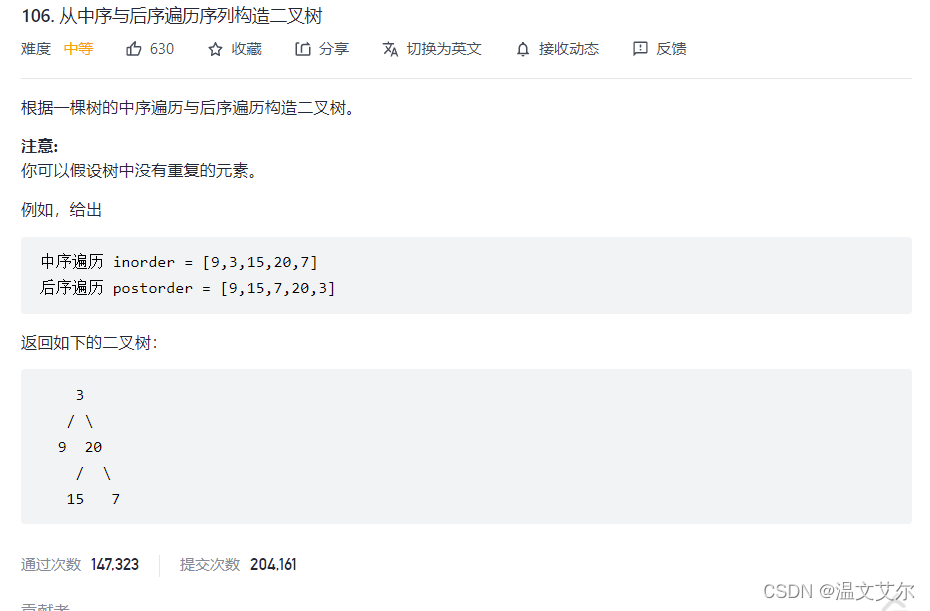
在这里插入图片描述

👋从中序与后序遍历序列构造二叉树

leetcode题目链接
在这里插入图片描述

题解思路：观察后序遍历，我们发现后序遍历数组的最后一个元素就是根节点n，而n在中序遍历的位置刚好将切割中序遍历数组，将其一分为二，n的左边为左子树，n的右边为右子树，然后进行递归

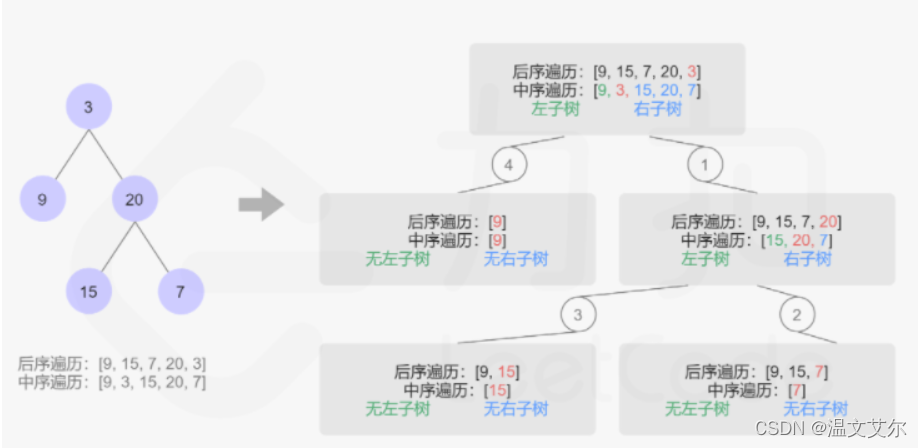
在这里插入图片描述
以中序遍历 inorder = [9,3,15,20,7] 后序遍历 postorder = [9,15,7,20,3] 为例

第一步找到3在inorder中的位置，位置为1
将inorder以索引1为分界点进行切割[9],[15,20,7]分别进行递归
当数组中只有一个元素时证明它是叶子结点，直接返回
当数组中有多个元素时例如[15,20,7]，以20在中序数组中的位置再次进行切割递归，直到找到叶子结点

    public Map<Integer,Integer> map = new TreeMap<>();
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        //放到map中方便寻找下标
        for (int i = 0; i < inorder.length; ++i) {
            map.put(inorder[i],i);
        }
        return Mybuild(inorder,0,inorder.length-1,postorder,0,postorder.length-1);
    }

    private TreeNode Mybuild(int[] inorder, int inLeft, int inRight, int[] postorder, int posLeft, int posRight) {
        if (inLeft>inRight){
            return null;
        }
        int index = map.get(postorder[posRight]);//获得后序遍历数组中节点在中序遍历中的位置

        TreeNode root = new TreeNode(postorder[posRight]);

        root.left = Mybuild(inorder,inLeft,index-1,postorder,posLeft,posLeft+(index-inLeft)-1);
        root.right = Mybuild(inorder,index+1,inRight,postorder,posLeft+(index-inLeft),posRight-1);

        return root;
    }

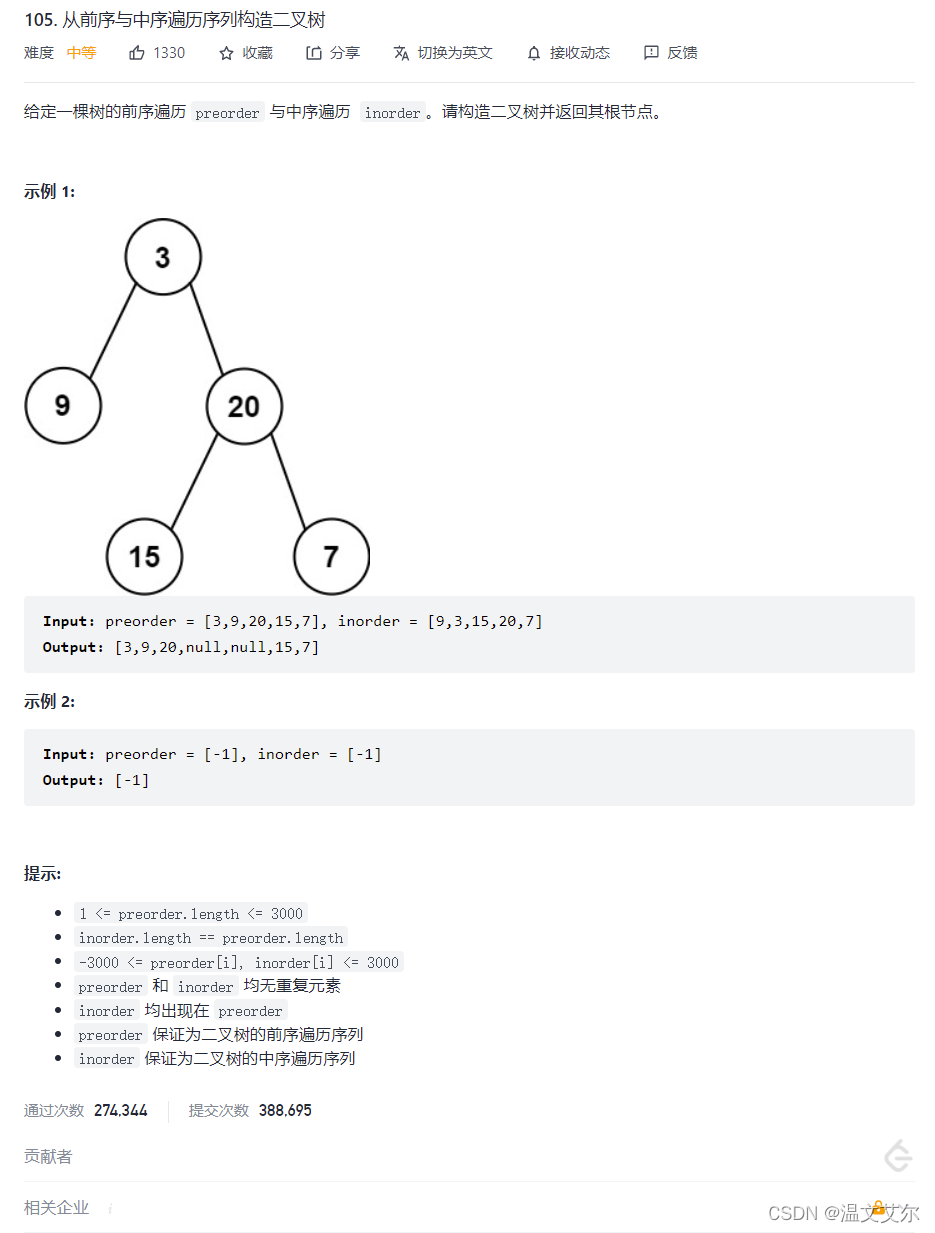
在这里插入图片描述

👋从前序与中序遍历序列构造二叉树

leetcode题目链接
在这里插入图片描述

解题思路：解题思路可以仿照第五题，我们发现前序遍历数组的第一个元素是中间节点，由此我们可以得到中间节点在中序遍历数组中的下标index，根据Index将中序遍历数组一分为二，左边即为左子树，右边就是右子树，进行递归

    public TreeNode buildTree(int[] preorder, int[] inorder) {
       return MyBuild(preorder,0,preorder.length-1,inorder,0,inorder.length-1);
    }

    private TreeNode MyBuild(int[] preorder, int preLeft, int preRight,int[] inorder, int inLeft, int inRight) {
        if (inLeft>inRight||preLeft>preRight){
            return null;
        }
        int idx = inLeft;

        //得到首节点下标
        int rootIndex = 0;
        for (int i=inLeft;i<=inRight;i++){
            if (preorder[preLeft]==inorder[i]){
                rootIndex=i;
                break;
            }
        }
        //创建首结点
        TreeNode root = new TreeNode(preorder[preLeft]);

        root.left=MyBuild(preorder,preLeft+1,preLeft+(rootIndex-inLeft),inorder,inLeft,rootIndex-1);
        root.right= MyBuild(preorder,preLeft+(rootIndex-inLeft)+1,preRight,inorder,rootIndex+1,inRight);

        return root;
    }

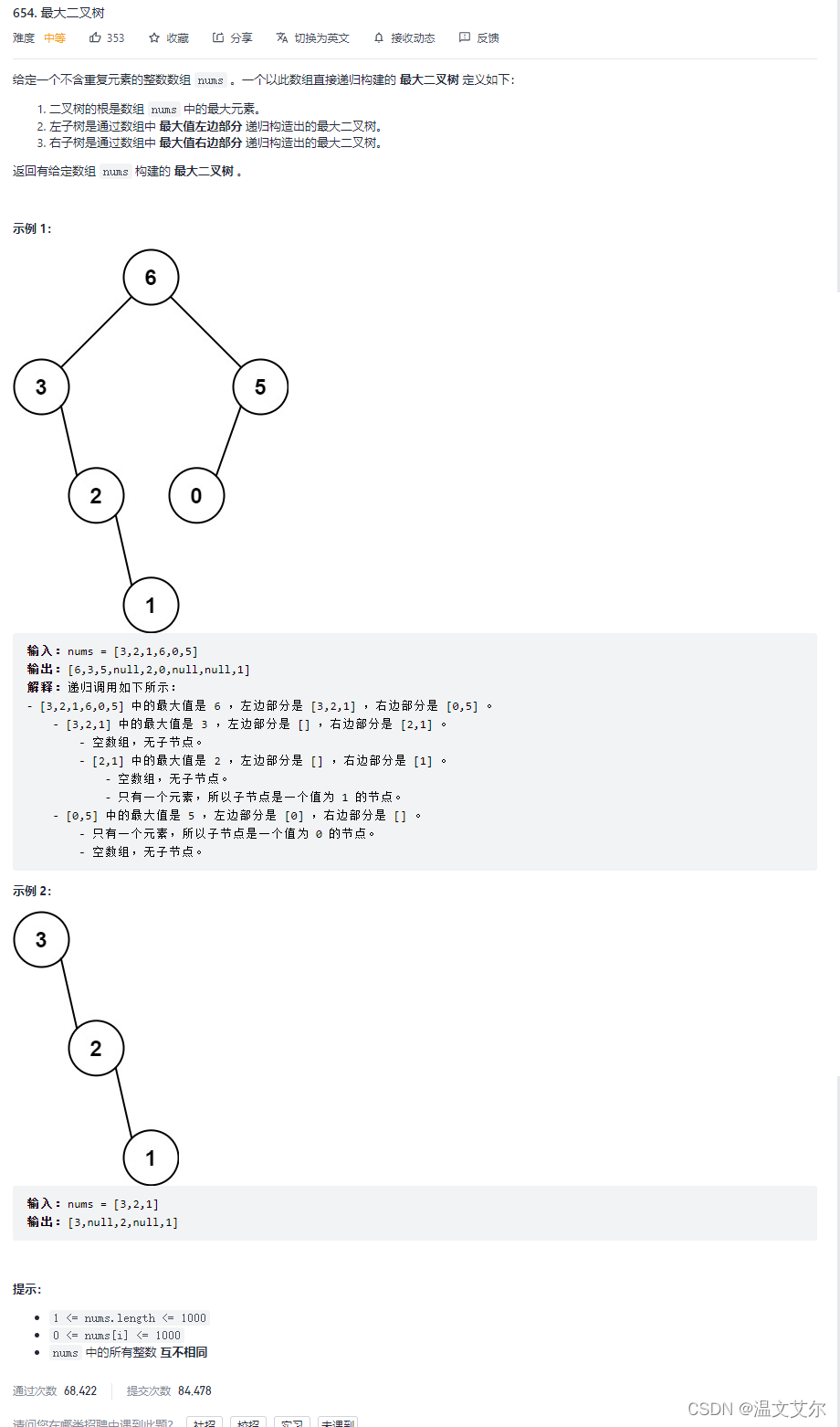
在这里插入图片描述

👋最大二叉树

leetcode题目链接
在这里插入图片描述

递归调用如下所示：

[3,2,1,6,0,5] 中的最大值是 6 ，左边部分是 [3,2,1] ，右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ，左边部分是 [] ，右边部分是 [2,1] 。
  - 空数组，无子节点。
  - [2,1] 中的最大值是 2 ，左边部分是 [] ，右边部分是 [1] 。
    - 空数组，无子节点。
    - 只有一个元素，所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ，左边部分是 [0] ，右边部分是 [] 。
  - 只有一个元素，所以子节点是一个值为 0 的节点。
  - 空数组，无子节点。

首先找到每组中的最大值n的下标index，以index为分界点，[left,index-1]为左子树,[index+1,right]为右子树，分别递归

    public TreeNode constructMaximumBinaryTree(int[] nums) {
        return buildBigTree(nums,0,nums.length-1);
    }

    private TreeNode buildBigTree(int[] nums, int left, int right) {
        if (left>right){
            return null;
        }

        //找出最大值
        int index = left;
        int max = nums[left];

        for (int i = left+1; i <=right; i++) {
            if (nums[i]>max){
                max=nums[i];
                index=i;
            }
        }
        //创建根节点
        TreeNode root = new TreeNode(max);

        root.left = buildBigTree(nums,left,index-1);//0 2
        root.right = buildBigTree(nums,index+1,right);//4 5

        return root;
    }

🙏亲爱的朋友，如果对你有帮助，给博主一个免费的点赞以示鼓励把QAQ☺

这里是温文艾尔の刷题学习之路
🙏作者水平欠佳，如果发现任何错误，欢迎批评指正
👋博客主页温文艾尔の学习小屋
👋更多文章请关注温文艾尔主页
👋超详细Leetcode刷题解析！
👋更多文章：
👋Leetcode刷题日记精选例题（附代码+链接）1
👋LeetCode刷题日记精选例题（附代码+链接）2
👋LeetCode刷题日记精选例题（附代码+链接）3
👋LeetCode刷题日记精选例题（附代码+链接）4
👋LeetCode刷题日记精选例题-双指针经典问题总结
👋LeetCode刷题日记精选例题（解析+代码+链接）5
👋11道精选经典LeetCode例题让你彻底搞懂二叉树的广度优先遍历
👋LeetCode刷题日记精选例题（附代码+链接）6