轨迹优化入门必备 — GPOPS-II

1. 简介

GPOPS-II (General Purpose Optimal Control Software II) 是佛罗里达大学 Anil V. Rao 教授课题组开发的一款通用最优控制与轨迹优化工具箱

GPOPS-II的最大特色是：

• 基于 hp 自适应伪谱法(hp-adaptive pseudospectral method)，能够灵活处理多阶段轨迹优化问题、提高轨迹优化问题求解精度
• 本质上是一个建模工具箱，用户只需要定义动力学方程、边界条件、目标函数，就能自动生成并求解非线性规划 (NLP) 问题。
• 底层调用 SNOPT 或 IPOPT 作为求解器 (后续会写介绍 IPOPT 的文章)

需要注意：

• 第一代GPOPS和早期GPOPS-II 有部分免费资源
• 最新版本（>=2.5）属于商业软件，大陆地区目前无法直接获得

官方网站：https://gpops2.com/

2. 快速入门

最好的学习路径就是 examples 文件夹，里面包含经典轨迹优化案例
这里以 Moon Lander Problem (月球软着陆问题) 为例

目标函数：$J={\int }_0^{t_f}u\left(t\right)dt$

运动学方程：$\begin{array}{l}h\left(t\right)=v\left(t\right)\\ v\left(t\right)=-g+u\left(t\right)\end{array}$

边界条件：$\begin{array}{l}h\left(0\right)=h_0,h\left(t_f\right)=0\\ v\left(0\right)=v_0,v\left(t_f\right)=0\end{array}$

对应的GPOPS-II程序包含3个主要文件:

1. moonlanderMain.m：主函数，定义问题结构与求解设置
2. moonlanderContinuous.m：动力学函数，描述飞行器状态
3. moonlanderEndpoint.m：终端函数，定义目标函数与终端条件

2.1 主函数：moonlanderMain.m

在主函数中，主要完成以下工作：选择 NLP 求解器、选择初始网格设置、定义变量的边界条件、给定初值与初始猜测、调用求解器求解(例如IPOPT)
轨迹优化入门必备 — IPOPT
可以看到，GPOPS-II 的建模流程和 AMPL / Pyomo 类似，但接口完全嵌入 MATLAB，非常直观

%----------------------- Moon-Lander Problem -----------------------------%
clear all; close all; clc;

% 求解选项设置
setup.name = 'moonlander';

setup.functions.endpoint   = @moonlanderEndpoint;
setup.functions.continuous = @moonlanderContinuous;

setup.nlp.solver = 'ipopt';
setup.derivatives.supplier = 'sparseCD';
setup.derivatives.derivativelevel = 'second';
setup.scales.method = 'automatic-bounds';

setup.method = 'RPMintegration';

% 网格配置 (hp自适应)
setup.mesh.method = 'hp';
setup.mesh.tolerance = 1e-9; % default 1e-3
N = 1;
setup.mesh.phase.colpoints = 10*ones(1,N);
setup.mesh.phase.fraction   = ones(1,N)/N;

% 问题参数设置
h0 = 10; hf = 0;
v0 = -2; vf = 0;

hmin = 0; hmax =  20;
vmin = -10; vmax =  10;
umin = 0; umax = 3;
t0min = 0; t0max = 0;
tfmin = 0; tfmax = 200;

% 初始状态和终端状态
setup.bounds.phase.initialstate.lower = [h0, v0];
setup.bounds.phase.initialstate.upper = [h0, v0];
setup.bounds.phase.state.lower = [hmin, vmin];
setup.bounds.phase.state.upper = [hmax, vmax];
setup.bounds.phase.finalstate.lower = [hf, vf];
setup.bounds.phase.finalstate.upper = [hf, vf];
% 控制约束
setup.bounds.phase.control.lower = [umin];
setup.bounds.phase.control.upper = [umax];
% 积分约束
setup.bounds.phase.integral.lower = [-100];
setup.bounds.phase.integral.upper = [100];
% 时间约束
setup.bounds.phase.initialtime.lower = t0min;
setup.bounds.phase.initialtime.upper = t0max;
setup.bounds.phase.finaltime.lower = tfmin;
setup.bounds.phase.finaltime.upper = tfmax;

% 初始猜测
h_guess = [h0; hf];
v_guess = [v0; vf];
u_guess = [umin; umin];
t_guess = [t0min; 5];
setup.guess.phase.state   = [h_guess, v_guess];
setup.guess.phase.control = [u_guess];
setup.guess.phase.time    = [t_guess];
setup.guess.phase.integral = 10;

setup.auxdata.g = 1.6;

% 调用求解器
output = gpops2(setup);
solution = output.result.solution;

2.2 动力学函数：moonlanderContinuous.m

该文件定义状态的微分方程，即系统的动力学约束

function phaseout = moonlanderContinuous(input)
g = input.auxdata.g;

t = input.phase.time;
h = input.phase.state(:,1);
v = input.phase.state(:,2);
u = input.phase.control(:,1);

dh = v;
dv = -g + u;

phaseout.dynamics = [dh, dv];
phaseout.integrand = u;

2.3 终端函数：moonlanderEndpoint.m

该文件定义目标函数和终端条件

在本问题中：

• 终端条件已在 main 文件的 bounds 中定义
• 这里仅定义目标函数，即推力积分最小化

function output = moonlanderEndpoint(input)
Qu = input.phase.integral;

output.objective = Qu;

最终求解结果如下

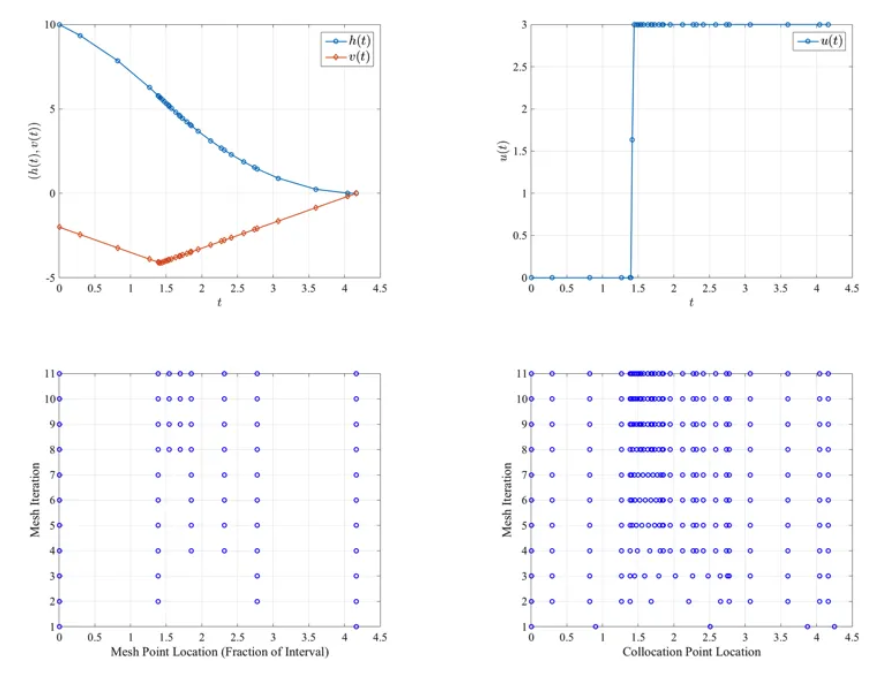
3. 个人经验与踩坑

• 上手难度：建模相对简单，关键是清晰写出状态方程、边界条件
• 求解收敛性：初值和初始网格点对收敛极其关键；先用较松的 mesh调试，再逐步收紧
• 约束建模：要特别注意边界条件的合理性，否则很容易导致不可行解
• IPOPT 报错问题：在 MATLAB 下直接调用 IPOPT 可能报错 Invalid MEX-file error；推荐安装 OPTI Toolbox 来解决 MEX 接口问题

4. 总结

GPOPS-II 是一个非常强大的轨迹优化工具：

• hp-adaptive pseudospectral method 保证了高精度与高效率
• 适合处理多阶段、复杂约束的航天/航空/机器人轨迹优化问题
• 对新手友好，但要真正玩转，需要对最优控制建模和数值优化有一定理解

欢迎订阅，微信公众号同名
公众号文章