一、拉普拉斯变换的定义式
当函数f(t)满足狄里赫利条件时,便可构成一对傅里叶变换式


考虑到在实际问题中遇到的总是因果信号,令信号起始时刻为零,于是在t<0的时间范围内f(t)等于零,这样,正变换表示式的积分下限可从零开始
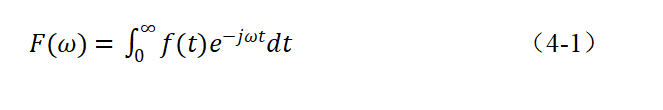
但仍包含有
与
两部分分量,因此逆变换式的积分限不改变。再从狄里赫利条件考虑,在此条件之中,绝对可积的要求限制了某些增长信号如
傅里叶变换的存在,而对于阶跃信号、周期信号虽未受此约束,但其变换式中出现冲激函数
,为使更多的函数存在变换,并简化某些变换形式或运算过程,引入一个衰减因子
(
为任意实数)使它与f(t)相乘,于是
得以收敛,绝对可积条件就容易满足。按此原理,写出
的傅里叶变换

将式中用符号s代替,令
,式(4-2)遂可写作

下面由傅里叶逆变换表示式求,再寻找由F(s)求f(t)的一般表示式

等式两边各乘以,因为它不是
的函数,可放到积分号内,于是得到

已知,所以
,若
为选定之常量,则
,以此代入式(4-5),并相应地改变积分上下限,得到

式(4-3)和式(4-6)就是一对拉普拉斯变换式(或称拉氏变换对)。两式中的f(t)称为“原函数”,F(s)称为“象函数”。已知f(t)求F(s)可由式(4-3)取得拉氏变换。反之,利用式(4 - 6)由F(s)求f(t)时称为逆拉氏变换(或拉氏逆变换)。常用记号![]() 表示取拉氏变换,以记号
表示取拉氏变换,以记号 ![]() 表示取拉氏逆变换。于是,式(4 - 3)和式(4 - 6)可分别写作
表示取拉氏逆变换。于是,式(4 - 3)和式(4 - 6)可分别写作
拉氏正变换:
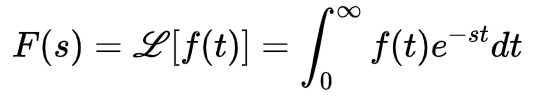
拉氏逆变换:

二、常用函数的拉普拉斯变换
| 序号 | f(t) (t>0) | F(s) |
|---|---|---|
| 1 | 冲激函数 | 1 |
| 2 | 阶跃函数 | |
| 3 | ||
| 4 | ||
| 5 | ||
| 6 | ||
| 7 | ||
| 8 | ||
| 9 | ||
| 10 | ||
| 11 | ||
| 12 | ||
| 13 | ||
| 14 |
三、拉普拉斯变换的基本性质
| 序号 | 名称 | 结论 |
|---|---|---|
| 1 | 线性(叠加) | |
| 2 | 对t微分 | |
| 3 | 对t积分 | |
| 4 | 延时(时域平移) | |
| 5 | s域平移 | |
| 6 | 尺度变换 | |
| 7 | 初值 | |
| 8 | 终值 | |
| 9 | 卷积 | |
| 10 | 相乘 | |
| 11 | 对s微分 | |
| 12 | 对s积分 |
四、使用Matlab计算拉氏正变换和逆变换
在Matlab中,我们可以使用laplace函数计算拉氏正变换,ilaplace函数计算拉氏逆变换
例1 求的拉氏变换
解析:这道题比较简单,直接套公式()即可
代码如下:
syms t;%定义符号变量
f = exp(-t)*sin(2*t);%f(t)表达式
F = laplace(f)%求f的拉氏变换运行结果:

例2 求的单边拉氏变换
解析:由于乘以了一个
,已经是一个因果信号了,所以在求积分时不用再管
了,求出积分后,再代入公式(
)
代码如下:
syms t tau;%定义符号变量
f = int((2*tau+1)*heaviside(tau), tau, [0,t]);%int函数用于求积分
F = simplify(laplace(f))%simplify函数用于化简运行结果:

例3 求的拉氏逆变换
解析:可以先将其因式分解,然后再部分分式展开,使用留数法计算待定系数后,再根据包含共轭复数极点的拉氏逆变换的公式:
即可求出最终结果
具体步骤如下:
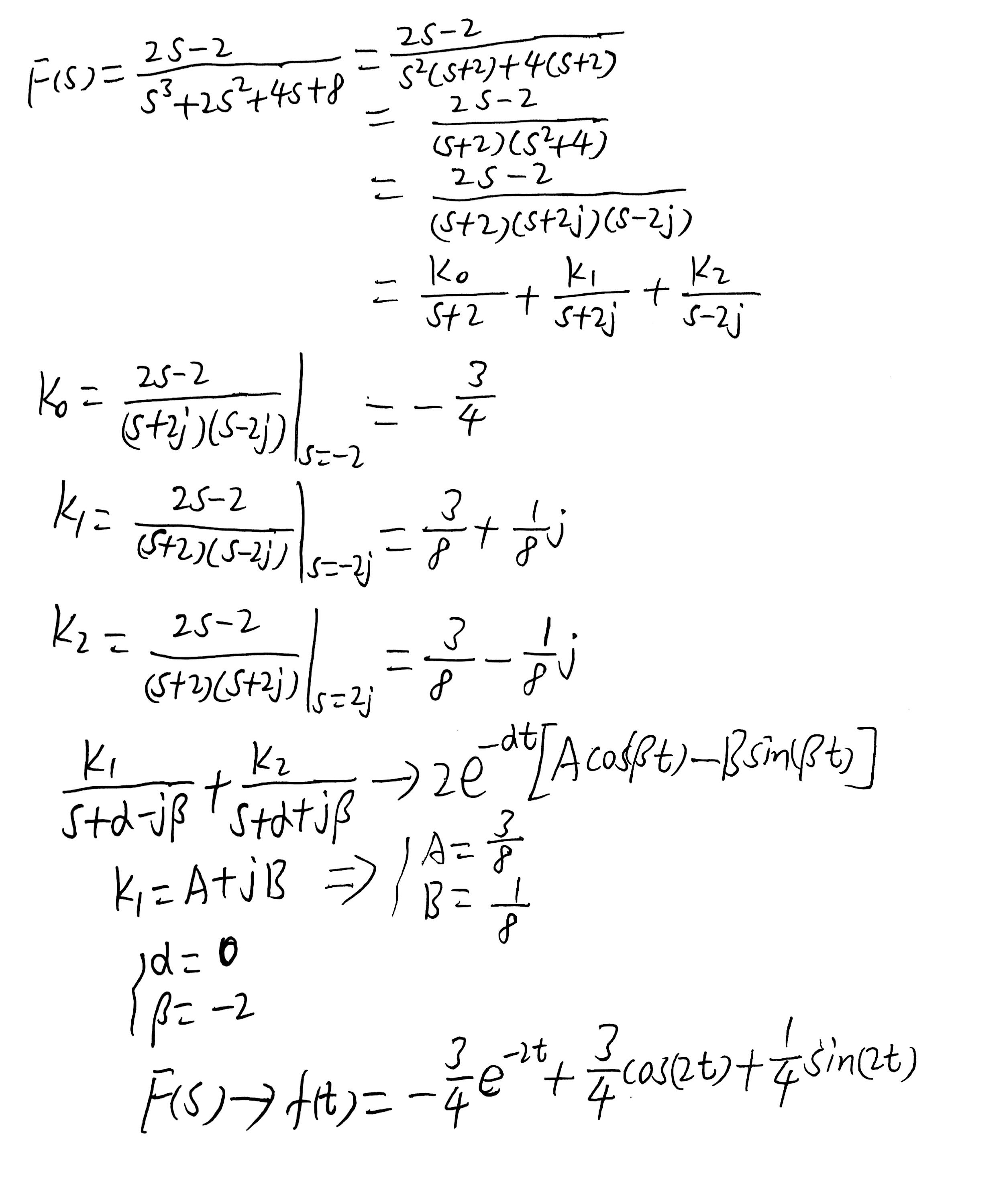
代码如下:
syms s;%定义符号变量
F = (2*s-2)/(s^3+2*s^2+4*s+8);%F(s)表达式
f = ilaplace(F) %求F的拉氏逆变换
ezplot(f);%画出f(t)的图像运行结果:


例4 求的拉氏逆变换
解析:只需将象函数部分分式分解,再代入公式()(
)
代码如下:
syms s;%定义符号变量s
F = 2/(s^3+2*s);
f = ilaplace(F)%计算F(s)的拉氏逆变换
ezplot(f);%画出f(t)的图像运行结果:

























 5119
5119

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








