回归（Regression)

w,b都是参数

从函数集中找出最好的函数（使得损失函数的值最小）

arg max f(x): 当f(x)取最大值时，x的取值

怎么找出一对w,b是得loss值最小？那就是梯度下降的方法

梯度为负 右走，梯度为正 左走

梯度的本意是一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大（为该梯度的模）。

找出了最好的w,b

 

但是这个函数预测的不准确，则选择其他的模型

 二次式

三次式

四次式

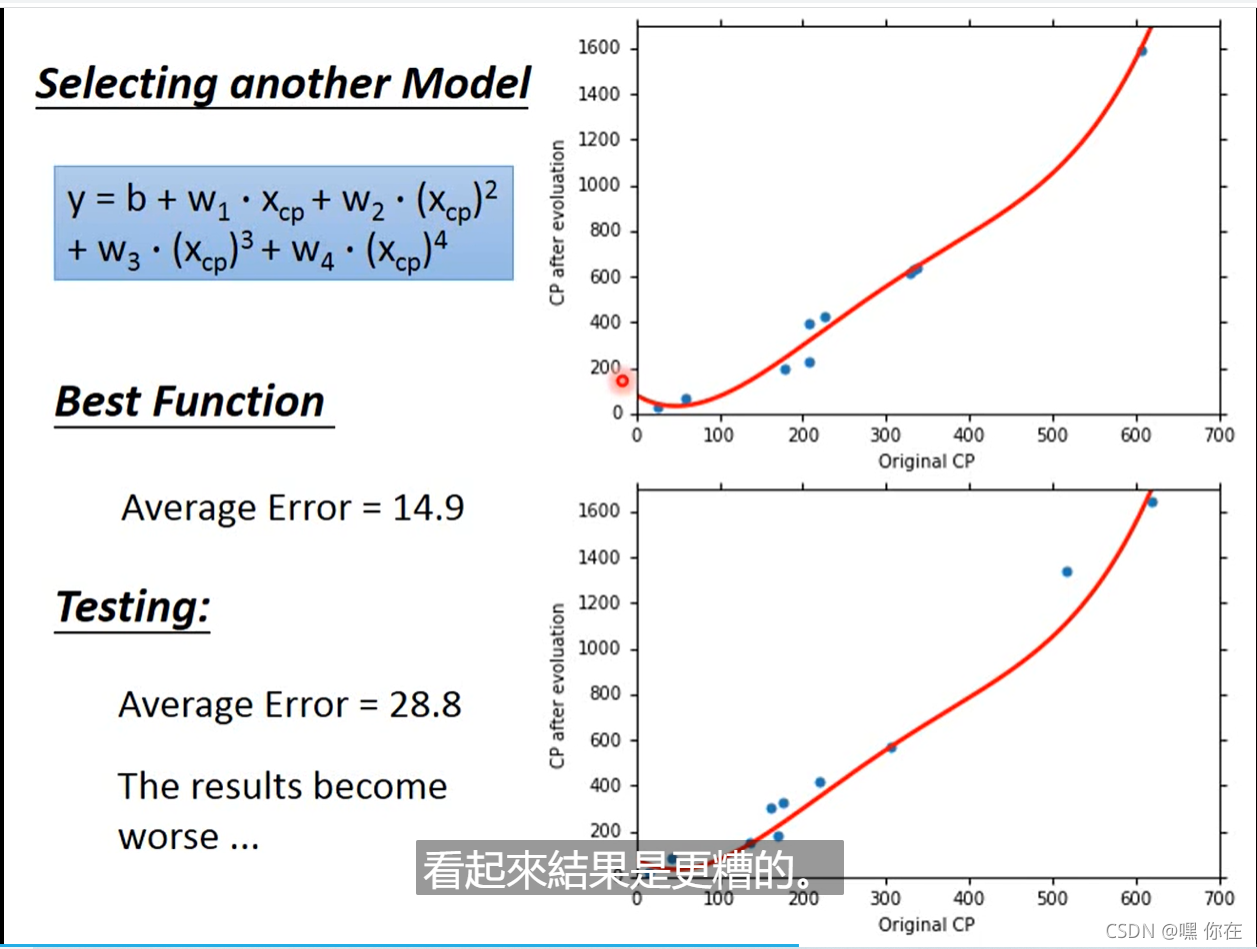
五次式

 Overfitting(过拟合)：

1.过拟合是指为了得到一致假设而使假设变得过度严格。避免过拟合是分类器设计中的一个核心任务。通常采用增大数据量和测试样本集的方法对分类器性能进行评价

2. 一个假设在训练数据上能够获得比其他假设更好的拟合， 但是在训练数据外的数据集上却不能很 地拟合数据，此时认为这个假设出现了过拟合的现象。出现这种现象的主要原因是训练数据中存在噪音或者训练数据太少。

 当形象因素较多时，需要重新构造函数（受动物种类影响）

其他的影响因素

 怎么解决呢？把所有的影响因素都考虑，塞进一个函数里面（如下图所示）

 我们发现，Testing data error 特别大。怎么解决呢？那就是下面的规范化（重新定义 loss function）

怎么解决过拟合问题？

1.方法一：尽量减少选取变量的数量

具体而言，我们可以人工检查每一项变量，并以此来确定哪些变量更为重要，然后，保留那些更为重要的特征变量。至于，哪些变量应该舍弃，我们以后在讨论，这会涉及到模型选择算法，这种算法是可以自动选择采用哪些特征变量，自动舍弃不需要的变量。这类做法非常有效，但是其缺点是当你舍弃一部分特征变量时，你也舍弃了问题中的一些信息。例如，也许所有的特征变量对于预测房价都是有用的，我们实际上并不想舍弃一些信息或者说舍弃这些特征变量。

2.方法二：Regularization（规范化，正则化）

正则化中我们将保留所有的特征变量，但是会减小特征变量的数量级（参数数值的大小θ(j)）。

这个方法非常有效，当我们有很多特征变量时，其中每一个变量都能对预测产生一点影响。正如我们在房价预测的例子中看到的那样，我们可以有很多特征变量，其中每一个变量都是有用的，因此我们不希望把它们删掉，这就导致了正则化概念的发生。

在正则化线性回归中，如果正则化参数值 λ 被设定为非常大，那么将会发生什么呢？

我们将会非常大地惩罚参数θ1 θ2 θ3 θ4 … 也就是说，我们最终惩罚θ1 θ2 θ3 θ4 …  在一个非常大的程度，那么我们会使所有这些参数接近于零。就会得到一个更平滑的曲线（不一定是二次函数）

  

值越大代表考虑smooth的那个Regularization那一项的影响力越大。function越平滑，在越少trainning data上的error越大。值越大 ，越倾向考虑w本来的值,考虑的trainning data 的error越少