Gradient Descent专题

vector 向量 

gradient 就是一个 vector

那么learning rate需要小心的调，learning rate 可以想象成走的步伐大小

Gradient Descent tip1:learning rate

但是调learning rate非常的麻烦，有没有自动调节learning rate的方法？

通常，learning rate随着参数的update 会越来越小。因为起始点的时候离目标比较远，步伐可以大点，但是随着离目标点越来越近，步伐需要变得小一点。

learning rate 的设法如上图

 

但是我们发现一个现象，本来应该是随着gradient的增大，我们的学习率是希望增大的，也就是图中的gt；但是与此同时随着gradient的增大，我们的分母是在逐渐增大，也就对整体学习率是减少的，这是为什么呢？

这是因为随着我们更新次数的增大，我们是希望我们的学习率越来越慢。因为我们认为在学习率的最初阶段，我们是距离损失函数最优解很远的，随着更新的次数的增多，我们认为越来越接近最优解，于是学习速率也随之变慢。

当参数update的次数越多的时候，learning rate就越小，但是这样是不够的，我们应该因材施教。（这种情况 learning rate是一样的）

 每个不同的参数都给一个不同的learning rate.有很多的小技巧解决这个问题，最容易的是Adagrad（自适应梯度算法）

 Adagrad是解决不同参数应该使用不同的更新速率的问题。（一个参数分配一个learning rate，一个参数一个参数的考虑）

root mean square(均方根):将N个项的平方和除以N后开平方的结果，即均方根的结果。

Adagrad自适应地为各个参数分配不同学习率的算法。其公式如下：

 例子：

怎么解释上图的式子？

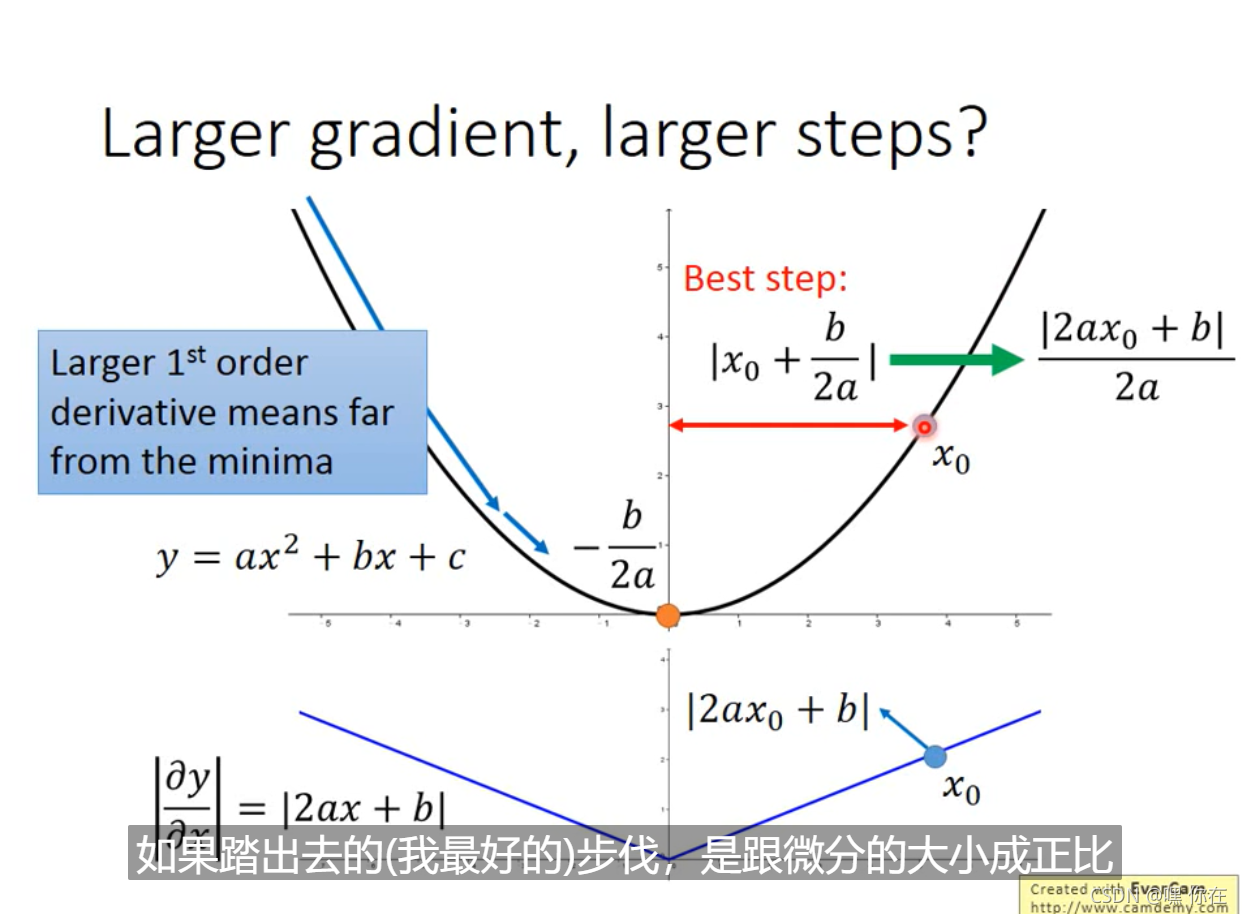
上图是针对一个参数的，若有两个参数呢？

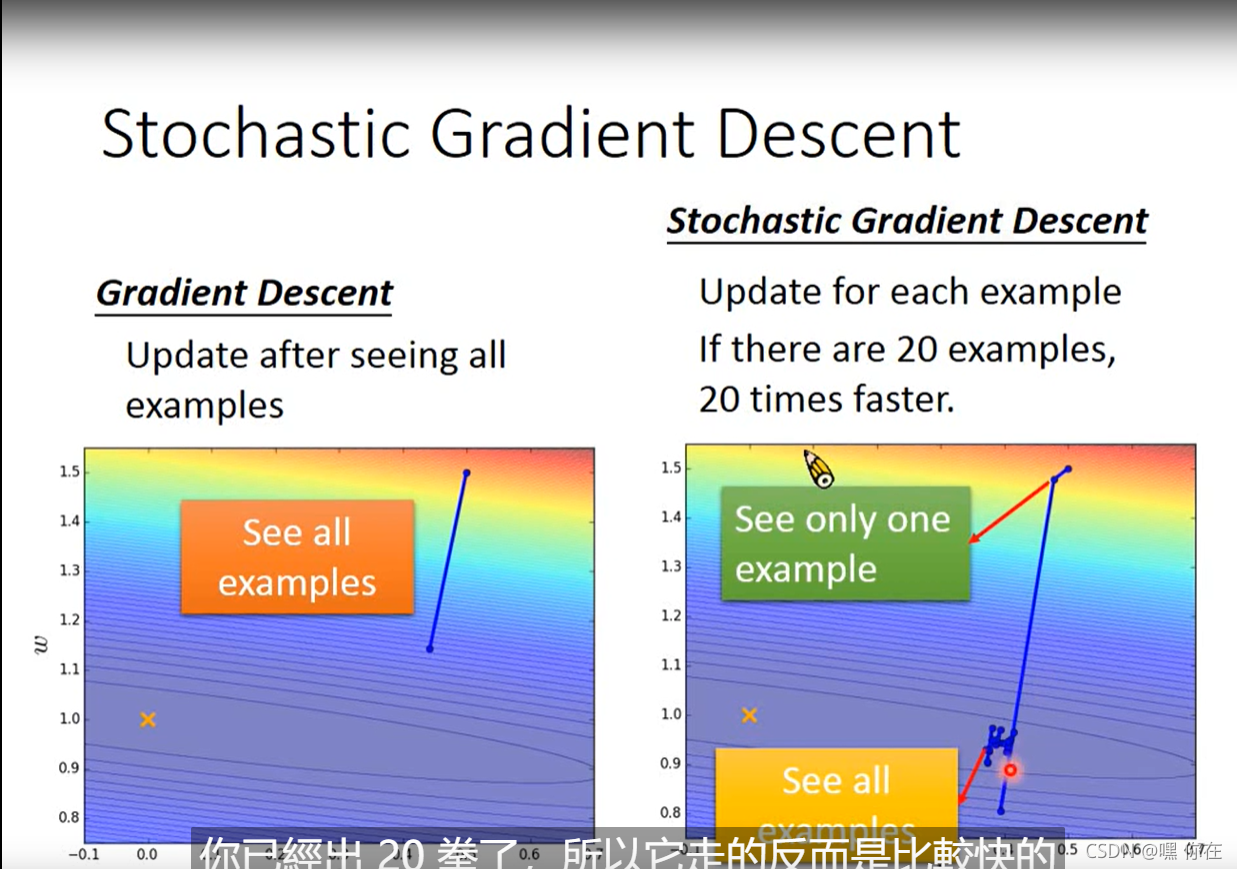
第二个tips:stochastic Gradient Descent 随机的

 第三个tips: Feature Scaling 特征放缩

 为什么这样做呢？

 对w1做微分 值较小，在w1方向是比较平滑的。

对于左图来说，自适应梯度是很好的，learning rate 是不一样的。对于右图来说，是朝着圆心走的，learning rate可以是一个。

怎样来收缩特征呢？

standard deviation 标准差