一、KNN定义
k k k近邻（ k − N e a r e s t N e i g h b o r ， 简 称 k N N k-Nearest Neighbor，简称kNN k−NearestNeighbor，简称kNN）学习是一种有监督学习方法。
k k k近邻：可以用于分类任务中，也可以用于回归中。
\qquad 在分类任务常采用“投票法”，即选择k个样本中出现最多的类别作为测试样本所属的类别；
\qquad 在回归任务中采用“平均法”，即将 k k k个样本的实际输出的平均值作为测试样本的输出结果。
二、KNN工作机制
\qquad
工作机制：给定测试样本数据集，基于某种距离度量找训练集中与其最靠近的
k
k
k个训练样本，然后基于这
k
k
k个邻居的信息来进行预测。
\qquad
图示：
当
k
=
1
k=1
k=1时，属于类别1
当
k
=
3
k=3
k=3时，属于类别2
当
k
=
5
k=5
k=5时，属于类别1
\qquad 从结果中可以看出， k k k是一个重要的参数， k k k的取值不同，会导致不同的分类结果。
\qquad 具体流程如下：
计算已知类别的数据集中的点与测试样本点之间的距离；
将计算的结果进行升序排列；
按照选取的 k k k，取出排序列表中前 k k k个样本点；
统计前 k k k个样本点所属的类别，统计类别出现的频率；
将出现频率最高的类别作为当前测试样本点的预测结果。
三、距离度量
闵可夫斯基距离（Minkowski distance）
欧式距离（Euclidean distance）
曼哈顿距离（Manhattan distance）
1.闵可夫斯基距离
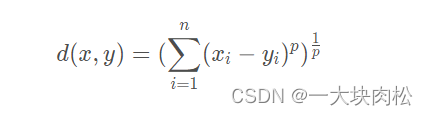
2.欧式距离
当 p = 2 p=2 p=2时，闵可夫斯基距离即是欧式距离
3.曼哈顿距离
当 p = 1 p=1 p=1时，闵可夫斯基距离即是曼哈顿距离
扫一扫
2423
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
