OpenCV-22高斯滤波

一、高斯函数的基础

要理解高斯滤波首先要直到什么是高斯函数，高斯函数是符合高斯分布的（也叫正态分布）的数据的概率密度函数。

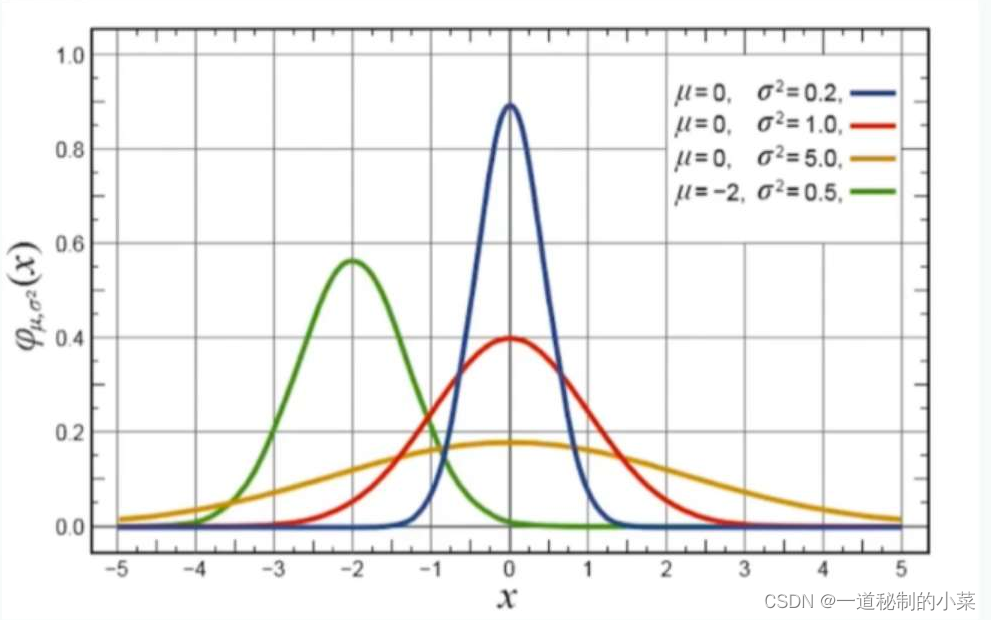
 高斯函数的特点是以x轴某一点（这一点称为均值）为对称轴，越靠近中心数据发生的概率越高，最终形成一个两边平缓，中间陡峭的钟型（有的地方也叫帽子）图形。

高斯函数的一般形式：以（0，0）和（0，0，0）为中点：

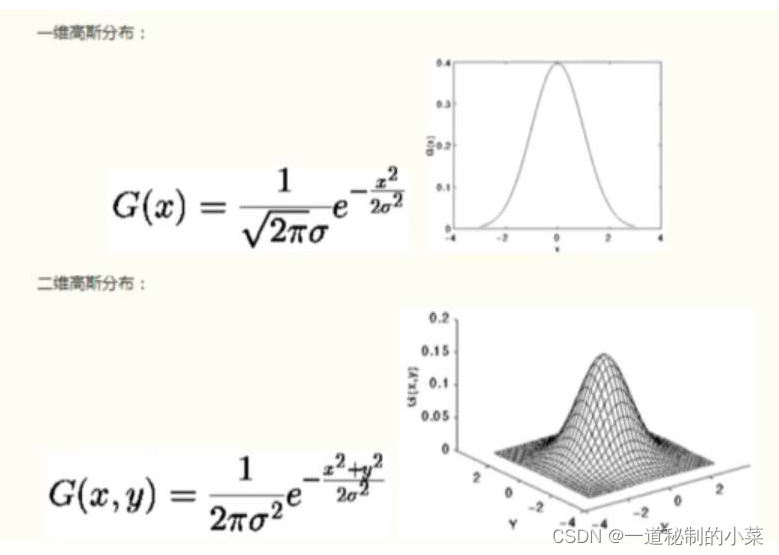
高斯滤波就是使用符合高斯分布的卷积核对图片进行卷积操作，所以高斯滤波的重点是如何计算符合高斯分布的卷积核，即高斯模板：

假设中心点的坐标为（0，0），那么取距离它最近的8个坐标，为了计算，需要设定  = 1.5，则模糊半径为1的高斯模板就如下所示：

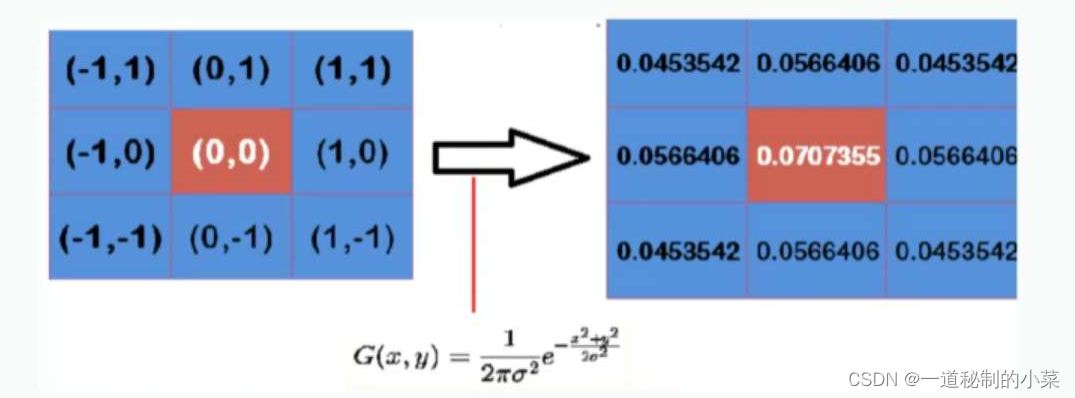
我们可以观察到越靠近中心值，数值越大，越边缘的数值越小，符合高斯分布的特点。

通过高斯函数计算得到的是概率函数密度， 所以我们还有确保着九个点加起来为1，这9个点的权重总和等于0.478