微分方程
需补齐:微分方程解性质和结构
概念
微分方程的两个组成概念:
1.方程
2.含有未知数的导数(微分)
通解
如果微分方程的解中含有独立常数个数等于微分方程的阶数,则该解称为微分方程的通解,独立常数是不会因为恒等变形而消去的常数
初始条件和特解
能够确定通解中常数的条件就是初始条件,比如y(x0)=a0,y’(x0)=a1,y(x0)(n-1)=an-1,确定了通解的常数后,解就成了特解
一、一阶微分方程
1.可分离变量型
可分离变量型
情况一
能写成y′=f(x)⋅g(y)y'=f(x)\cdot g(y)y′=f(x)⋅g(y)的,分离变量写成dyg(y)=f(x)dx\frac{dy}{g(y)}=f(x)dxg(y)dy=f(x)dx然后两边积分
情况二
能写成y′=f(ax+by+c)y' = f(ax+by+c)y′=f(ax+by+c)的
- 换元:令u=ax+by+c⇒u′=a+by′(x)u=ax+by+c\Rightarrow u'=a+by'(x)u=ax+by+c⇒u′=a+by′(x)
- 分离变量写成:dua+bf(u)=dx\frac{du}{a+bf(u)} =dxa+bf(u)du=dx
- 两边积分得出∫dua+bf(u)=∫dx\int\frac{du}{a+bf(u)} = \int dx∫a+bf(u)du=∫dx
齐次型
情况一
能写成y′=f(yx)y'=f(\frac{y}{x})y′=f(xy)的
- 令yx=u\frac{y}{x}=uxy=u换元
- 分离变量,也就是y=ux⇒dydx=u+xdudxy=ux\Rightarrow \frac{dy}{dx}=u+x\frac{du}{dx}y=ux⇒dxdy=u+xdxdu
- 由此可得出原方程为xdudx+u=f(u)⇒duf(u)−u=dyyx\frac{du}{dx}+u=f(u)\Rightarrow \frac{du}{f(u)-u}=\frac{dy}{y}xdxdu+u=f(u)⇒f(u)−udu=ydy
- 两边同时积分得
情况二
能写成1y′=f(xy)\frac{1}{y'}=f(\frac{x}{y})y′1=f(yx)的
- 令xy=u\frac{x}{y}=uyx=u换元
- 分离变量,也就是x=uy⇒dxdu=u+ydudyx=uy\Rightarrow \frac{dx}{du}=u+y\frac{du}{dy}x=uy⇒dudx=u+ydydu
- 由此可得出原方程为ydudy+u=f(u)⇒duf(u)−u=dyyy\frac{du}{dy}+u=f(u)\Rightarrow \frac{du}{f(u)-u}=\frac{dy}{y}ydydu+u=f(u)⇒f(u)−udu=ydy
- 两边同时积分得
一阶线性型
能写成y′+p(x)y=q(x)y'+p(x)y=q(x)y′+p(x)y=q(x)的情形:
- 直接使用公式法:y=e−∫p(x)dx[∫e∫p(x)dxq(x)dx+C]y=e^{-\int p(x)dx}[\int e^{\int p(x)dx}q(x)dx+C]y=e−∫p(x)dx[∫e∫p(x)dxq(x)dx+C]
TIPS:部分微分方程可以通过换元得到一阶线性型
二、二阶可降阶微分方程
y′′=f(x,y′)y''=f(x,y')y′′=f(x,y′)情形(缺y)
- 缺少y则令y′=py'=py′=p,y′′=p′y''=p'y′′=p′,并且将原方程变换为dpdx=f(x,p)\frac{dp}{dx}=f(x,p)dxdp=f(x,p)
- 求得通解y′=p=g(x,C1)y'=p=g(x,C_1)y′=p=g(x,C1),则y=∫g(x,C1)dx+C2y=\int g(x,C_1)dx+C_2y=∫g(x,C1)dx+C2
y′′=f(y,y′)y''=f(y,y')y′′=f(y,y′)情形(缺少x)
- 缺少x,令y′=py'=py′=p,y′′=dpdx=dpdy⋅dydx=dpdy⋅py''=\frac{dp}{dx}=\frac{dp}{dy}\cdot \frac{dy}{dx}=\frac{dp}{dy}\cdot py′′=dxdp=dydp⋅dxdy=dydp⋅p,这样就将原方程变为一阶方程pdpdy=f(y,p)p\frac{dp}{dy}=f(y,p)pdydp=f(y,p)
- 按照一阶方程求解并且还原
三、高阶常系数微分方程
1.能写成y′′+py′+qy=f(x)y''+py'+qy=f(x)y′′+py′+qy=f(x)形式的

2.能写成y′′+py′+qy=f1(x)+f2(x)y''+py'+qy=f_1(x)+f_2(x)y′′+py′+qy=f1(x)+f2(x)形式的

3.通解和特解的求解
通解:

上述是y′′+py′+qy=0y''+py'+qy=0y′′+py′+qy=0的通解,但是题目需要求解的是y′′+py′+qy=f(x)y''+py'+qy=f(x)y′′+py′+qy=f(x),因此还需要针对自由项f(x)求其特解
特解:

我们可以看到,对于y′′+py′+qy=f(x)y''+py'+qy=f(x)y′′+py′+qy=f(x)的通解一共有两个部分组成:一个是其次微分方程y′′+py′+qy=0y''+py'+qy=0y′′+py′+qy=0的通解,另外一个是针对自由项f(x)的特解。
另外,对于通解应该要有更深的理解:符合通解形式的任一特解,都是可以代入原方程的,是原方程的解。比如y′′+2y′+y=0y''+2y'+y=0y′′+2y′+y=0的通解是(C1+C2x)ex(C_1+C_2x)e^x(C1+C2x)ex,那么xex和ex都符合通解形式,都是y′′+2y′+y=0y''+2y'+y=0y′′+2y′+y=0的解
另外,我们也可以知道,对于y′′+py′+qy=f(x)y''+py'+qy=f(x)y′′+py′+qy=f(x)的特解y1y_1y1和y2y_2y2,则通过y1−y2y_1-y_2y1−y2可以求出
四、n阶导数微分方程
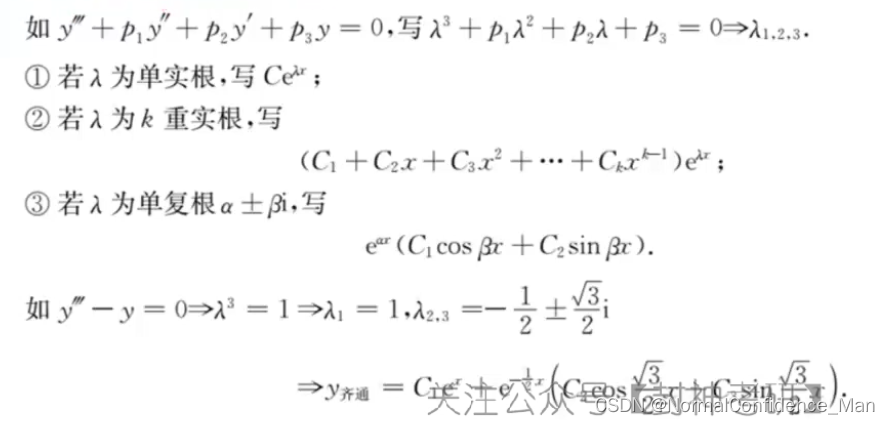
五、换元法求解微分方程
1.求导公式逆用换元
(siny)x′=cosydydx(sin y)'_x=cos y \frac{dy}{dx}(siny)x′=cosydxdy,令sin y=z,则dzdx=cosydydx\frac{dz}{dx}=cos y \frac{dy}{dx}dxdz=cosydxdy








 本文详细介绍了微分方程的基本概念和解法,包括一阶微分方程的分离变量法、齐次型、线性型,以及二阶可降阶和高阶常系数微分方程的处理。同时阐述了通解、特解的概念,以及如何通过换元法和特解求解特定类型的微分方程。
本文详细介绍了微分方程的基本概念和解法,包括一阶微分方程的分离变量法、齐次型、线性型,以及二阶可降阶和高阶常系数微分方程的处理。同时阐述了通解、特解的概念,以及如何通过换元法和特解求解特定类型的微分方程。
















 3282
3282

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








