高等数学——微分方程

最新推荐文章于 2024-10-09 08:58:20 发布

「已注销」

最新推荐文章于 2024-10-09 08:58:20 发布

阅读量3.2k

点赞数 1

文章标签：几何学抽象代数

本文链接：https://blog.youkuaiyun.com/m0_53412274/article/details/117192048

版权

这篇博客探讨了高等数学中的微分方程，重点是一阶线性微分方程和常系数非齐次线性微分方程的解法。介绍了通解公式，并提供了特解的设定方法，如f(x)=P(m)eλx型和eλx[Pm(x)cosωx+Pn(x)sinωx]型问题的处理策略。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

1.答题模板
2. 一阶线性微分方程
3.常系数非齐次线性微分方程
- $f(x)=P(m)e^{λx}型$
- $f(x)=e^{\lambda x}[P_m(x)cos{\omega}x+P_n(x)sin{\omega}x]型$

1.答题模板

微分方程。各位是不是学的很酸爽呢？其实本章内容逻辑非常简单，主要是微分方程的形式和种类太多，难以记忆。
【微分方程赋】

                         离齐线，二阶常

                         欧拉差分全伯降！

                         巧变形，化标准，

                         套路求解莫慌张！

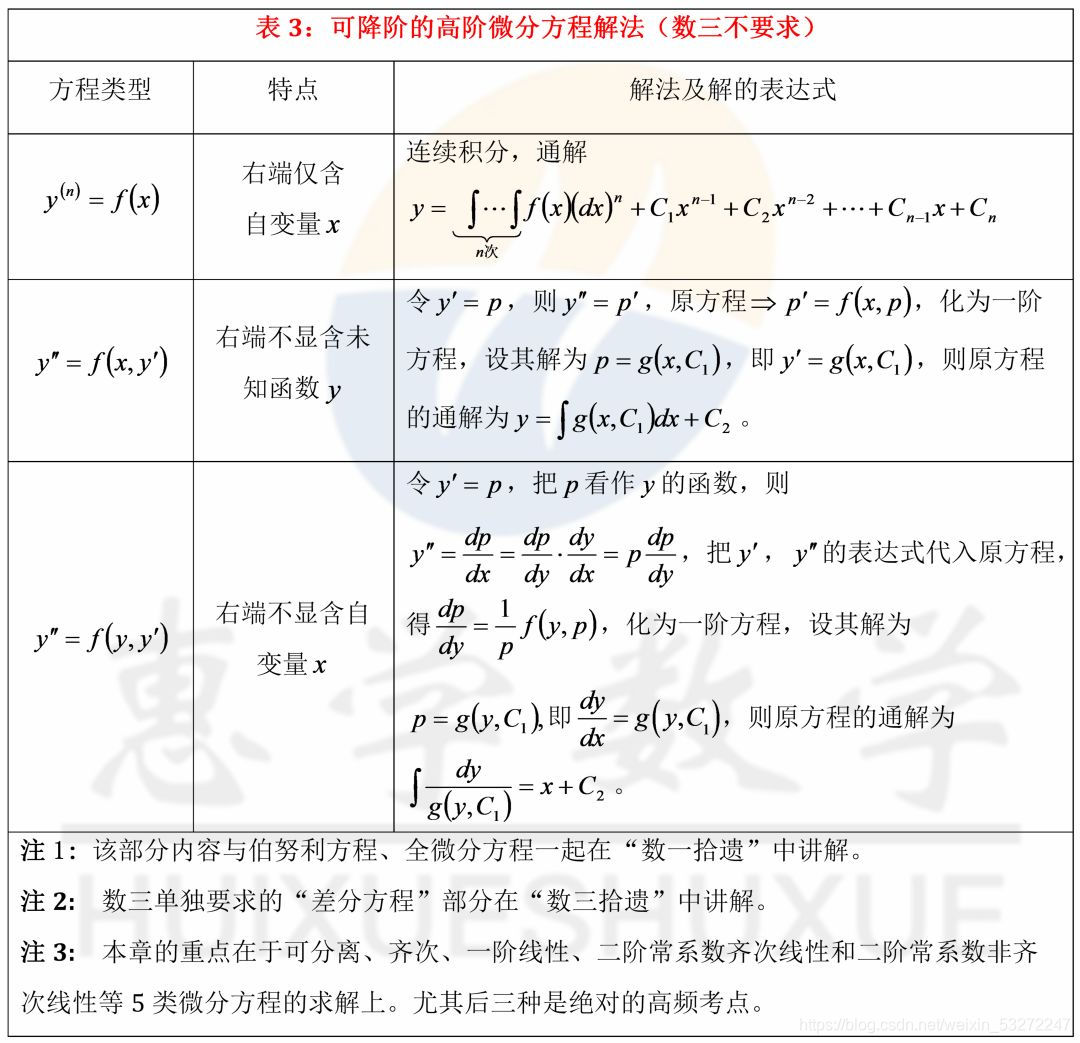
【释义】这首破诗的前两句是我们在本科范围内常见的微分方程的类型——可分离变量方程，齐次方程，一阶线性微分方程，二阶常系数线性方程，欧拉方程，差分方程，全微分方程，伯努利方程，可降阶方程，当然应付期末考试最主要是第一句的类型。这首破诗的后两句是说求解微分方程的步骤是固定的。首先要要通过巧变形（初等变形，变量互换，变量代换，叠加原理）把所给方程化成标准形式，然后按照固定步骤求解即可（参见表格1~表格3）。

    至于考试题型，无非就是已知方程求解，或者已知解求方程。至于大家头疼的应用问题，虽然具有很强的实际意义，但是考试中反而出现的不多。

在这里插入图片描述

2. 一阶线性微分方程

$y^{'}+P(x)y=Q(x)$
通解： $y=e^{-\int P(x)dx }[C+\int Q(x)e^{\int p(x)dx}dx]$
注意通解可以写以下形式：

最低0.47元/天解锁文章