离散数学——关系

序偶与笛卡儿积

两个具有固定次序的元素 a，b 组成一个有序对被称为$序偶$，记作 $<a，b>$，其中 a 称作第一个元素，b 称作第二个元素

任意给定两个集合 A 和 B ，所有第一元素属于 A，第二元素属于 B 的序偶所组成的集合，称为 A 和 B 的$笛卡尔积$，记作 $A\times B$
A × B ＝ { < x , y > ∣ x ∈ A , y ∈ B } A×B＝\{<x,y>|x∈A,y∈B\} A×B＝{<x,y>∣x∈A,y∈B}

性质:
$$\begin{gathered} Ø\times B＝A\times Ø＝Ø \\ A\times B\ne B\times A \\ (A\times B)\times C\ne A\times (B\times C) \\ A\times A\times ...\times A=A^n \\ 笛卡儿积运算对\cup ,\cap 或-运算满足分配律 \end{gathered}$$

关系的概念、性质及运算

关系的概念

R=A×A	全等关系
R=Ø	空关系
A=B R⊆A×B	二元关系
IA={<x,x>|x∈A}	恒等关系

$二元关系$：
$$\begin{gathered} 如果<x,y>\in R，则记作xRy \\ 如果<x,y>\notin R，则记作x\bar{R}y \\ R中所有序偶的第一个元素称为R的定义域，记作domR \\ R中所有序偶的第二个元素称为R的值域，记作ranR \end{gathered}$$

关系的表示

$关系矩阵$
$$m_{ij}=\{\begin{array}{ll}1,& 当<x_i,y_i>\in R;\\ 0,& 当<x_i,y_i>\notin R.\end{array}$$

关系的性质

xRx 对角线均为 1	自反关系
xRy → yRx 成对元素同时为 1	对称关系
xRy∧yRz → xRz	传递关系
x$\bar{R}$x 对角线均为 0	反自反关系
xRy∧yRx → x=y 成对元素不同时为 1	反对称关系

关系的复合运算

设 R 是从 X 到 Y 的关系，S 是从 Y 到 Z 的关系，则 R 和 S 的复合是一个从 X 到 Z 的二元关系，记作 $R◦S$，为 R 和 S 的$复合关系$

$$\begin{gathered} (F◦G)◦H=F◦(G◦H)结合律 \\ R◦R◦...◦R=R^n \\ 复合运算对\cup ,\cap 运算满足分配律 \end{gathered}$$

关系的逆运算

$逆关系$：
$$R^{-1}=<y,x>|<x,y>\in R$$

关系的闭包运算

自反闭包	$$r(R)=R\cup I_A$$
对称闭包	$$s(R)=R\cup R^{-1}$$
传递闭包	$$t(R)=R\cup R^2\cup ...=\bigcup _{i=1}^n{R}^i$$

$$\begin{gathered} rs(R)=sr(R) \\ rt(R)=tr(R) \\ st(R)\subseteq ts(R) \end{gathered}$$

特殊关系

等价关系

设 R 是集合 X 上的二元关系，若 R 是$自反的、对称的和传递的$，则称 R 是$等价关系$

A 可以$划分$成两两不相交的非空子集（$划分块$）的并集
交 叉 划 分 A ⊓ B = { A i ∩ B j ∣ A i ∩ B j ≠ Ø } \textcolor{red}{交叉划分 A\sqcap B}=\{A_i∩B_j|A_i∩B_j≠Ø\} 交叉划分A⊓B={Ai​∩Bj​∣Ai​∩Bj​​=Ø}

设 R 是集合 X 上的等价关系，$\forall x\in X$，则所有与 x 具有等价关系 R 的元素的集合称为元素 x 形成的$等价类$，记作 ${\left[x\right]}_R$，即 [ x ] R = { a ∣ a ∈ X ∧ x R a } \left [ x \right ]_{R}=\left \{ a|a\in X\wedge xRa \right \} [x]R​={a∣a∈X∧xRa}

集合 X 上所有元素形成的 R 等价类的集合称为 X 关于 R 的$商集$，用 $X/R$ 表示，即 X / R = { [ a ] R ∣ a ∈ X } X/R=\left \{ \left [ a \right ]_{R}|a\in X \right \} X/R={[a]R​∣a∈X}

• 例
  R 是 整 数 集 Z 上 的 模 4 同 余 关 系 ， 求 解 Z / R . Z / R = { [ 0 ] R , [ 1 ] R , [ 2 ] R , [ 3 ] R } R 是整数集 Z 上的模 4 同余关系，求解 Z/R. \\Z/R=\{[0]_R,[1]_R,[2]_R,[3]_R\} R是整数集Z上的模4同余关系，求解Z/R.Z/R={[0]R​,[1]R​,[2]R​,[3]R​}

相容关系

设 R 是定义在集合 X 上的二元关系，若 R 满足$自反的、对称的$性质，则称 R 是$相容关系$

设 R 是集合 X 上的相容关系，且 $C\subseteq X$，若对 C 中任意两个元素 $c_1$ 和 $c_2$ ，有$<c_1,c_2>\in R$，称 C 是由相容关系 R 产生的$相容类$
设 R 是集合 X 上的相容关系，不能真包含在其他相容类中的相容类，称作$极大相容类$
在关系简图中，若有子图 G，使子图中$任何两点都有连线$，则称 G 是$完全多边形$.不能找到别的完全多边形真包含该子图，则称此完全多边形是$极大完全多边形$.
极大完全多边形所对应的顶点集合就是极大相容类

$覆盖$：
$$\begin{gathered} {A}_i\subseteq A(i=1,2,...,m) \\ {A}_i\ne \varnothing \\ \bigcup _{i=1}^m{A}_i=A \end{gathered}$$
所有极大相容类构成的集合称为 X 的$完全覆盖$

偏序关系

设 R 是集合 X 上的二元关系，如果 R 是$自反的、反对称的和传递的$，则称 R 是 X 中的$偏序关系$，一般记作 $\le$.带有偏序关系的集合称为$偏序集$，记作$<X,\le >$

$设 \leqslant 是集合 X 上的偏序关系，a,b\in X，若 a\leq b 或 b\leq a，则称 a，b $可比较的$，否则称a，b是不可比较的.$

$哈塞图$

1. $省略所有节点的自回路$
2. $都是单向边，若x<y就把x画在y的下方，令所有边的方向都是向上的$
3. $若a\le b，b\le c，则有a\le c，故连接a与c的有向边省略$

	b 在集合内，a 不一定
极大元	$没有任何其他元素x满足b\le x$
极小元	$没有任何其他元素x满足x\le b$
最大元	$所有子集元素x满足x\le b$
最小元	$所有子集元素x满足b\le x$
上界	$所有子集元素x满足x\le a$
下界	$所有子集元素x满足a\le x$
上确界	$最小上界，记作lubB$
下确界	$最大下界，记作glbB$

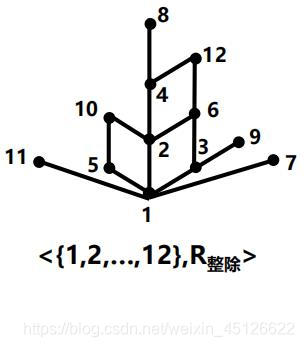	{1,3,4,5,6,12}	{1,2,3,6,12}	{3,5,6}
极大元	5,12	12	5,6
极小元	1	1	3,5
最大元		12
最小元	1	1
上界		12
下界	1	1	1
上确界		12
下确界	1	1	1

全序关系

	任一单元素子集既是链也是反链
全序关系	任何两个元素都是$可比较的$
全序集	$<A,\le >$
链	全序集
链的长度	元素的个数
反链	任何两个不同元素之间都$没有关系$
良序关系	任一非空子集都有$最小元$
拟序关系	反自反的、反对称的、传递的