【C++】【二叉树】【AVL 树】构建avl tree 类

最新推荐文章于 2024-10-15 15:30:22 发布
原创 最新推荐文章于 2024-10-15 15:30:22 发布 · 539 阅读 · 1 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#二叉树 #数据结构 #avl

本文深入讲解AVL树的原理及实现，包括恢复平衡的四种情况、插入与删除节点的方法，并提供完整的AVL树类实现代码。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

文章目录

前言

AVL树的引入是为了改造BST 的不平衡性，防止退化为链表。BST 类的构造在文末有链接。

AVL树使得其任一节点的左右子树高度差不超过1。平衡性相对宽松。使得其可以有看起来不平衡但却认为平衡的结构。

而二叉堆、线段树等平衡二叉树是叶子节点的高度差不超过1。

其在插入和删除的时候，都需要从插入、删除节点处向上维护平衡。

一、重点解析

1、恢复平衡

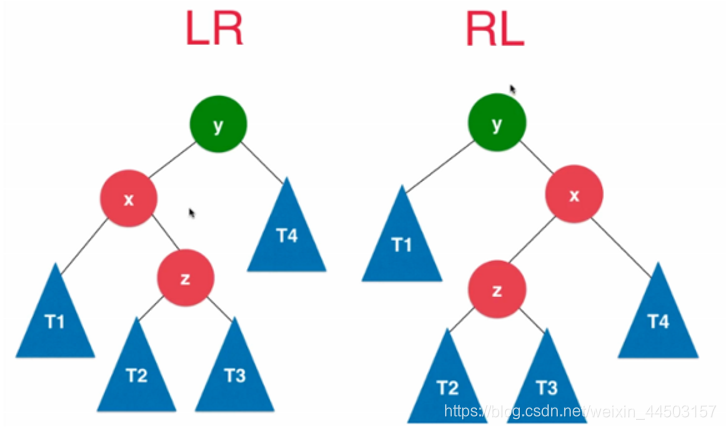
恢复平衡分为了四种情况，分别记为LL、RR、LR、RL；

LL:向左子树的左孩子插入节点导致不平衡；解决方案：右旋

RR:向右子树的右孩子插入节点导致不平衡；解决方案：左旋

LR:向左子树的右孩子插入节点导致不平衡；解决方案：左子树左旋+当前节点右旋

RL:向右子树的左孩子插入节点导致不平衡；解决方案：右子树右旋+当前节点左旋

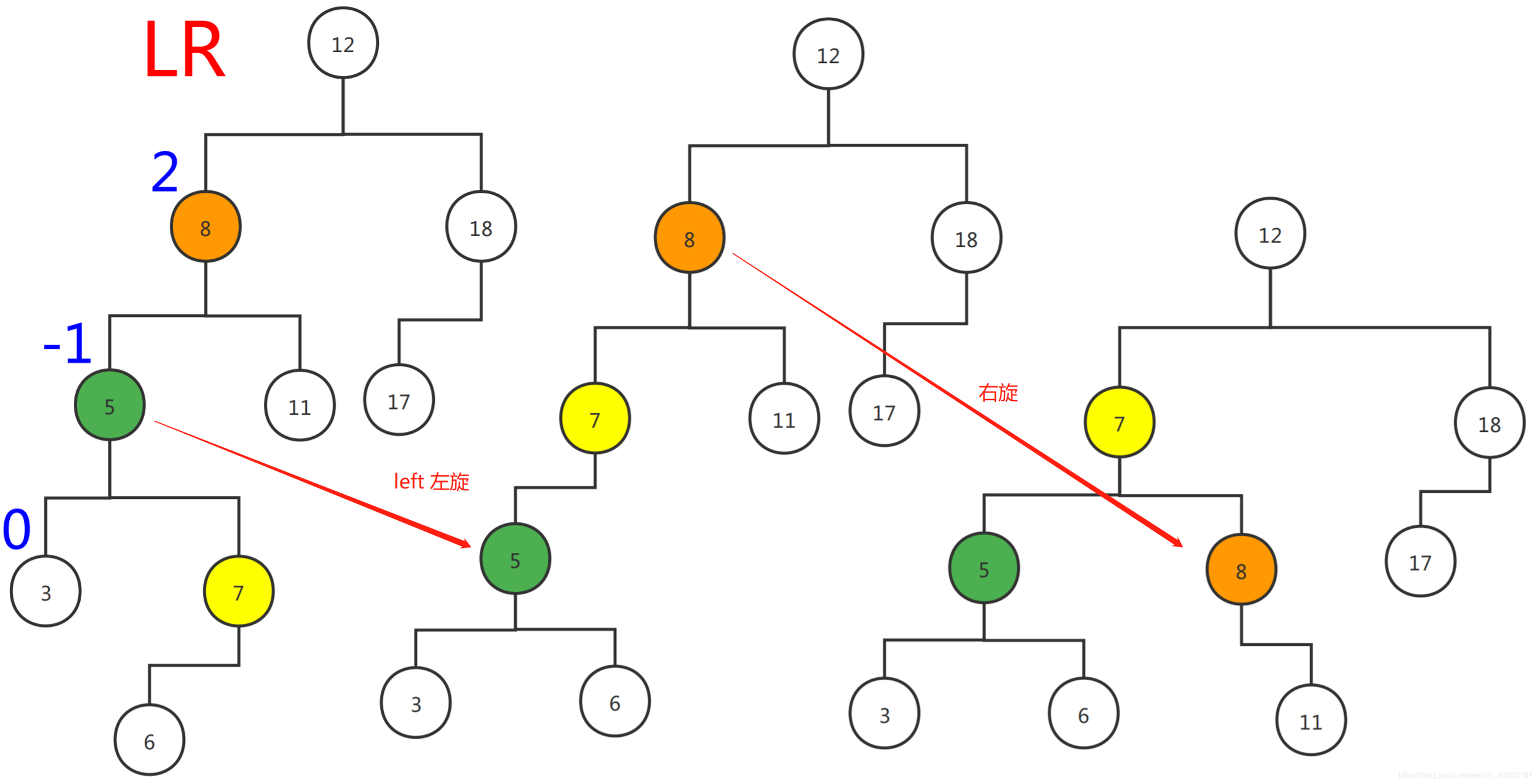
下面分别是LL、RR、LR、RL；最后一张图为LR 进行左旋+右旋后的结果
在这里插入图片描述
在这里插入图片描述

在这里插入图片描述

这里是向左子树的右孩子插入节点 6.使得其变成LR，然后对左子树节点5进行左旋，然后再整体右旋。

在这里插入图片描述

2、插入节点

相对于BST，插入节点加入了：

  1. 对当前节点的高度计算；
  2. 对平衡因子的计算（左右子树的高度计算）；
  3. 根据平衡性，分四种情况进行左旋右旋->以恢复平衡。
// 向以node为根的二叉搜索树中,插入节点(key, value)
// 返回插入新节点后的二叉搜索树的根
Node *add(Node *node, Key key, Value value) {
    if (node == nullptr) {
        size++;
        return new Node(key, value);
    }
    if (key == node->key) {
        node->value = value;
    } else if (key < node->key) {
        node->left = add(node->left, key, value);
    } else {
        node->right = add(node->right, key, value);
    }
    node->height = 1 + std::max(getHeight(node->left), getHeight(node->right));
    int balanceFactor = getBalanceFactor(node);

    if (balanceFactor > 1 && getBalanceFactor(node->left) >= 0) {
        return rightRotate(node);
    }

    if (balanceFactor < -1 && getBalanceFactor(node->right) <= 0) {
        return leftRotate(node);
    }

    if (balanceFactor > 1 && getBalanceFactor(node->left) < 0) {
        node->left = leftRotate(node->left);
        return rightRotate(node);
    }

    if (balanceFactor < -1 && getBalanceFactor(node->right) > 0) {
        node->right = rightRotate(node->right);
        return leftRotate(node);
    }

    return node;
}

3、删除节点

相对于BST，删除节点加入了：

  1. 删除节点后，将要返回的根节点暂存。
  2. 对当前节点的高度计算；
  3. 对平衡因子的计算（左右子树的高度计算）；
  4. 根据平衡性，分四种情况进行左旋右旋->以恢复平衡。

取消了删除最值，因为还要给删除最值中添加恢复平衡的代码，不如就只复用remove 的代码即可。

// 删除掉以node为根的二分搜索树中键值为key的节点
// 返回删除节点后新的二分搜索树的根
Node *remove(Node *node, Key key) {
    if (node == nullptr) {
        return nullptr;
    }

    Node *retNode;
    if (key < node->key) {
        node->left = remove(node->left, key);
        retNode = node;
    } else if (key > node->key) {
        node->right = remove(node->right, key);
        retNode = node;
    } else {
        if (node->left == nullptr) {
            Node *rightNode = node->right;
            delete node;
            size--;
            retNode = rightNode;
        } else if (node->right == nullptr) {
            Node *leftNode = node->left;
            delete node;
            size--;
            retNode = leftNode;
        } else {
            Node *successor = new Node(minimum(node->right));
            size++;

            successor->right = remove(node->right, successor->key);
            successor->left = node->left;

            delete node;
            size--;

            retNode = successor;
        }
    }
    if (retNode == nullptr) 
    	return nullptr;

    retNode->height = 1 + std::max(getHeight(retNode->left), getHeight(retNode->right));
    int balanceFactor = getBalanceFactor(retNode);

    if (balanceFactor > 1 && getBalanceFactor(retNode->left) >= 0) {
        return rightRotate(retNode);
    }

    if (balanceFactor < -1 && getBalanceFactor(retNode->right) <= 0) {
        return leftRotate(retNode);
    }

    if (balanceFactor > 1 && getBalanceFactor(retNode->left) < 0) {
        retNode->left = leftRotate(retNode->left);
        return rightRotate(retNode);
    }

    if (balanceFactor < -1 && getBalanceFactor(retNode->right) > 0) {
        retNode->right = rightRotate(retNode->right);
        return leftRotate(retNode);
    }

    return retNode;
}

3、析构函数

析构函数，需要用到后序遍历的思想。

即，删除当前节点，得先将其左右子树都删除掉，否则无法删除整个树。

下面代码，其实就是后序遍历的递归形式的析构函数。

    // 析构函数, 释放二分搜索树的所有空间
    ~BST(){
        destroy( root );
    }

    // 释放以node为根的二分搜索树的所有节点
    // 采用后续遍历的递归算法
    void destroy(Node* node){

        if( node != NULL ){
            destroy( node->left );
            destroy( node->right );

            delete node;
            count --;
        }
    }

二、完整AVL tree类

完整代码取自bobo老师及相关同学的github，文末有路径。

template<typename Key, typename Value>
class AVLTree {
private:
    struct Node {
        Key key;
        Value value;
        Node *left;
        Node *right;
        int height;

        Node(Key key, Value value) {
            this->key = key;
            this->value = value;
            this->left = this->right = nullptr;
            height = 1;
        }

        Node(Node *node) {
            this->key = node->key;
            this->value = node->value;
            this->left = node->left;
            this->right = node->right;
            this->height = node->height;
        }
    };

    Node *root;
    int size;

public:

    AVLTree() {
        root = nullptr;
        size = 0;
    }

    ~AVLTree() {
        destroy(root);
    }

    int getSize() {
        return size;
    }

    int isEmpty() {
        return size == 0;
    }

    int getHeight(Node *node) {
        if (node == nullptr) {
            return 0;
        }
        return node->height;
    }

    int getBalanceFactor(Node *node) {
        if (node == nullptr) {
            return 0;
        }
        return getHeight(node->left) - getHeight(node->right);
    }

    bool isBST() {
        std::vector<Key> keys;
        inOrder(root, keys);
        for (int i = 1; i < keys.size(); ++i) {
            if (keys.at(i - 1) < keys.at(i)) {
                return false;
            }
        }
        return true;
    }

    bool isBalanced() {
        return isBalanced(root);
    }

    void add(Key key, Value value) {
        root = add(root, key, value);
    }

    bool contains(Key key) {
        return getNode(root, key) != nullptr;
    }

    Value *get(Key key) {
        Node *node = getNode(root, key);
        return node == nullptr ? nullptr : &(node->value);
    }

    void set(Key key, Value newValue) {
        Node *node = getNode(root, key);
        if (node != nullptr) {
            node->value = newValue;
        }
    }

    // 从二叉树中删除键值为key的节点
    Value *remove(Key key) {
        Node *node = getNode(root, key);
        if (node != nullptr) {
            root = remove(root, key);
            return &(node->value);
        }
        return nullptr;
    }

private:

    // 向以node为根的二叉搜索树中,插入节点(key, value)
    // 返回插入新节点后的二叉搜索树的根
    Node *add(Node *node, Key key, Value value) {
        if (node == nullptr) {
            size++;
            return new Node(key, value);
        }
        if (key == node->key) {
            node->value = value;
        } else if (key < node->key) {
            node->left = add(node->left, key, value);
        } else {
            node->right = add(node->right, key, value);
        }
        node->height = 1 + std::max(getHeight(node->left), getHeight(node->right));
        int balanceFactor = getBalanceFactor(node);

        if (balanceFactor > 1 && getBalanceFactor(node->left) >= 0) {
            return rightRotate(node);
        }

        if (balanceFactor < -1 && getBalanceFactor(node->right) <= 0) {
            return leftRotate(node);
        }

        if (balanceFactor > 1 && getBalanceFactor(node->left) < 0) {
            node->left = leftRotate(node->left);
            return rightRotate(node);
        }

        if (balanceFactor < -1 && getBalanceFactor(node->right) > 0) {
            node->right = rightRotate(node->right);
            return leftRotate(node);
        }

        return node;
    }

    // 在以node为根的二叉搜索树中查找key所对应的Node
    Node *getNode(Node *node, Key key) {
        if (node == nullptr) {
            return nullptr;
        }
        if (key == node->key) {
            return node;
        } else if (key < node->key) {
            return getNode(node->left, key);
        } else {
            return getNode(node->right, key);
        }
    }

    void destroy(Node *node) {
        if (node != nullptr) {
            destroy(node->left);
            destroy(node->right);
            delete node;
            size--;
        }
    }

    // 在以node为根的二叉搜索树中,返回最小键值的节点
    Node *minimum(Node *node) {
        if (node->left == nullptr)
            return node;
        return minimum(node->left);
    }

    // 在以node为根的二叉搜索树中,返回最大键值的节点
    Node *maximum(Node *node) {
        if (node->right == nullptr)
            return node;
        return maximum(node->right);
    }

    // 删除掉以node为根的二分搜索树中的最小节点
    // 返回删除节点后新的二分搜索树的根
    Node *removeMin(Node *node) {
        if (node->left == nullptr) {
            Node *rightNode = node->right;
            delete node;
            size--;
            return rightNode;
        }

        node->left = removeMin(node->left);
        return node;
    }

    // 删除掉以node为根的二分搜索树中的最大节点
    // 返回删除节点后新的二分搜索树的根
    Node *removeMax(Node *node) {
        if (node->right == nullptr) {
            Node *leftNode = node->left;
            delete node;
            size--;
            return leftNode;
        }

        node->right = removeMax(node->right);
        return node;
    }

    // 删除掉以node为根的二分搜索树中键值为key的节点
    // 返回删除节点后新的二分搜索树的根
    Node *remove(Node *node, Key key) {
        if (node == nullptr) {
            return nullptr;
        }

        Node *retNode;
        if (key < node->key) {
            node->left = remove(node->left, key);
            retNode = node;
        } else if (key > node->key) {
            node->right = remove(node->right, key);
            retNode = node;
        } else {
            if (node->left == nullptr) {
                Node *rightNode = node->right;
                delete node;
                size--;
                retNode = rightNode;
            } else if (node->right == nullptr) {
                Node *leftNode = node->left;
                delete node;
                size--;
                retNode = leftNode;
            } else {
                Node *successor = new Node(minimum(node->right));
                size++;

                successor->right = remove(node->right, successor->key);
                successor->left = node->left;

                delete node;
                size--;

                retNode = successor;
            }
        }
        if (retNode == nullptr) {
            return nullptr;
        }
        retNode->height = 1 + std::max(getHeight(retNode->left), getHeight(retNode->right));
        int balanceFactor = getBalanceFactor(retNode);

        if (balanceFactor > 1 && getBalanceFactor(retNode->left) >= 0) {
            return rightRotate(retNode);
        }

        if (balanceFactor < -1 && getBalanceFactor(retNode->right) <= 0) {
            return leftRotate(retNode);
        }

        if (balanceFactor > 1 && getBalanceFactor(retNode->left) < 0) {
            retNode->left = leftRotate(retNode->left);
            return rightRotate(retNode);
        }

        if (balanceFactor < -1 && getBalanceFactor(retNode->right) > 0) {
            retNode->right = rightRotate(retNode->right);
            return leftRotate(retNode);
        }

        return retNode;
    }

    void inOrder(Node *node, std::vector<Key> keys) {
        if (node == nullptr) {
            return;
        }
        inOrder(node->left, keys);
        keys.push_back(node->key);
        inOrder(node->right, keys);
    }

    bool isBalanced(Node *node) {
        if (node == nullptr) {
            return true;
        }

        int balanceFactor = getBalanceFactor(node);
        if (std::abs(balanceFactor) > 1) {
            return false;
        }

        return isBalanced(node->left) && isBalanced(node->right);
    }

    Node *leftRotate(Node *y) {
        Node *x = y->right;
        Node *tmp = x->left;
        x->left = y;
        y->right = tmp;
        y->height = std::max(getHeight(y->left), getHeight(y->right)) + 1;
        x->height = std::max(getHeight(x->left), getHeight(x->right)) + 1;
        return x;
    }

    Node *rightRotate(Node *y) {
        Node *x = y->left;
        Node *tmp = x->right;
        x->right = y;
        y->left = tmp;
        y->height = std::max(getHeight(y->left), getHeight(y->right)) + 1;
        x->height = std::max(getHeight(x->left), getHeight(x->right)) + 1;
        return x;
    }
};

参考

模板类、模板函数设计

二叉搜索树类 实现

bobo老师github

houpengfei的github

C++进阶——AVL树的构建
weixin_43635473的博客
05-15 718
AVLTreeNode(const pair < k , v > & kv) //节点构造函数 : _left(nullptr) , _right(nullptr) , _parent(nullptr) , _kv(kv) , _be(0) {int _be;
模拟实现AVLTree超详解（C++）
m0_67430750的博客
05-09 1033
模拟实现AVLTree万字详解，包括了KV模型和K模型。同时封装了正反迭代器（const和非const）。
构造avl树_图解AVL树
weixin_39641450的博客
12-15 2532
1：AVL树简介二叉搜索树在一般情况下其搜索的时间复杂度为O(logn)，但某些特殊情况下会退化为链表，导致树的高度变大且搜索的时间复杂度变为O(n)，发挥不出树这种数据结构的优势，因此平衡二叉树便应运而生，通过保证树的高度来保证查询的时间复杂度为O(logn)，想想人类实在是太聪明了！2：构造AVL树在构造一棵AVL树的时候如何保持平衡呢？其手段便是通过各种旋转变换来调整以此保证整棵树的高度，调...
AVL树的模板类实现
Moyu的专栏
06-13 876
一、介绍        在计算机科学中，AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下的时间复杂度都是O(logn)。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis，他们在1962年的论文《An ...
平衡二叉树(AVLTree)的构造等——超详细
qq_44819750的博客
07-28 2645
平衡二叉树概念 二叉搜索树虽可以缩短查找的效率，但如果数据有序或接近有序二叉搜索树将退化为单支树，查找元素相当 于在顺序表中搜索元素，效率低下。因此，两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年 发明了一种解决上述问题的方法：当向二叉搜索树中插入新结点后，如果能保证每个结点的左右子树高度之 差的绝对值不超过1(需要对树中的结点进行调整)，即可降低树的高度，从而减少平均搜索长度。 一棵AVL树或者是空树，或者是具有以下性质的二叉搜索树： 1.它的左右子树都是AVL
c++——AVL树
Britney_dark的博客
11-08 1885
如果结果不如你所愿，就在尘埃落定前奋力一搏！
『 C++ 』AVL树详解 ( 万字 )
小侯宝的博客
01-15 982
从上文可知,AVL树可以看作是一棵搜索二叉树,其为基于搜索二叉树在此基础上对树做了平衡的操作使其在结构上变得平衡不至于在极端情况下出现"歪脖子树"的情况;AVL树的定义与平衡搜索二叉树的结构上呈现类似;//将节点进行typedefpublic:protected:private://节点指针该篇文章中重点实现AVL树中的插入操作;
avl.rar_avl_avl tree_binary search tree_tree_二叉树
09-21
AVL树是计算机科学中一种重要的自平衡二叉搜索树（binary search tree，BST），由G. M. Adelson-Velsky和E. M. Landis于1962年提出，因此得名AVL树。AVL树的主要特点是任何节点的两个子树的高度最大差别不超过1，这...
【C++】AVL树详解
muyuteacher的博客
02-29 1389
AVL树是一种高效的自平衡二叉搜索树，在计算机科学领域得到广泛应用。本文主要介绍了AVL树的概念、节点定义、AVL树的实现以及验证，其中包括对平衡因子的解释，研究在插入节点时，如何通过旋转来调节平衡因子来保持AVL树的特性。
【C++】详解STL之 AVL tree --- “额外平衡条件的”二叉搜索树
最新发布
2401_83431652的博客
10-15 1157
VL树是一种高度平衡的二叉搜索树，通过严格控制左右子树高度差（不超过1）来保证操作效率为O(logN)。文章详细介绍了AVL树的核心概念、平衡因子机制及实现方法，重点阐述了插入操作时的四种旋转调整策略（左/右单旋、左右/右左双旋）及其代码实现。通过平衡检测函数验证树的平衡性，并提供了测试案例展示其性能优势。AVL树在保证搜索效率的同时，有效解决了普通二叉搜索树可能退化为链表的问题。
AVL Tree(C++代码实现)
玩遍每座城
04-07 598
代码 #include <bits/stdc++.h> using namespace std; struct Node { int val; Node *left, *right; Node(int v):val(v),left(nullptr),right(nullptr){} }; struct AVLTree { Node *root; ...
c++实现AVL_tree
A_Bo的博客
10-23 828
写在前面 AVL_Tree是一棵自平衡的二叉树，在树中任意节点的左右子树之间的高度差小于等于1，很好的弥补了二叉搜索树有可能出现不平衡的情况，只是在二叉搜索树的基础上添加了四种旋转操作，使二叉搜索树变成自平衡的二叉搜索树 AVLTree的数据结构 首先它是一个二叉树，那么他一定包含左右子节点的信息，并且为了方便进行高度的判断调整等，还要包含高度信息，最后还要有当前节点的数值信息，所以他的数据...
AvlTree的C++实现
小昊
06-03 318
#ifndef AVL_TREE_H #define AVL_TREE_H #include "dsexceptions.h" #include <algorithm> #include <iostream> using namespace std; // AvlTree class // // CONSTRUCTION: zero parameter // // ******************PUBLIC OPERATIONS*********************
AVLTree的C++实现
lc331257229的专栏
05-27 1034
删除操作有个bug,
C++(数据结构与算法):50---平衡搜索树之AVL树（AVL Tree）
董哥的黑板报
02-07 1191
一、AVL树概述 如果搜索树的高度总是O(logn)，就能保证查找、插入、删除的时间为O(logn)。最坏情况下的高度为O(logn)的树称为平衡树 比较流行的一种平衡树是AVL树，它是Adelson-Velskii和Landis在1962年提出的 AVL树的定义 一棵空的树是AVL树 如果T是一棵非空的二叉树，T(L)和T(R)分别是其左子树和右子树，那么当T满足以下条件时，T是一棵A...
使用C++实现一个AVL树（泛型AVL类）
Chuancey的博客
04-26 216
实现AVL树的构建、插入结点、删除结点、AVL树的销毁等操作，已通过100条样例测试。第n个字符串有三种类型：PRE、IN、POST，分别代表最后AVL树以什么顺序输出。输出按照输入说明的输出格式打印AVL树，如果AVL树是空，打印EMPTY。
AVLTree的C++的实现
qq_46655061的博客
02-18 758
AVL树的添加元素实现，主要的旋转讲解。
AVL二叉树的实现（C++）
nanfang0的博客
12-10 832
使用C++实现AVL二叉树的插入，查找，删除，遍历等操作
【C++】AVL树
柯礼的博客
03-05 649
AVL树的学习
C++模板实现AVL树原理与应用
对于每个概念的深入理解和实现，AVL树的C++实现将涉及到具体的数据结构定义，包括节点结构、树的构造与销毁、元素的插入与删除、树的平衡操作等。实现时还需要注意各种边界条件和特殊情况的处理，确保树在各种操作...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值