模拟实现AVLTree超详解（C++）

😇 😇大家好，我是bug！今天来跟大伙谈谈AVLTree：
（代码可能会有一点问题，请各位老铁指正 😘 😘 ）

一、AVLTree的概念

🌵🌵 AVLTree：也叫做高度平衡二叉搜索树。通过对高度的控制来保证效率，而对于高度我们采用了旋转的方式来进行约束。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。相较于二叉搜索树，平衡二叉搜索树很好地避免了极端情况（插入的数据接近于有序），查找的时间复杂度为O（logN）。

🌵🌵K模型和KV模型 ：
K模型中只有key作为关键字，只存储key一个值。
而KV模型中存储了KV的键对值，即每个key值都有一个value与之对应。与K模型不一样的是多了个value与之绑定，其他部分没什么区别。

🍉 🍉同时相较于普通的二叉搜索树，我们在AVLTree中采用了三叉链和平衡因子，三叉链可以在某些方面带来便利，平衡因子用来控制树的平衡。 （当然，AVLTree的实现也可以不借助三叉链和平衡因子，有兴趣的小伙伴们可以去研究研究。）

🌵🌵 三叉链结构：每个结点有三个指针域，除了指向左孩子和右孩子还会指向父亲，如果是根结点，则父亲结点为nullptr。

🌵🌵平衡因子：即右子树的高度减去左子树的高度所得结果。(abs(平衡因子) <= 1)

二、AVLTree的插入

☀️ ☀️在开始插入操作前，我们先讲讲AVLTree的旋转操作。
AVLTree中的旋转操作包括左单旋，右单旋，左右双旋和右左双旋，共四种。 （下面我们直接在分类中按图说话，嘿嘿）

AVL树的插入过程比较复杂，一共有四种情况，要严格遵守其规则（下面例子为最简单的具象图）：

🌱 🌱 （1）“直线形状”

🌳🌳一、（右单旋）

🔍 🔍 当我们插入结点后出现下图情况时 :

（插入前p的平衡因子为0，g的平衡因子为-1；插入后p的平衡因子为-1，g的平衡因子为-2） 🔎 🔎 ：

🔑 此时，g的平衡因子变成了-2，违反了规则，所以我们要进行旋转操作。以g为旋转点，进行右单旋。

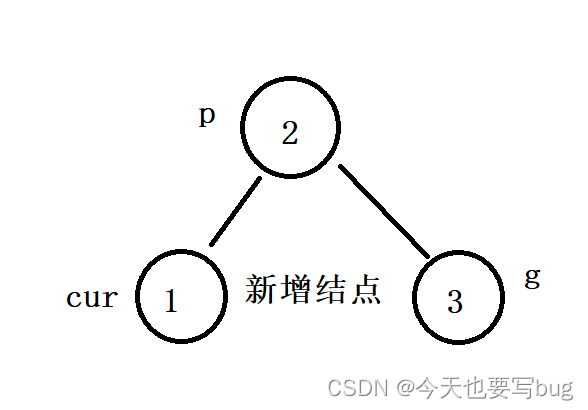
🔑 此时cur，p和g的平衡因子都变成了0，调整完成。

---

🌳🌳二、（左单旋）

🔍 🔍 和上面的情况刚好相反。当我们插入结点后出现下图情况时:

（插入前p的平衡因子为0，g的平衡因子为1；插入后p的平衡因子为1，g的平衡因子为2 ） 🔎 🔎 ：

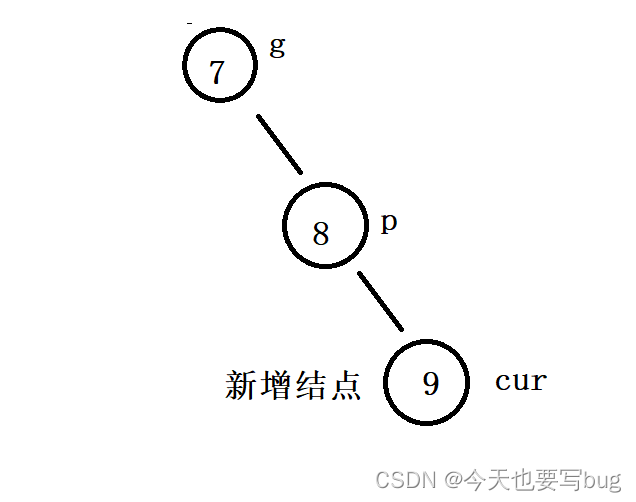
🔑 这时，我们要以g为旋转点进行左单旋，同时更新平衡因子。

🔑 三个结点的平衡因子都变成了0，调整完毕。

---

下面我们从中抽出AVLTree的抽象图模型：
📣 📣 1、右单旋：

🔑 此时以80为旋转点，进行右单旋，同时把80的右子树与_root进行链接。

---

📣 📣 2、左单旋

🔑 和右单旋情况类似，此时以80作为旋转点进行左单旋，同时把80的左子树和_root进行链接。

---

🌱 🌱（2）”折线形状“

🌳🌳一、（右左双旋）

🔍 🔍 当我们插入结点后变成下面这种情况 🔎 🔎 ：

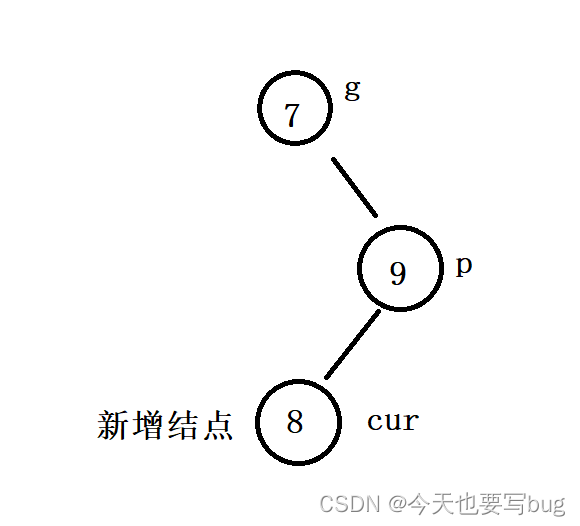
🔑 我们就要进行右左双旋了，要先以p为旋转点进行右单旋。（变成左单旋的情况）

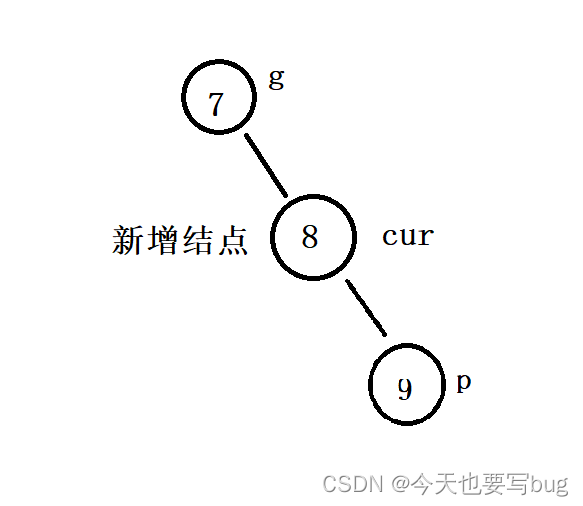
🔑 再以cur为旋转点进行左单旋。

---

🌳🌳 二、（左右双旋）

🔍 🔍 和上面的情况相反 🔎 🔎 ：

🔑 先以p为旋转点，进行左单旋。（旋转后和右单旋的情况一致）

🔑 再以cur为旋转点，进行右单旋 。

---

下面我们来抽出它的抽象图：
📣 📣 1、右左双旋

🔑 先以80为旋转点，进行右单旋，同时更新80和70的平衡因子。

🔑 再以50为旋转点，进行左单旋，同时更新50和70的平衡因子。

---

📣 📣 2、左右双旋

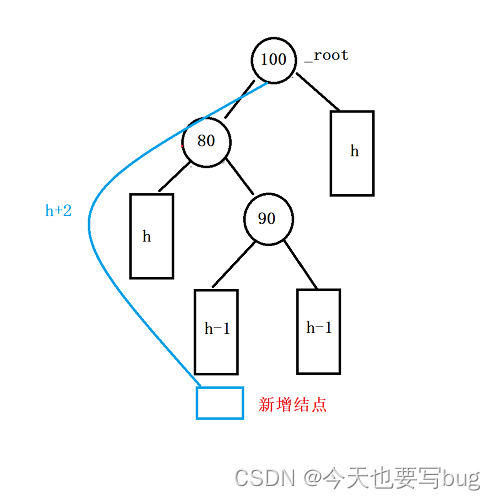
🔑 先以80为旋转点，进行左单旋，同时更新80和90的平衡因子。

🔑 再以90为旋转点，进行右单旋，同时更新100和90的平衡因子。

---

插入部分的内容比较复杂，希望大家能够多看看。 😜 😜

---

三、AVLTree的迭代器

💡 💡 简介：对于AVLTree（包括红黑树），我们引入了三叉链进行实现，这样有助于我们实现迭代器。
AVLTree的迭代器与list的迭代器类似，其都不是原生指针，而是进行封装之后的复杂结构。
这里我们会实现AVLTree的正向迭代器和反向迭代器。其中反向迭代器的内部封装了正向迭代器。

🌻 🌻 那我们是怎么实现AVLTree的正向迭代器呢？
（难点：自增自减的重载）

对于自增自减，我们按照中序完成。（以自增为例，自减和自增类似）
🔑 与_pnode中的数据最接近的一定是右子树的最左结点（按照中序）。

🔑 当_pnode的右子树存在，那么我们去找它右子树的最左结点。

🌴 🌴 当_pnode的右子树不存在，那我们只能向上去找，找到当前结点是父亲的左孩子的结点，这个时候的父亲结点就是我们的下个结点。（按照中序）

🌴 🌴 对于反向迭代器，其内部封装了正向迭代器，正向迭代器内要实现自减的重载，自减重载是反向迭代器的关键。

---

四、AVLTree的模拟实现

🍒 🍒这里模拟实现AVLTree树⬇️ ⬇️：

#pragma once

#include<iostream>
#include<assert.h>
#include<string>

using std::cin;
using std::cout;
using std::endl;
using std::pair;

namespace lz
{
   
	template<class K, class V>
	struct PairKeyOfValue
	{
   
		const K& operator()(const pair<const K, V>& kv){
    return kv.first; }
	};

	template<class K>
	struct KKeyOfValue
	{
   
		const K& operator()(const K& key)const {
    return key; }
	};

	template<class T>
	struct AVLTreeNode
	{
   
	public:
		AVLTreeNode<T>* _left;
		AVLTreeNode<T>* _right;
		AVLTreeNode<T>* _parent;

		//平衡因子
		//平衡因子等于右子树的高度减去左子树的高度
		int _bf;

		T _data;

		//构造函数
		AVLTreeNode(const T& data = T())
			:_left(nullptr)
			, _right(nullptr)
			, _parent(nullptr)
			, _bf(0)
			, _data(data)
		{
   }
	};

	template<class T,class Ref,class Ptr>
	struct iterator
	{
   
		typedef AVLTreeNode<T>* pNode;
		typedef Ref reference;
		typedef Ptr pointer;
		typedef const Ref const_reference;
		typedef const Ptr const_pointer;
		typedef iterator<T, Ref, Ptr> self;

	public:
		iterator(pNode pnode = nullptr)
			:_pnode(pnode)
		{
   }

		reference operator*() {
    return _pnode->_data; }
		const_reference operator*()const {
    return _pnode->_data; }
		pointer operator->() {
    return &operator*(); }
		const_pointer operator->()const {
    return &operator*(); }

		void increasement()
		{
   
			if (_pnode == nullptr)
				return ;

			//去找右子树的最左结点
			if (_pnode->_right != nullptr)
			{
   
				pNode left = _pnode->_right;
				while (left->_left)
					left = left->_left;

				_pnode = left;
				return ;
			}

			//右子树为空，我们向上找
			pNode parent = _pnode->_parent;
			pNode cur = _pnode;
			while (parent)
			{
   
				if (parent->_right == cur)
				{
   
					cur = parent;
					parent = parent->_parent;
				}
				else
					break;
			}

			_pnode = parent;
		}
		self& operator++() {
    increasement(); return *this; }
		self operator++(int) {
    pNode tmp = _pnode; increasement(); return self(tmp); }

		void decreasement()
		{
   
			if (_pnode == nullptr)
				return ;

			//左子树不为空时
			if (_pnode->_left != nullptr)
			{
   
				pNode right = _pnode->_left;
				while (right->_right)
					right = right->_right;

				_pnode = right;
				return;
			}

			//左子树为空
			pNode parent = _pnode->_parent;
			pNode cur = _pnode;
			while (parent)
			{
   
				if (parent->_left == cur)
				{
   
					cur = parent;
					parent = parent->_parent;
				}
				else
					break;
			}

			_pnode = parent;