1. 二维线性变换
对向量 [xy]\begin{bmatrix} x \\ y \end{bmatrix}[xy] 进行线性变换
[a11a12a21a22][xy]=[a11x+a12ya21x+a22y]=[x′y′] \begin{bmatrix} a_{11} &a_{12} \\ a_{21} &a_{22} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} a_{11}x + a_{12}y \\ a_{21}x + a_{22}y \end{bmatrix} = \begin{bmatrix} x' \\ y' \end{bmatrix} [a11a21a12a22][xy]=[a11x+a12ya21x+a22y]=[x′y′]
1.1 缩放(Scaling)
缩放变换是一种沿着 坐标轴作用 的变换
scale(sx,sy)=[sx00sy] scale(s_x,s_y) = \begin{bmatrix} s_x & 0 \\ 0 & s_y \end{bmatrix} scale(sx,sy)=[sx00sy]
除了 [00]\begin{bmatrix} 0 \\ 0 \end{bmatrix}[00] 保持不变,其他所有点变为 [sxxsyy]\begin{bmatrix} s_x x \\ s_y y \end{bmatrix}[sxxsyy]
第一种情况:x 方向和 y 方向均缩小0.5倍
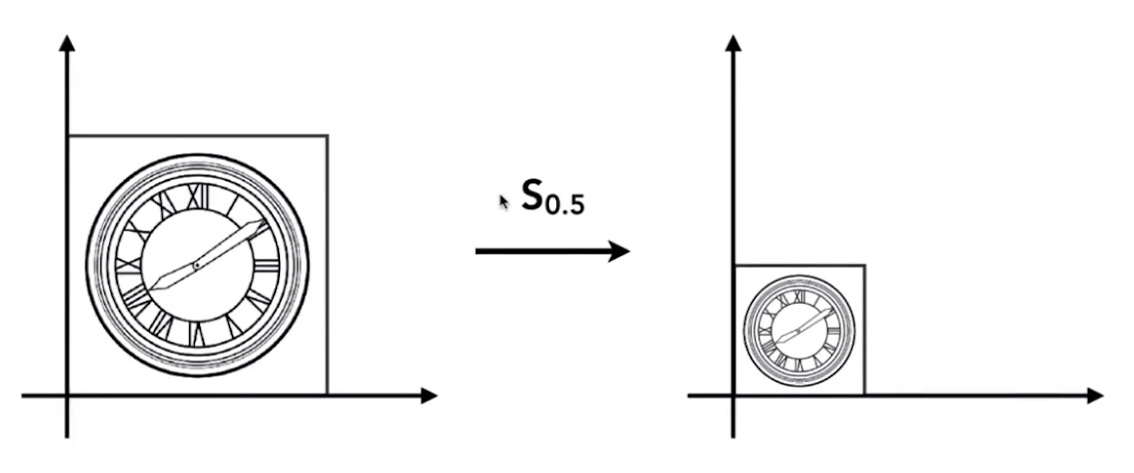
[x′y′]=[0.5000.5][xy] \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 0.5 & 0 \\ 0 & 0.5 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} [x′y′]=[0.5000.5][xy]
第二种情况:x 方向缩小 0.5 倍, y 方向不变
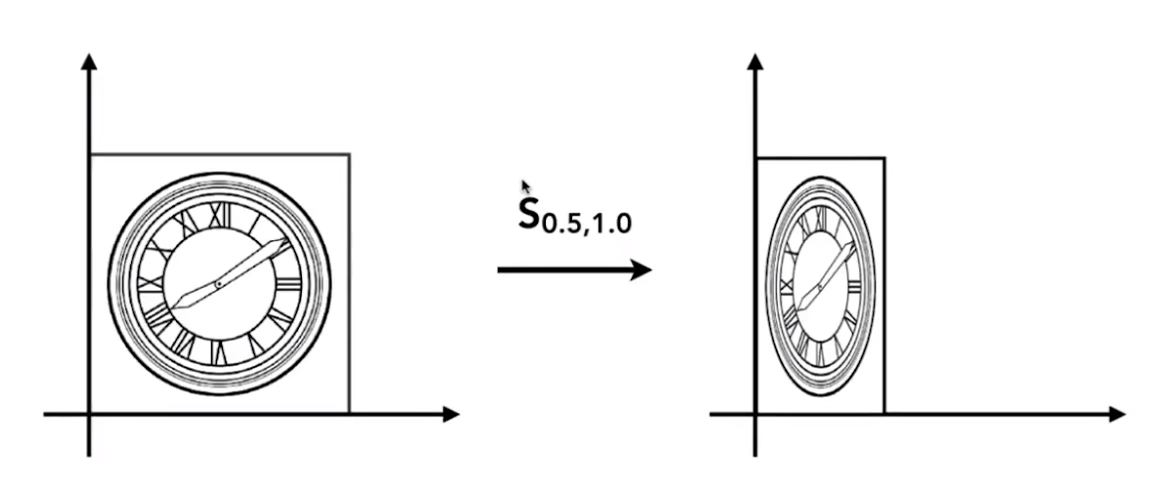
[x′y′]=[0.5001][xy] \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 0.5 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} [x′y′]=[0.5001][xy]
1.2 反射(Reflection)
进行一个镜像的变换
x′=−xy′=y \begin{aligned} &x' = -x \\ &y' = y \end{aligned} x′=−xy′=y
沿着 y 轴进行翻转操作
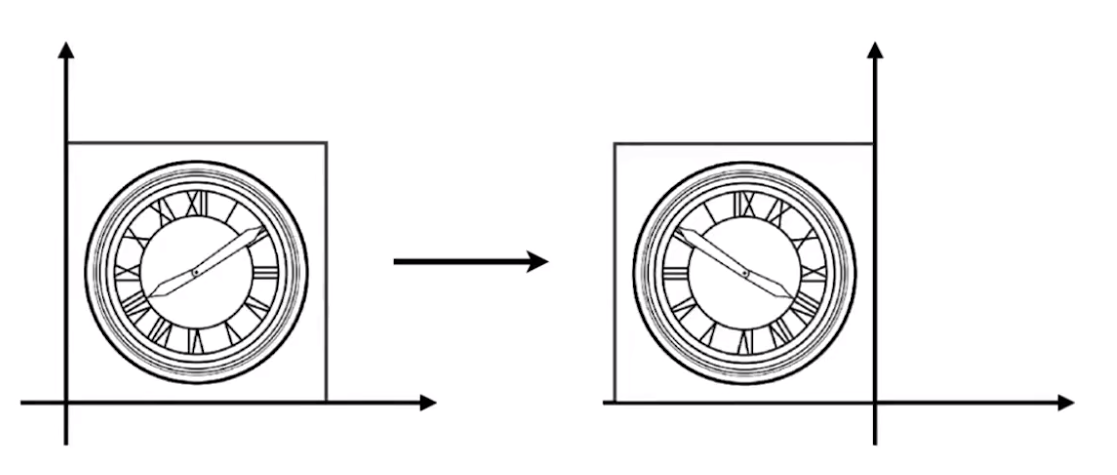
[x′y′]=[−1001][xy] \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} -1 & 0 \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} [x′y′]=[−1001][xy]
1.3 切变(Shearing)
把物体的其中一边固定,然后拉动对应的另外一边
shear−x(s)=[1s01]shear−y(s)=[10s1] \begin{aligned} shear-x(s) = \begin{bmatrix} 1 & s \\ 0 & 1 \end{bmatrix} \\[3ex] shear-y(s) = \begin{bmatrix} 1 & 0 \\ s & 1 \end{bmatrix} \end{aligned} shear−x(s)=[10s1]shear−y(s)=[1s01]
沿着 x 轴方向拉动 a 距离
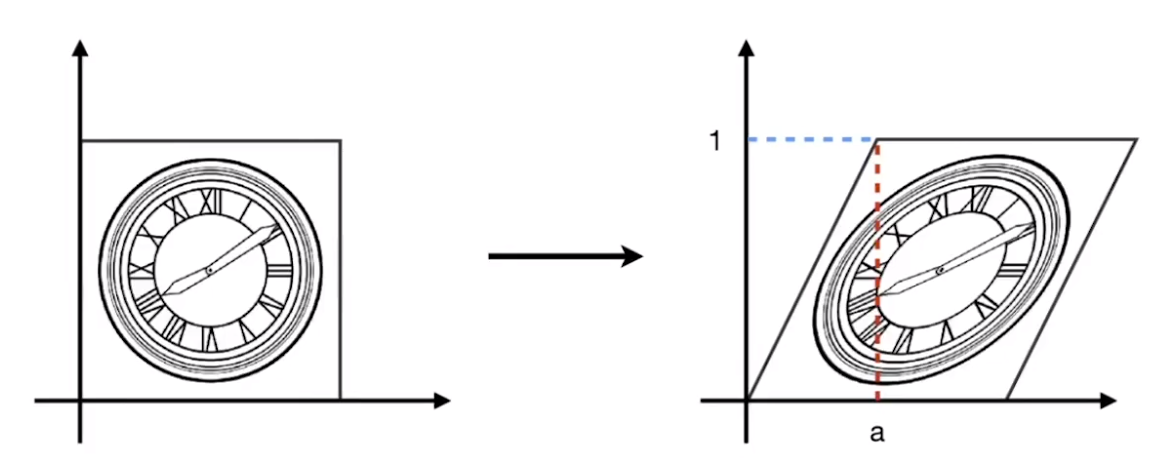
[x′y′]=[1a01][xy] \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} [x′y′]=[10a1][xy]
NOTE :
- 水平方向:x′=x+ayx' = x + ayx′=x+ay
- y = 0 的部分不变化
- y = 1 的部分右移 a 距离
- 竖直方向:y′=yy' = yy′=y
- 不变化
1.4 旋转
默认规定:
- 绕原点 (0,0)(0,0)(0,0) 进行旋转;
- 旋转方向为逆时针。
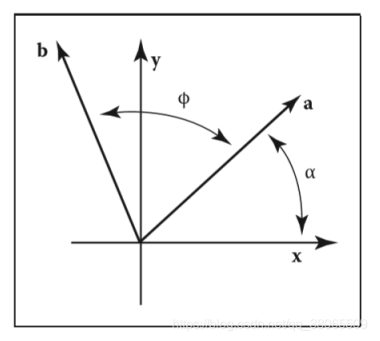
记为;
rotate(ϕ)=[cosϕ−sinϕsinϕcosϕ]
rotate(\phi) = \begin{bmatrix}
\cos\phi & -\sin\phi \\
\sin\phi & \cos\phi
\end{bmatrix}
rotate(ϕ)=[cosϕsinϕ−sinϕcosϕ]
可知:
{x′=xcosϕ−ysinϕy′=ycosϕ+xsinϕ \begin{cases} x' = x\cos\phi - y\sin\phi \\[1.5ex] y' = y\cos\phi + x\sin\phi \end{cases} ⎩⎨⎧x′=xcosϕ−ysinϕy′=ycosϕ+xsinϕ
即:
[x′y′]=[cosϕ−sinϕsinϕcosϕ][xy] \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \begin{array}{c:c} \cos\phi & -\sin\phi \\ \sin\phi & \cos\phi \end{array} \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} [x′y′]=[cosϕsinϕ−sinϕcosϕ][xy]
绕原点逆时针旋转 45°
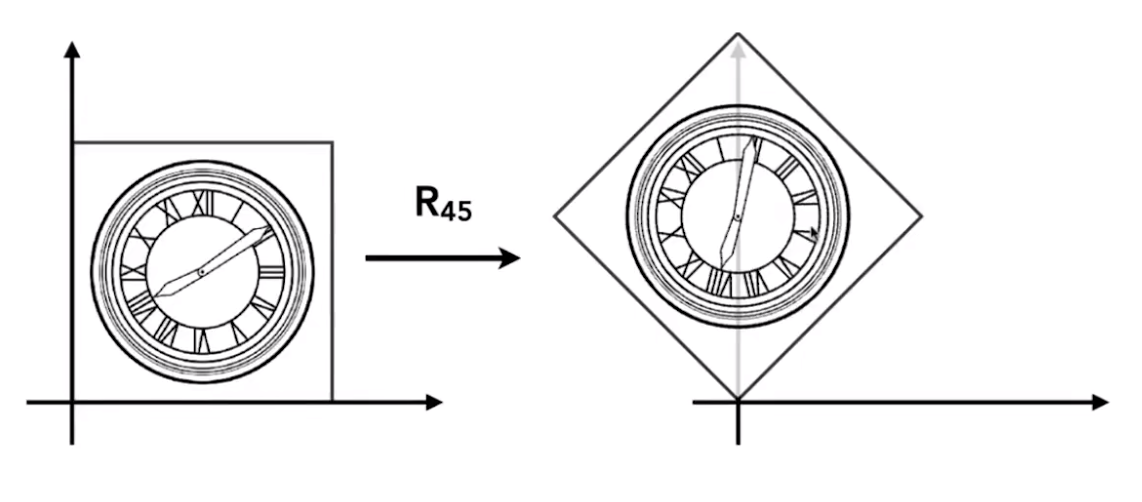
[22−222222] \begin{bmatrix} \cfrac{\sqrt{2}}{2} & -\cfrac{\sqrt{2}}{2} \\[3ex] \cfrac{\sqrt{2}}{2} & \cfrac{\sqrt{2}}{2} \end{bmatrix} ⎣⎢⎢⎢⎡2222−2222⎦⎥⎥⎥⎤
1.5 位移
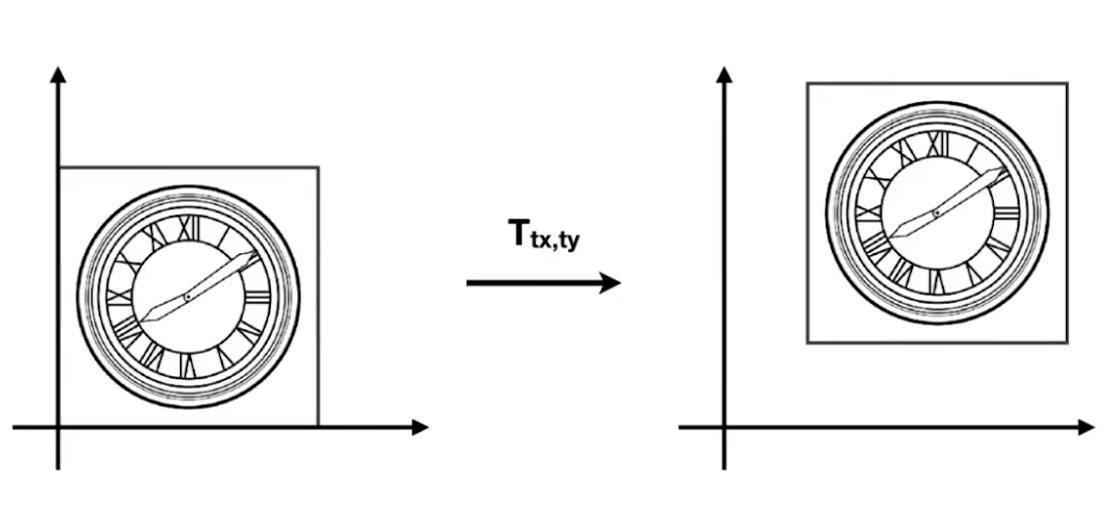
{x′=x+txy′=y+ty \begin{cases} x' = x + t_x \\ y' = y + t_y \end{cases} {x′=x+txy′=y+ty
但是当存在位移变换时,便无法仅靠一个二维矩阵的变换来进行表示:
[x′y′]=[abcd][xy]+[txty] \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix} [x′y′]=[acbd][xy]+[txty]
1.5.1 齐次坐标
增加一个维度,提供更多的信息,将二维向量区分为“点”和“位移向量”:
- 2D−point=(x,y,1)T2D-point = (x,y,1)^T2D−point=(x,y,1)T
- 2D−vector=(x,y,0)T2D-vector = (x,y,0)^T2D−vector=(x,y,0)T
使用的 1 和 0 是有实际意义的:
- vector + vector = vector(三角形法则:向量的叠加)
- point - point = vector(生成从第二个点指向第一个点的向量)
- point + vector = point(点进行位移)
- point + point = 这2个点的中点
可以通过三维空间中的一个点集去表示二维空间中的一个点
- 这个点集即是“视点”出发,穿过二维空间中“可视平面”上的该点的射线
- 射线点集 [xyw]\begin{bmatrix} x \\ y \\ w \end{bmatrix}⎣⎡xyw⎦⎤ 表示“可视平面”上的点 [x/wy/w1]\begin{bmatrix} x/w \\ y/w \\ 1 \end{bmatrix}⎣⎡x/wy/w1⎦⎤ ,w≠0w \ne 0w=0
此时可以使用矩阵变换去表示一个位移变换
- 当“点”进行位移时,会发生相应的变化:
[x′y′w′]=[10tx01ty001]⋅[xy1]=[x+txy+ty1] \begin{bmatrix} x' \\ y' \\ w' \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} x + t_x \\ y + t_y \\ 1 \end{bmatrix} ⎣⎡x′y′w′⎦⎤=⎣⎡100010txty1⎦⎤⋅⎣⎡xy1⎦⎤=⎣⎡x+txy+ty1⎦⎤
- 当“位移向量”进行位移时,不会发生变化:
[x′y′w′]=[10tx01ty001]⋅[xy0]=[xy0] \begin{bmatrix} x' \\ y' \\ w' \end{bmatrix} = \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 0 \end{bmatrix} = \begin{bmatrix} x \\ y \\ 0 \end{bmatrix} ⎣⎡x′y′w′⎦⎤=⎣⎡100010txty1⎦⎤⋅⎣⎡xy0⎦⎤=⎣⎡xy0⎦⎤
1.5.2 仿射变换
“线性变换” + “位移变换”
[x′y′]=[abcd]⋅[xy]+[txty] \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} a & b \\ c & d \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} t_x \\ t_y \end{bmatrix} [x′y′]=[acbd]⋅[xy]+[txty]
使用齐次坐标表示仿射变换:
[x′y′1]=[abtxcdty001]⋅[xy1] \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \begin{bmatrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} ⎣⎡x′y′1⎦⎤=⎣⎡ac0bd0txty1⎦⎤⋅⎣⎡xy1⎦⎤
NOTE:
- 仅在仿射变换下最后一排是 (0,0,1)(0,0,1)(0,0,1)
1.6 变换的组合
- 一个复杂变换可以拆分成若干个基础变换
- 变换顺序需要注意 —— 矩阵的乘法不满足交换律
R45⋅T(1,0)≠T(1,0)⋅R45 R_{45} \cdot T_{(1,0)} \ne T_{(1,0)} \cdot R_{45} R45⋅T(1,0)=T(1,0)⋅R45
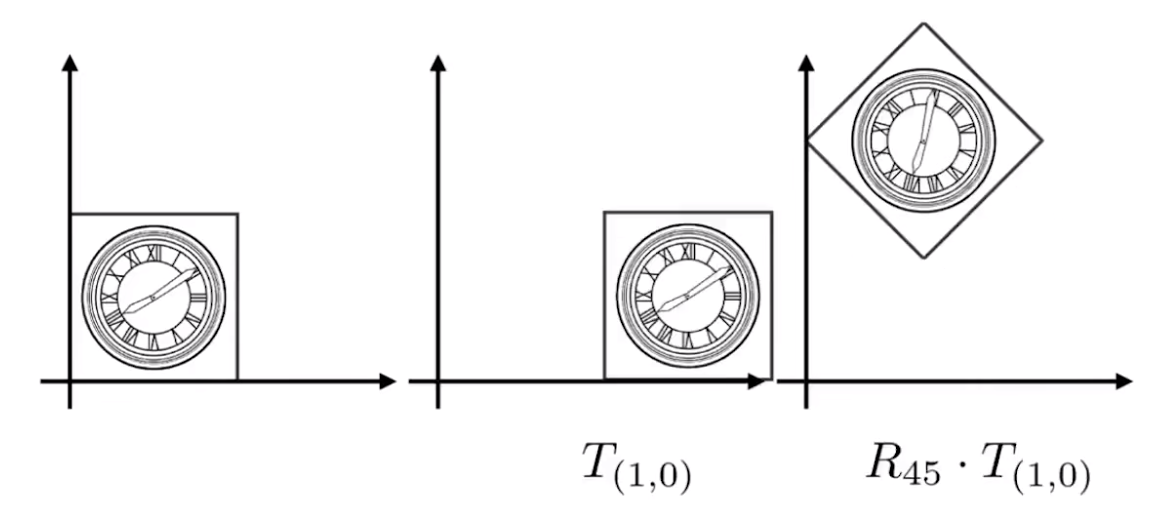
[x′y′1]=R45⋅T(1,0)⋅[xy1] \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = R_{45} \cdot T_{(1,0)} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} ⎣⎡x′y′1⎦⎤=R45⋅T(1,0)⋅⎣⎡xy1⎦⎤
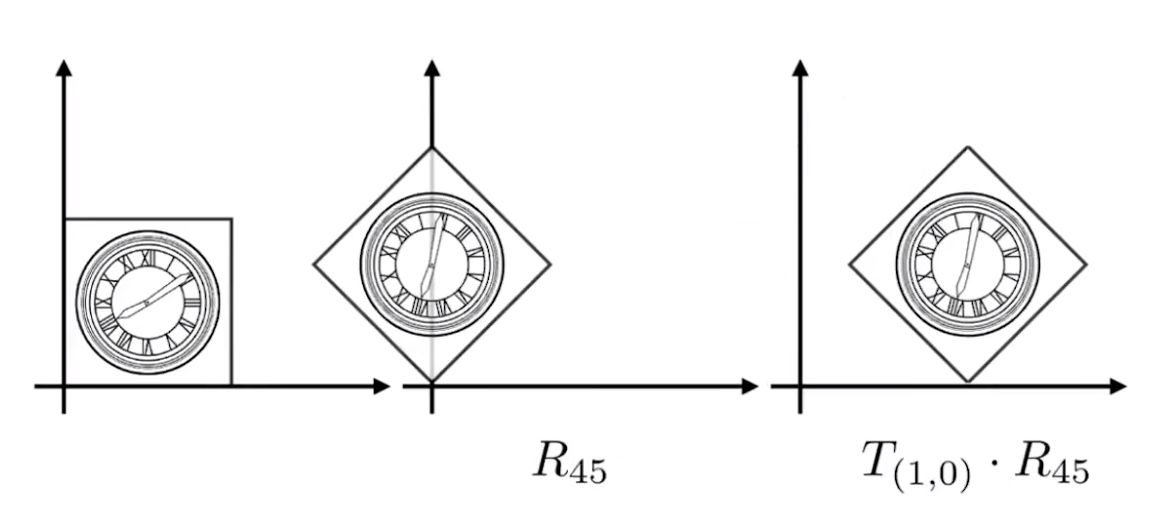
[x′y′1]=T(1,0)⋅R45⋅[xy1] \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = T_{(1,0)} \cdot R_{45} \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} ⎣⎡x′y′1⎦⎤=T(1,0)⋅R45⋅⎣⎡xy1⎦⎤
组合应用若干变换 A1,A2,A3,…A_1,A_2,A_3,\dotsA1,A2,A3,…
An(…A2(A1(x)))=An…A2⋅A1⋅[xy1] A_n(\dots A_2(A_1(x))) = A_n \dots A_2 \cdot A_1 \cdot \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} An(…A2(A1(x)))=An…A2⋅A1⋅⎣⎡xy1⎦⎤
NOTE :
矩阵有结合律,可以用一个矩阵表示这一系列的复合变换
2. 三维线性变换
2.1 仿射变换
-
3D−point=(x,y,z,1)T3D-point = (x,y,z,1)^T3D−point=(x,y,z,1)T
-
3D−vector=(x,y,z,0)T3D-vector = (x,y,z,0)^T3D−vector=(x,y,z,0)T
-
射线点集 [xyzw]\begin{bmatrix} x \\ y \\ z \\ w \end{bmatrix}⎣⎢⎢⎡xyzw⎦⎥⎥⎤ 表示“可视三维平面”上的点 [x/wy/wz/w1]\begin{bmatrix} x/w \\ y/w \\ z/w \\ 1 \end{bmatrix}⎣⎢⎢⎡x/wy/wz/w1⎦⎥⎥⎤ ,w≠0w \neq 0w=0
使用四维矩阵表示三维空间中的仿射变换
[x′y′z′1]=[abctxdeftyghitz0001]⋅[xyz1] \begin{bmatrix} x' \\ y' \\ z' \\ 1 \end{bmatrix} = \begin{bmatrix} a & b & c & t_x \\ d & e & f & t_y \\ g & h & i & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} ⎣⎢⎢⎡x′y′z′1⎦⎥⎥⎤=⎣⎢⎢⎡adg0beh0cfi0txtytz1⎦⎥⎥⎤⋅⎣⎢⎢⎡xyz1⎦⎥⎥⎤
2.2 缩放变换
Scale(sx,sy,sz)=[sx0000sy0000sz00001] Scale(s_x,s_y,s_z) = \begin{bmatrix} s_x & 0 & 0 & 0 \\ 0 & s_y & 0 & 0 \\ 0 & 0 & s_z & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} Scale(sx,sy,sz)=⎣⎢⎢⎡sx0000sy0000sz00001⎦⎥⎥⎤
2.3 位移变换
T(tx,ty,tz)=[100tx010ty001tz0001] T(t_x,t_y,t_z) = \begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix} T(tx,ty,tz)=⎣⎢⎢⎡100001000010txtytz1⎦⎥⎥⎤
2.4 旋转变换
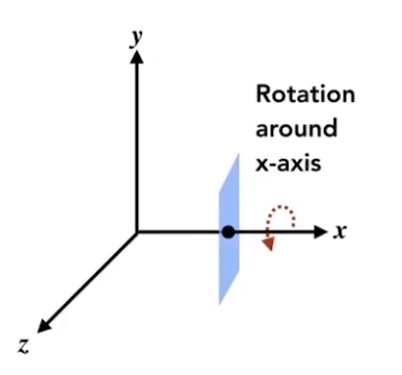
Rx(α)=[10000cosα−sinα00sinαcosα00001] R_x(\alpha) = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos{\alpha} & - \sin{\alpha} & 0 \\ 0 & \sin{\alpha} & \cos{\alpha} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} Rx(α)=⎣⎢⎢⎡10000cosαsinα00−sinαcosα00001⎦⎥⎥⎤
Ry(α)=[cosα0sinα00100−sinα0cosα00001] R_y(\alpha) = \begin{bmatrix} \cos{\alpha} & 0 & \sin{\alpha} & 0 \\ 0 & 1 & 0 & 0 \\ - \sin{\alpha} & 0 & \cos{\alpha} & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} Ry(α)=⎣⎢⎢⎡cosα0−sinα00100sinα0cosα00001⎦⎥⎥⎤
Rz(α)=[cosα−sinα00sinαcosα0000100001] R_z(\alpha) = \begin{bmatrix} \cos{\alpha} & - \sin{\alpha} & 0 & 0 \\ \sin{\alpha} & \cos{\alpha} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} Rz(α)=⎣⎢⎢⎡cosαsinα00−sinαcosα0000100001⎦⎥⎥⎤
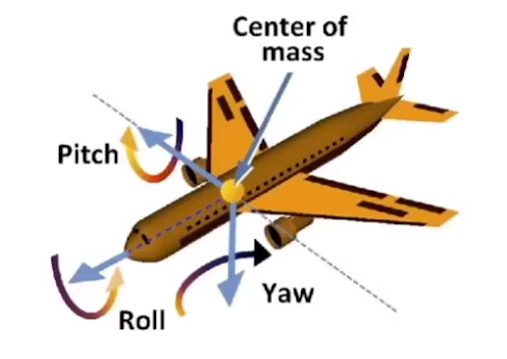
2.4.1 欧拉角
Rxyz(α,β,γ)=Rx(α)Ry(β)Rz(γ) R_{xyz}(\alpha,\beta,\gamma) = R_{x}(\alpha)R_{y}(\beta)R_{z}(\gamma) Rxyz(α,β,γ)=Rx(α)Ry(β)Rz(γ)
- 使用三个角:rollrollroll , pitchpitchpitch , yawyawyaw
2.4.2 罗德里格斯(Rodrigues)旋转方程
绕着某个过原点的轴 n\bold{n}n 旋转 α\alphaα 角度 :
R(n,α)=cos(α)I+(1−cos(α))nnT+sin(α)(0−nznynz0−nx−nynx0) \bold{R}(\bold{n},\alpha) = \cos(\alpha)\bold{I} + (1 - \cos(\alpha))\bold{n}\bold{n}^T + \sin(\alpha) \begin{pmatrix} 0 & -n_z & n_y \\ n_z & 0 & -n_x \\ -n_y & n_x & 0 \end{pmatrix} R(n,α)=cos(α)I+(1−cos(α))nnT+sin(α)⎝⎛0nz−ny−nz0nxny−nx0⎠⎞
式中的矩阵形式类似叉乘矩阵





 本文介绍了二维和三维空间中的线性变换原理,包括缩放、反射、切变、旋转和位移等基本变换,并详细解释了如何使用矩阵来表示这些变换。特别地,文章深入探讨了齐次坐标系下的仿射变换及其组合应用。
本文介绍了二维和三维空间中的线性变换原理,包括缩放、反射、切变、旋转和位移等基本变换,并详细解释了如何使用矩阵来表示这些变换。特别地,文章深入探讨了齐次坐标系下的仿射变换及其组合应用。
















 562
562

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








